HalfAdderandHalfSubtractorOperationsbyDNASelf-Assembly

160 浏览量 2021-02-21 11:43:44 上传评论收藏 1.02MB PDF 举报

资源推荐

资源详情

资源评论

RESEARCH ARTICLE

Printed in the United States of America

Journal of

Computational and Theoretical Nanoscience

Vol. 8, 1–8, 2011

Half Adder and Half Subtractor Operations by

DNA Self-Assembly

Yanfeng Wang

1 2 ∗

, Junwei Sun

, Xuncai Zhang

1 2

, and Guangzhao Cui

1 2

Research and Development Center of Biological Information Technology, Zhengzhou University of Light Industry,

Zhengzhou, 450002, China

College of Electrical and Electronic Engineering, Zhengzhou University of Light Industry,

Zhengzhou, 450002, China

Recently, experiments have demonstrated that the simple binary arithmetic and logical operations

can be executed by the process of self-assembly of DNA tiles. This paper brings out the realization

of the half adder and half subtractor using DNA self-assembly with parallel logical operations, in

much the way that a general-purpose computer can employ the simple logical circuits for a variety of

applications. The DNA self-assembly that we describe here are fundamentally the simple example,

but it seems possible to extend more complex logical circuits.

Keywords: DNA Self-Assembly, DNA Computation, Half Adder, Half Subtractor.

1. INTRODUCTION

In the past few decades, the traditional silicon-based com-

puter has made great contributions to the progress and

development of human society. But due to optical wave-

length limitations in conventional lithographic fabrication

techniques and physical limits, silicon-based technology

improvements will soon begin to approach their ultimate

limits in the rapidly approaching future. In the traditional

silicon-based computers, information processing in digi-

tal systems is straightforward and based on very simple

principles of Boolean logic. Logic gates are the devices

which are used to perform basic logical operations and

are the basis of the traditional silicon-based computer

processors, which perform logic and arithmetic opera-

tions between Boolean variables. Having a size more than

100 times smaller than the conventional silicon gates,

molecules offer excellent component minimization poten-

tial. The rapid emergence of DNA nanotechnology in

recent years has aroused much excitement among scien-

tists due to DNA self-assembly, as the most advanced and

versatile system, which has been experimentally demon-

strated for programmable construction of patterned sys-

tems on the molecular scale, and provides means to extend

Moore’s Law beyond the foreseen limits of small-scale

conventional silicon-based integrated circuits.

The notion of computation by interacting tiles dates

from Wang

in the 1960s. The use of stable branched DNA

∗

Author to whom correspondence should be addressed.

molecules containing sticky ends (DNA tiles) to produce

multidimensional constructs was proposed in the early

1980s.

Winfree

suggested using Wang tiles based on

branched DNA molecules to perform computation. Reif,

and Lagoudakis and LaBean

have made further sugges-

tions on this approach. The assembly of DNA-based tiles

into 2D periodic arrays has been reported several times

with a variety of motifs.

6–10

In addition, Rothemund

has

performed macroscopic-scale aperiodic self-assembly. In

2000, Mao et al. experimentally implemented the ﬁrst

algorithmic DNA self-assembly which performed a logi-

cal computation (cumulative XOR) on ﬁxed inputs.

2003, Yan et al. presented a novel cross shaped DNA

module (four-point–star motif), and formed square grid-

ding structure.

Subsequently, Yan et al. also demon-

strated parallel molecular XOR computation using DNA

tiling self-assembly in which a large number of distinct

inputs were simultaneously processed.

In 2005, He et al.

created 3-arm motifs called “3-point stars”, that crystallize

beautifully into 30-micron hexagonal lattices.

In 2008,

He et al. applied “3-point stars” to further assemble into

tetrahedron, dodecahedron and buckyball.

In 2010, Wang

et al. proposed the theoretical models to execute ﬁve steps

of a logical (cumulative AND and OR) operations on a

string of binary bits by using DNA triple-crossover (TX)

molecules.

Up to now, DNA nanotechnology based on

algorithmic self-assembly of DNA tiles had been devel-

oped at a high speed no matter in constructing theoretical

models or in building the complex nanoarchitectures.

J. Comput. Theor. Nanosci. 2011, Vol. 8, No. 7 1546-1955/2011/8/001/008 doi:10.1166/jctn.2011.1812 1

RESEARCH ARTICLE

Half Adder and Half Subtractor Operations by DNA Self-Assembly Wang et al.

In the traditional silicon-based digital computer, the

hardware circuit is consisted of the different kinds of log-

ical gates circuit, and digital logic circuit is the basis for

digital computer architecture. In a sense that molecular

logic gates built by DNA tiles could be considered as

the basic structure of a DNA computer. In this contribu-

tion, we present a theoretical model for the half adder

and half subtractor operations based on DNA algorithmic

self-assembly. The rest of this paper is structured as fol-

lows. We will brieﬂy review the basic deﬁnitions of the

half adder and half subtractor operations in Section 2, fol-

lowed by, in Section 3, the introduction of two kinds of

TX molecules which are employed in the following part.

We then formally describe the realization of the half adder

and half subtractor operations in Section 4, and ﬁnally we

will conclude in Section 5 with a summary discussion.

2. BASIC DEFINITIONS

2.1. Half Adder Operation

The half adder is a combinational logic unit performing

simple addition of two binary digits to produce two bits

as output, one bit for the Sum and other bit for the Carry.

The truth table for the half adder is shown in Table I.

Logic SUM represents the least signiﬁcant bit of the two

bits binary summation. Logic SUM is logic 0 when two

inputs are the same (two ones and two zeros), Otherwise,

it is logic 1. However, the other logic CARRY is logic 1

when both inputs have logic 1. Otherwise, it is logic 0.

Boolean functions that are derived from the truth table are

as follows.

SUM = A ⊕ B (1)

CARRY = A · B (2)

Boolean functions of logic SUM and logic CARRY

exactly coincide with the XOR gate and the AND gate.

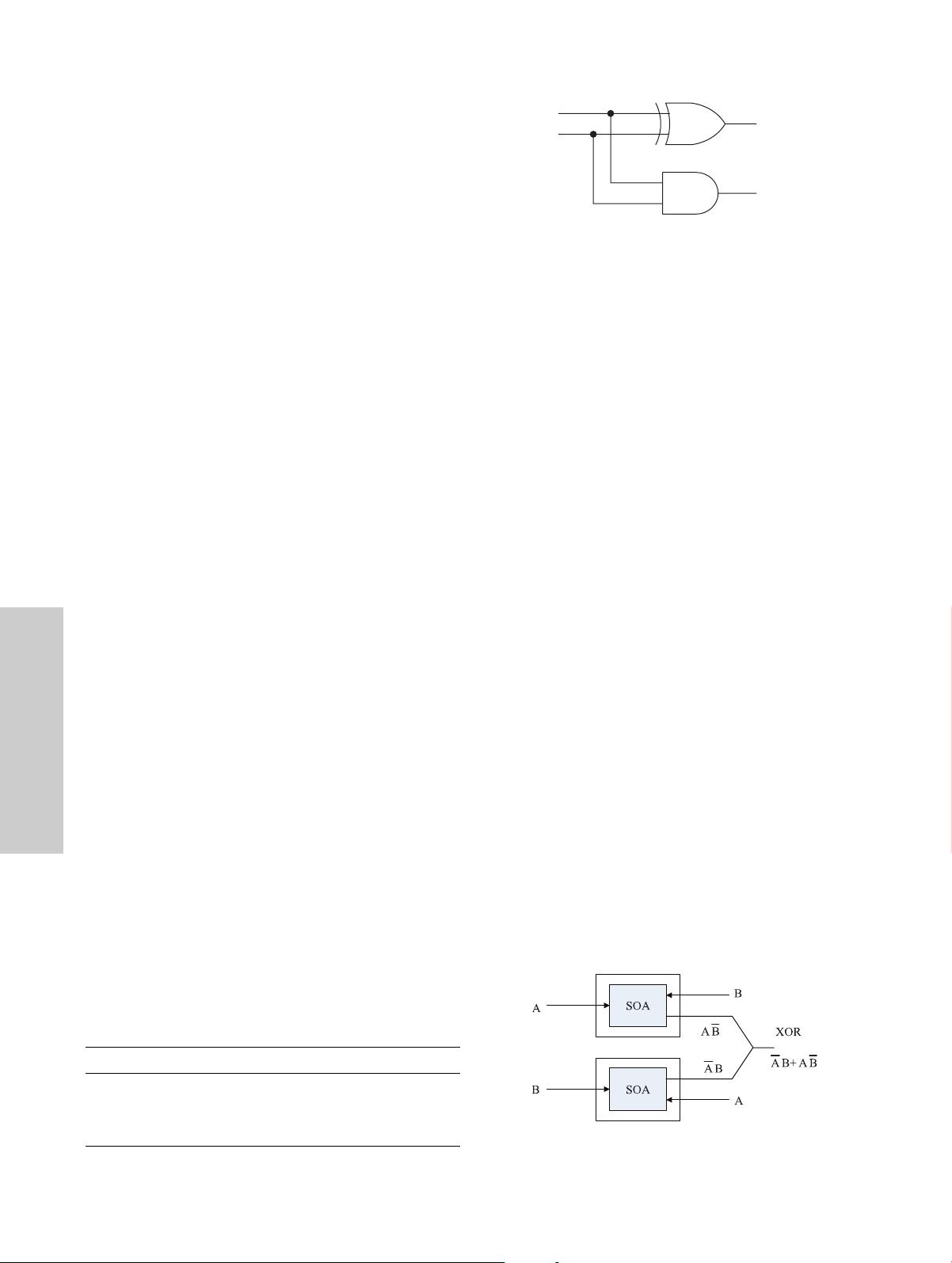
The structure of the half adder is shown in Figure 1. To

optically implement the proposed half adder, the all-optical

XOR and AND gates are employed.

Figure 2 shows the basic structure of the all-optical

XOR gate.

To implement the all-optical XOR gate, two

SOAs with cross-gain modulation (XGM) are used. In the

upper SOA, a probe signal A can not pass through it when

a strong pump signal B saturates its gain, while probe sig-

nal A simply passes through it in the absence of the strong

pump beam B. Thus, probe signal A passes through the

Table I. Truth table of half adder.

A B SUM CARRY

00 0 0

01 1 0

10 1 0

11 0 1

CARRY

SUM

XOR

AND

Fig. 1. Basic structure of half adder.

SOA only if the pump beam B is absent, and thus Boolean

B can be obtained. In the lower SOA, signals A and

B change their role and the output is given by Boolean

AB. Combining the two outputs of the SOAs, we obtain

Boolean A

B +

AB, which is Boolean-logically equal to A

XOR B yielding the complete all-optical XOR gate oper-

ation. These results are in accordance with the truth table

of logic SUM in Table I.

To implement the all-optical AND gate, binary charac-

teristics of the XPM wavelength converter are used.

using the static transfer characteristics of the XPM wave-

length converter with two distinctively different probe sig-

nal intensities shown in Figure 2, the all-optical logic AND

is realized. High power and low power of input signals can

be identiﬁed as logic 1 and 0, respectively. If the pump

signal is logic 0, the output is in position A regardless

of the probe signal intensity. Thus, output signal results

in logic 0. If the probe signal is logic 0, the output is in

either position A or B due to the pump signal inten-

sity. Thus, output signal also results in logic 0. When both

the probe and pump signals have the logic level of 1, the

output signal results logic 1 since it is located in posi-

tion C. These results are in accordance with the truth

table of logic CARRY in Table I.

A distinguished advantage of the half adder using this

scheme is that both the XOR gate and the AND gate only

depends on input signals A and B. Most of the previous

XOR and AND gates use additional input beam such as

clock signal or continuous wave (CW) light besides the

two input signal beams, and thus require additional light

sources.

Fig. 2. Scheme of all-optical XOR gate.

2 J. Comput. Theor. Nanosci. 8, 1–8, 2011

剩余7页未读，继续阅读

评论收藏

内容反馈

weixin_38722193

粉丝: 4
资源: 908

Half Adder and Half Subtractor Operations by DNA Self-Assembly

Full Adder and Full Subtractor Operations by DNA Self-Assembly

HA.rar_Half and Half_full adder_halfadder.hdl

szE-KP08-1-Half-Adder+and+Full-Adder.pdf

HA.rar_vhdl half adder

fulladder-using-half-adder.rar_full

Task1_WithCLK.rar_half adder

half_adder

FullAdder_4.rar_4 bit adder_half adder_全加器_四位全加器

half_adder_halfadder怎么用_半加器_vhdl_原理图_

generic_full_adder_and_subtractor:SystemVerilog中的通用全加法器和减法器

5- HALF ADDER.rar_行业发展研究_PDF__行业发展研究_PDF_

A 16-bit Carry Skip Adder Designed by Reversible Logic

binary_adder_subtractor.zip_subtracter

adder8_adder_full_

paypal Money Adder Generator v3.8 [07-09-2015].exe

All-optical logic gates and a half-adder based on lithium niobate photonic crystal micro-cavities

All-optical adder/subtractor based on terahertz optical asymmetric demultiplexer

Qt 5实现串口调试助手 （源工程文件、0积分下载）

【SystemVerilog】路科验证V2学习笔记（全600页）.pdf

AutoSAR标准协议4.2.2

光伏-储能并网系统仿真.rar

XCP协议的规范文档

GD32替换STM32注意事项.pdf

NPPJSONViewer.zip

蓝牙BLE协议中文版.pdf

CANoe通过CAPL脚本实现自动测试

AD20官方中文教程.pdf

最新资源

Qt 5实现串口调试助手（源工程文件、0积分下载）