QCD3对称破缺和味颤抖对偶性的推广资源-CSDN文库

Open

Access

9 浏览量 2020-04-05 12:08:57 上传评论收藏 1.44MB PDF 举报

资源推荐

资源详情

资源评论

JHEP02(2020)060

Published for SISSA by Springer

Received: August 21, 2019

Accepted: January 19, 2020

Published: February 11, 2020

Generalization of QCD

symmetry-breaking and

ﬂavored quiver dualities

Kyle Aitken,

Andrew Baumgartner,

Changha Choi

and Andreas Karch

Department of Physics, University of Washington,

Seattle, WA 98195-1560, U.S.A.

Physics and Astronomy Department, Stony Brook University,

Stony Brook, NY 11794-3800, U.S.A.

E-mail: kaitken17@gmail.com, baum4157@uw.edu,

changha.choi@stonybrook.edu, akarch@uw.edu

Abstract: We extend the recently proposed symmetry breaking scenario of QCD

the so-called “master” (2 + 1)d bosonization duality, which has bosonic and fermionic

matter on both ends. Using anomaly arguments, a phase diagram emerges with several

novel regions. We then construct 2+1 dimensional dualities for ﬂavored quivers using

node-by-node dualization. Such dualities are applicable to theories which live on domain

walls in QCD

-like theories with dynamical quarks. We also derive dualities for quivers

based on orthogonal and symplectic gauge groups. Lastly, we support the conjectured

dualities using holographic constructions, even though several aspects of this holographic

construction remain mostly qualitative.

Keywords: Duality in Gauge Field Theories, Topological Field Theories, Spontaneous

Symmetry Breaking, AdS-CFT Correspondence

ArXiv ePrint: 1906.08785

Open Access,

 The Authors.

Article funded by SCOAP

https://doi.org/10.1007/JHEP02(2020)060

JHEP02(2020)060

where we use “↔” to mean the two theories ﬂow to the same IR ﬁxed point. Since for each

of these dualities one side contains bosons and the other fermions, they are often referred

to as “3d bosonization” dualities.

It is not yet known how to rigorously show the aforementioned theories are dual, since

for a general choice of parameters they are strongly coupled. Nevertheless, there is growing

indication of their equivalence. Signiﬁcant evidence can be found in the large N and k

limit (with N/k ﬁxed) where observables such as the free energy, correlations functions,

and operator spectrum have been shown to match across both sides of the duality [2–8].

In the opposite limit when N = k = N

= 1, (1.1) can be used to derive an inﬁnite web

of dualities [9, 10] among which is the well-known bosonic particle-vortex [11, 12] and its

recently discovered fermionic equivalent [13]. Further checks come from anomaly matching

across the dualities [14], consistency on manifolds with boundaries [15, 16], deformations of

supersymmetric parents [17–19], explicit derivations of related systems from coupled 1 + 1

d wires [20], and Euclidean lattice constructions [21–24].

Another consistency check involves mass deforming each side of the duality. If the

mass deformation is large enough, one can integrate out the matter and explicitly show the

resulting topological ﬁeld theories (TFTs) are equivalent via level-rank duality, see ﬁgure 1.

However, this conﬁrmation breaks down when there are too many ﬂavors of matter. For

example, if N

> k then adding a large negative mass deformation for the scalar on the right

hand side of (1.1a) will completely break the gauge group resulting in a non-linear sigma

model. The corresponding mass deformation for the fermionic theory does not appear to

exhibit such a phase. Thus, the dualities in (1.1) were conjectured to only be valid when

they satisfy the inequality N

≤ k. We will refer to this as the “ﬂavor bound”.

More recently, a proposal has arisen for an extension of (1.1a) to the “ﬂavor-violated”

regime where k < N

< N

∗

(N, k) [25] where N

∗

is some undetermined upper bound. It

is conjectured that the fermionic side of (1.1a) also has a non-linear sigma model phase.

For light fermion mass, the fermions form a condensate and spontaneously break their

associated ﬂavor symmetry. This means both sides of the duality grow a quantum region

described by a complex Grassmannian, see ﬁgure 1. We will review the details of this

proposal in section 2.1.

Additionally, there has been an extension of the dualities (1.1) to include fermions and

bosons on both ends of the duality [26, 27],

SU(N)

−k+N

with N

ψ and N

φ ↔ U(k)

N−N

with N

Φ and N

Ψ. (1.2)

This is the so-called “master duality” since all known ﬂavor-bounded dualities are a special

case of said duality. Similar to (1.1), this duality is subject to a ﬂavor bound: the mass

deformations pass all checks so long as N

≤ N, N

≤ k, with the double saturated case

= N and N

= k excluded. Note (1.1a) and (1.1b) are simply the N

= 0 and N

= 0

limits of (1.2), respectively.

A natural next step is to combine the two aforementioned extensions of the 3d bosoniza-

tion dualities. As such, in the ﬁrst part of this paper we work to extend the master duality

to the ﬂavor-violated regime. Naively one may think this extension is fairly trivial and the

master duality grows a single new quantum region when fermion mass is light. However,

– 2 –

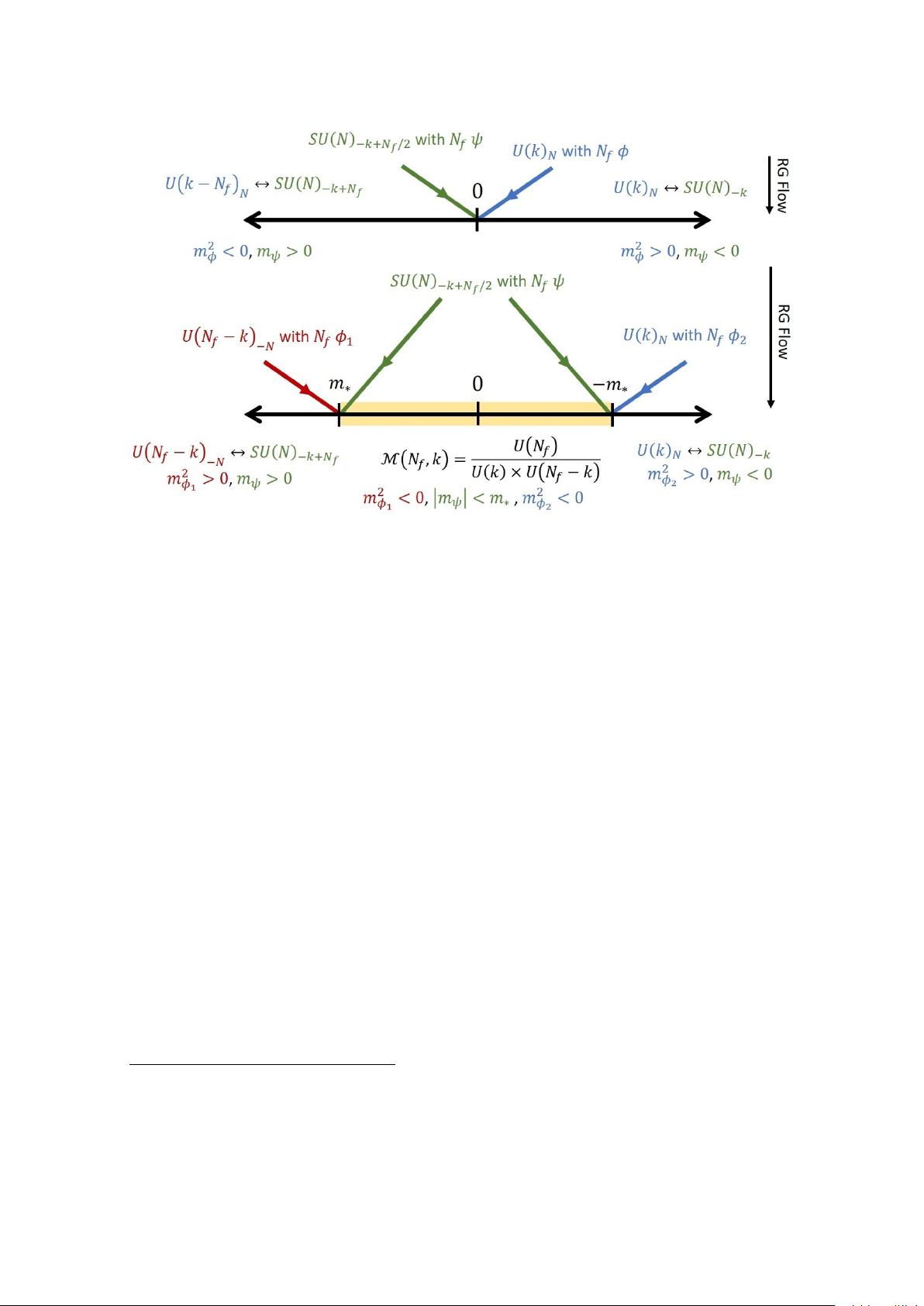
JHEP02(2020)060

Figure 2. Quiver gauge theory for the special case of n = 5 nodes. As usual, nodes denote gauge

groups and links denote bifundamental Wilson-Fisher scalars.

Other than simply performing the usual checks, i.e. agreement of massive phases and

anomalies, this duality was constructed using two diﬀerent approaches in [29]: ﬁrst, fol-

lowing the ideas developed in [30], the original quiver gauge theory was dualized “node-

by-node” using the master duality, (1.2). In general, such a procedure will yield a dual

quiver gauge theory with the same number of nodes. For the special case where the ranks

of the gauge group on all nodes were the same, N, the dual gauge theory had n − 1 con-

ﬁning nodes and so the only surviving gauge group was a single U(n)

factor, with the

bifundamental scalars being replaced with an adjoint “meson” ﬁeld. Secondly, the duality

was obtained from careful consideration of a holographic embedding of the duality [31].

One starts with the construction of ref. [28] that considered interfaces with varying theta

angle in four dimensional pure Yang-Mills theory. The TFTs which live on these domain

walls depends on the gradient of the theta angle — we get diﬀerent TFTs if the gradient

is “shallow” or “steep”. If the transition between these two regimes is second order, the

corresponding ﬁxed point should be governed by the quiver conformal ﬁeld theory (1.3).

The holographic dual of such interfaces is well known [32] in the context of the simplest

holographic dual for a conﬁning gauge theory, Witten’s black hole [33]. The key point is

that the holographic dual at low energies does not give back the quiver gauge theory (1.3),

but its dual incarnation (1.4).

Both of these techniques can be employed in order to derive more general dualities

in the same spirit, even though the holographic construction proves to require a certain

amount of additional assumptions. One thing we do in this work is to include fundamental

ﬂavors. In [28] domain walls in QCD

were considered not just for the case of N

= 0 (i.e.

pure YM), but also for the cases N

= 1 and N

> 1, which appear somewhat distinct.

The quiver theory described above gets augmented with extra fundamental matter on each

node (see ﬁgure 7). Once more, we can derive a dual via node-by-node dualization. We will

see the N

> 1 and N

= 1 cases require use of two distinct regimes of the ﬂavor-violated

master duality we propose in the ﬁrst part of this paper.

Holographically, the inclusion of ﬂavor can be accomplished by adding probe D8 and

D8 branes as in the Sakai-Sugimoto model [34]. Holographic theta walls in this context

have been discussed recently in [35]. While both constructions have their own subtleties,

in the end both give closely related conjectured duals for ﬂavored quivers.

A second generalization is to extend the original construction to gauge theories based

on orthogonal and symplectic groups. The master duality is known for these gauge groups

as well, so once more we can employ a node-by-node dualization. On the holographic side,

the projection to orthogonal and symplectic groups can be enforced by orientifolds. Again

we see consistency between the node-by-node dualization and the holographic construction.

– 4 –

剩余42页未读，继续阅读

评论收藏

内容反馈

weixin_38716423

粉丝: 4
资源: 928

QCD3对称破缺和味颤抖对偶性的推广

关于三维量子场论中的对偶性的讨论

SU（3）QCD的阿贝尔分解和Weyl对称有效作用

QCD3对偶与F定理

具有电弱对称性和QCD手性对称性破坏的dS沼泽猜想

QCD振幅的运动学对偶

手性QCD中对称性断裂的模式

QCD3的对称破例

大数据-算法-约束系统的正则Ward恒等式及其在动力学对称性破缺中的应用.pdf

大N超对称QCD中的θ和η'

伴随QCD4，限定的临界现象，富含对称性的拓扑量子场论和更高的对称性扩展

QCD的共形对称性

两个伴随QCD3和一个对偶链的阶段

具有约束夸张和动态大胶子的模型中具有大量夸克的QCD手性对称修复

从摄动角度看超对称规范理论的对偶

QCD状态方程和轻子不对称性对原始引力波的影响

全息QCD中的共形对称性破坏

对齐QCD轴的Peccei-Quinn对称性的质量及其宇宙学意义

高温QCD中的U（1）轴对称性和Dirac光谱

QCD中的过度渐近和夸克强子对偶违规

类型0弦和Seiberg对偶的U（N c）QCD3相

晶格QCD的Kaon分布幅度和风味SU（3）对称性

在有效模型框架下具有手性和同位旋不平衡的稠密夸克物质的对偶性和不均匀相

大型Nc超对称QCD中的动力学超对称破坏

Z3-QCD模型中不同中心对称破坏模式的Roberge-Weiss跃迁

全息QCD研究的手性相和限定性相变

QCD硬散射中的方位角不对称：红外安全但发散

软破碎超对称QCD中的畴壁和CP异常

最新资源