Verlinde引力的引力微透镜资源-CSDN文库

Open

Access

77 浏览量 2020-05-05 10:35:58 上传评论收藏 373KB PDF 举报

资源推荐

资源详情

资源评论

Physics Letters B 769 (2017) 281–288

Contents lists available at ScienceDirect

Physics Letters B

www.elsevier.com/locate/physletb

Gravitational microlensing in Verlinde’s emergent gravity

Lei-Hua Liu

∗

, Tomislav Prokopec

Institute for Theoretical Physics, Spinoza Institute and the Center for Extreme Matter and Emergent Phenomena (EMME), Utrecht University,

Buys

Ballot Building, Princetonplein 5, 3584 CC Utrecht, The Netherlands

a r t i c l e i n f o a b s t r a c t

Article history:

Received

6 December 2016

Received

in revised form 29 March 2017

Accepted

29 March 2017

Available

online 31 March 2017

Editor:

M. Trodden

We propose gravitational microlensing as a way of testing the emergent gravity theory recently proposed

by Eric Verlinde [1]. We consider two limiting cases: the dark mass of maximally anisotropic pressures

(Case I) and of isotropic pressures (Case II). Our analysis of perihelion advancement of a planet shows

that only Case I yields a viable theory. In this case the metric outside a star of mass M

∗

can be modeled

by that of a point-like global monopole whose mass is M

∗

and a deﬁcit angle  =



(2GH

∗

)/(3c

where H

is the Hubble rate and G the Newton constant. This deﬁcit angle can be used to test the theory

since light exhibits additional bending around stars given by, α

≈−π/2. This angle is independent on

the distance from the star and it affects equally light and massive particles. The effect is too small to be

measurable today, but should be within reach of the next generation of high resolution telescopes. Finally

we note that the advancement of periastron of a planet orbiting around a star or black hole, which equals

π per period, can be also used to test the theory.

(http://creativecommons.org/licenses/by/4.0/). Funded by SCOAP

1. Global monopole metric

In a recent paper Eric Verlinde [1] has proposed a novel emer-

gent

gravity theory. The most important claim of the theory is that

dark matter has no particle origin but instead it is an emergent

manifestation in modiﬁed gravity. Assuming spherical symmetry

Verlinde obtains,





)



(r)r

, (1)

where H

= 2.36 × 10

−18

−1



√

/3is the current Hub-

ble

parameter,  is the cosmological constant (whose value is

determined by the current dark energy density), G = 6.674 ×

−11

/(kg s

) is the Newton’s constant, c ≈3 ×10

m/sis the

speed of light, M

(r) (M

(r)) is the baryonic mass (dark mass)

inside a sphere of radius r.

Eq. (1) implies that for a star of uniform density ρ

∗

, M

∗

4π

∗

, inside the star,

(r) =



2cH

∗

3GR

∗

∝r

5/2

, r < R

∗

, (2)

Corresponding author.

E-mail

addresses: L.Liu1@uu.nl (L.-H. Liu), t.prokopec@uu.nl (T. Prokopec).

where R

∗

denotes star’s radius. On the other hand, outside the star,

∝r, and we have,

(r) =



∗

×r , r ≥ R

∗

. (3)

The main goal of this paper is to construct the metric tensor

that consistently incorporates (1) within the Verlinde’s emergent

gravity theory and to investigate how that metric can be used to

test the theory. The fundamental assumption we make is that the

theory admits metric formulation that can be obtained by solv-

ing

suitably modiﬁed Einstein’s equations (23). In the Appendix we

perform a detailed analysis of such a theory. Unfortunately, we do

not have all of the information needed to fully specify the metric.

A reasonable assumption is that the modiﬁed stress energy tensor

is diagonal, T

=diag[−ρ, P

, P

], see (24). In the weak grav-

itational

ﬁeld regime (which is of our principal concern here) that

should be justiﬁed. This leaves us with four unknown functions:

energy density ρ (which we can determine from (1)) and three un-

known

pressures: P

, P

. For spherically symmetric mass dis-

tribution

the two angular pressures must be equal, P

= P

≡ P

⊥

The remaining pressures are unknown, but are nevertheless tightly

constrained by the TOV equation (41), however not enough to be

completely speciﬁable. Rather than attempting to extend Verlin-

de’s

theory to obtain a relationship between the energy density

and pressures, here we consider two simple and plausible Ansätze:

http://dx.doi.org/10.1016/j.physletb.2017.03.061

0370-2693/

282 L.-H. Liu, T. Prokopec / Physics Letters B 769 (2017) 281–288

Case I: Field-like dark mass: P

⊥

=0;

Case

II: Particle-like dark mass: P

⊥

= P

≡ P .

addition, in Case II, we assume that inside a star (where except

at very small radii baryonic contribution dominates) baryonic mat-

ter

is non-relativistic, and hence P

ρ

, implying also P  ρ.

The

extensive analysis in the Appendix (cf. Eqs. (39), (50) and

(67)) shows that the metric tensor is of the form,

=−



1 − −

1 − w



−

2GM

∗







(1+w



)

1 − −

−

2GM

∗

d

, (4)

where d 

= dθ

+ sin

(θ)dϕ

is the metric of the two-dimensi-

onal

unit sphere (θ ∈[0, π], ϕ ∈[0, 2π)), w



= P /ρ =−1is the

equation of state parameter for Case I (P

= P , P

⊥

=0) and w



for

Case II (P

= P = P

⊥

). This then implies that outside the star

for Case I the metric can be written as that of a point-like global

monopole on de Sitter background,

and  is the deﬁcit solid an-

gle

deﬁned by,

 =



2GH

∗

. (5)

That  in (5) indeed represents a deﬁcit solid angle that cannot be

removed by a coordinate transformation can be shown as follows.

Observe ﬁrstly that the volume (surface area) of a two sphere of

radius r is (S

(r)) =4πr

, which deﬁnes the coordinate r (these

coordinates are similar to those used in the Schwarzschild metric).

Now, one can try to remove  by the following coordinate trans-

formations,

r =

√

1 −

t =(1 −)

[1+(1+w



)]

×t ,

(

1 −)d



(6)

after which  seems to disappear from the metric (4). Indeed, the

equivalent metric is,

=−



1 −

1 − w



−

∗







(1+w



)

1 −

−

∗



, (7)

where

∗

(1 −)

3/2

. (8)

However,  does not entirely disappear since in the new coordi-

nates,



+sin



√

1 −



(9)

Global monopoles are topological solutions of classical equations of motion of

a scalar ﬁeld theory with 3real scalar ﬁelds,



 = (

, 

)

whose Lagrangian

is O (3) symmetric and whose potential exhibits a spontaneous symmetry break-

ing,

V (



) =(λ/4)(







 −

)

. One can show that in this case the solution with

topological charge 1 [2] will backreact on the metric such to induce a solid deﬁcit

angle,  =8π G

(c =1), see e.g. [3,4]. From the gravitational point of view com-

pact

star-like dense objects (black hole mimickers) built out of topologically charged

scalar matter [5] resemble ordinary stars in Verlinde’s theory.

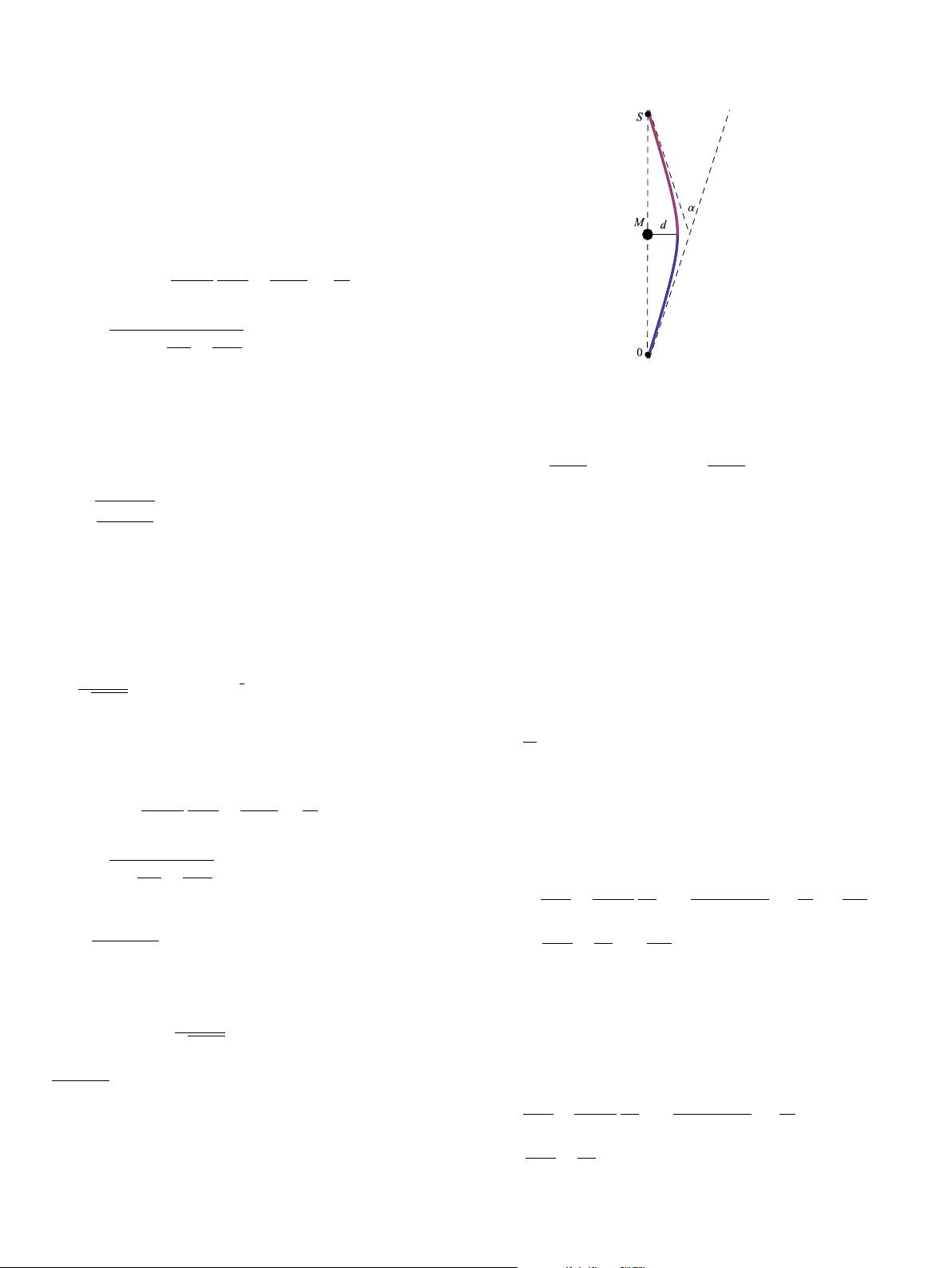
Fig. 1 . Light deﬂection around a star of mass M

∗

= M. The closest distance to the

center of the star is d. The deﬂection angle α can be calculated by integrating (12)

along

the path of light from the source S to the observer O .

and

ϕ and

take values in the intervals,

θ ∈[

0, π

√

1 − ],

ϕ ∈[0, 2π

√

1 −). (10)

It is an easy exercise to calculate the surface area of the two di-

mensional

sphere of radius

r in these new coordinates,

(S

(

r)) =4π(1 −)

. (11)

From this result it is obvious that the sphere contains a solid an-

gle

deﬁcit of, δ =−4π, completing the proof. In the following

section we discuss the physical signiﬁcance of this result.

2. Gravitational lensing

In this section we consider the lensing in a metric given by (4)

and (7).

The usual weak (linearized) lensing formula for the deﬂec-

tion

angle (in radians),

α =−



∇

⊥



φ(



x) +ψ(



d, (12)

where  is the path along the light geodesic (from the source to

the observer, see Fig. 1), ∇

⊥

is the gradient operator in the plane

orthogonal to the propagation of light and φ and ψ are the two

gravitational potentials (corresponding to the g

and g

metric

perturbations). Outside the star these potentials can be read off

from (4),

φ(r) =−

∗

−

1 − w



(1 + w



)





−



ψ(

r) =−

∗

−



. (13)

The lensing formula (12) can be used for the ﬁrst three parts of

the potential (the one induced by the star mass, by the Universe’s

expansion and the logarithmic piece), but it cannot be used for the

constant contribution, φ

=−c

/2, from the dark mass simply

because, ∇

⊥

= 0(how to calculate light deﬂection due to φ

is discussed below). For that reason it is better to use the second

form of the metric (7), in which case the gravitational potential is,

φ =−

∗

−

1 − w



(1 + w



)





ψ =−

∗

−

(14)

Inserting this into (12) gives for the lensing angle,

剩余7页未读，继续阅读

评论收藏

内容反馈

weixin_38710198

粉丝: 6
资源: 912

Verlinde引力的引力微透镜

熵引力的彩虹引力修正

常规黑洞的Cardy-Verlinde公式及其自重校正

论文研究 - 引力，暗能量和暗物质基本性质的线索

拓扑顺序中边缘激励的缺陷Verlinde公式

论文研究 - 平面空间宇宙学作为Penrose的Weyl曲率假说和引力熵的模型

对数（p +，p−）-模型的模转换和Verlinde公式

论文研究 - 潜在有用的银河暗物质指数

来自（非）全息屏幕的暗重力

Jackiw-Teitelboim量子引力的缺陷

Kachru-Pearson-Verlinde真空衰减中的重整催化

线缺陷Schur指数，Verlinde代数和U（1）r不动点

全息屏幕上晚宇宙中出现的暗物质

henkverlinde.com：Henk Verlinde网站

弯曲空间上的N = 4超对称力学

Qt 5实现串口调试助手 （源工程文件、0积分下载）

【SystemVerilog】路科验证V2学习笔记（全600页）.pdf

AutoSAR标准协议4.2.2

光伏-储能并网系统仿真.rar

XCP协议的规范文档

GD32替换STM32注意事项.pdf

NPPJSONViewer.zip

蓝牙BLE协议中文版.pdf

CANoe通过CAPL脚本实现自动测试

AD20官方中文教程.pdf

最新资源

Qt 5实现串口调试助手（源工程文件、0积分下载）