没有合适的资源?快使用搜索试试~ 我知道了~
Event-triggered controller design of nonlinear discrete-time net...
0 下载量 8 浏览量
2021-02-10
22:54:27
上传
评论
收藏 853KB PDF 举报
温馨提示
This article is concerned with event-triggered fuzzy control design for a class of discrete-time nonlinear networked control systems (NCSs) with time-varying communication delays. Firstly, a more general mixed event-triggering scheme (ETS) is proposed. Secondly, considering the effects of the ETS and communication delays, based on the T-S fuzzy model scheme and time delay system approach, the original nonlinear NCSs is reformulated as a new event-triggered networked T-S fuzzy systems with interv
资源推荐
资源详情
资源评论

Applied
Soft
Computing
30
(2015)
400–411
Contents
lists
available
at
ScienceDirect
Applied
Soft
Computing
j
ourna
l
ho
me
page:
www.elsevier.com/locate
/asoc
Event-triggered
controller
design
of
nonlinear
discrete-time
networked
control
systems
in
T-S
fuzzy
model
Songlin
Hu
a,b
,
Dong
Yue
b,∗
,
Chen
Peng
c
,
Xiangpeng
Xie
b
,
Xiuxia
Yin
d
a
College
of
Automation,
Nanjing
University
of
Posts
and
Telecommunications,
Nanjing
210023,
PR
China
b
Institute
of
Advanced
Technology,
Nanjing
University
of
Posts
and
Telecommunications,
Nanjing
210023,
PR
China
c
School
of
Mechatronic
Engineering
and
Automation,
Shanghai
University,
Shanghai
200072,
PR
China
d
Department
of
Mathematics,
School
of
Science,
Nanchang
University,
Nanchang,
Jiangxi
330031,
PR
China
a
r
t
i
c
l
e
i
n
f
o
Article
history:
Received
10
April
2012
Received
in
revised
form
18
November
2014
Accepted
23
January
2015
Available
online
2
February
2015
Keywords:
Networked
control
systems
Takagi-Sugeno
(T-S)
fuzzy
model
Event-triggered
communication
scheme
Communication
delays
Co-design
algorithm
a
b
s
t
r
a
c
t
This
article
is
concerned
with
event-triggered
fuzzy
control
design
for
a
class
of
discrete-time
nonlin-
ear
networked
control
systems
(NCSs)
with
time-varying
communication
delays.
Firstly,
a
more
general
mixed
event-triggering
scheme
(ETS)
is
proposed.
Secondly,
considering
the
effects
of
the
ETS
and
com-
munication
delays,
based
on
the
T-S
fuzzy
model
scheme
and
time
delay
system
approach,
the
original
nonlinear
NCSs
is
reformulated
as
a
new
event-triggered
networked
T-S
fuzzy
systems
with
interval
time-varying
delays.
Sufficient
conditions
for
uniform
ultimately
bound
(UUB)
stability
are
established
in
terms
of
linear
matrix
inequalities
(LMIs).
In
particular,
the
quantitative
relation
between
the
bound-
ness
of
the
stability
region
and
the
triggering
parameters
are
studied
in
detail.
Thirdly,
a
relative
ETS
is
also
provided,
which
can
be
seen
as
a
special
case
of
the
above
proposed
mixed
ETS.
As
a
difference
from
the
preceding
results,
sufficient
conditions
on
the
existence
of
desired
fuzzy
controller
are
derived
to
ensure
the
asymptotic
stability
of
the
closed-loop
system
with
reduced
communication
frequency
between
sensors
and
controllers.
Moreover,
a
co-design
algorithm
for
simultaneously
determining
the
gain
matrices
of
the
fuzzy
controller
and
the
triggering
parameters
is
developed.
Finally,
two
illustrative
examples
are
presented
to
demonstrate
the
advantage
of
the
proposed
ETS
and
the
effectiveness
of
the
controller
design
method.
©
2015
Elsevier
B.V.
All
rights
reserved.
1.
Introduction
Control
systems
in
which
the
different
components
(i.e.,
sensors,
controllers,
and
actuators)
are
physically
distributed
at
differ-
ent
locations
and
connected
through
a
shared
communication
networks
are
called
networked
control
systems
(NCSs).
Low
cost,
easy
maintenance,
and
system
flexibility
have
dramatically
stim-
ulated
the
use
of
wired
or
wireless
shared
networks
in
a
great
number
of
real
world
applications,
for
example,
sensor
networks,
remote
surgery,
and
intelligent
transportation
systems
[17].
How-
ever,
although
NCSs
have
a
distinct
advantage
over
the
tranditional
point-to-point
control
systems,
the
introduction
of
communica-
tion
networks
in
control
loops
brings
some
challenging
problems
such
as
network-induced
delays
and/or
packet
dropouts,
which
may
degrade
system
performance
or
even
cause
instability
[58].
In
the
past
decade,
how
to
deal
with
these
typical
issues
in
NCSs
∗
Corresponding
author.
E-mail
address:
medongy@vip.163.com
(D.
Yue).
has
become
an
active
research
area,
and
a
number
of
important
results
on
modeling,
control,
and
opimization
of
NCSs
have
been
reported
in
the
existing
literature.
According
to
the
controlled
plants
in
the
published
work,
the
results
can
be
simply
classi-
fied
into
two
types:
some
results
are
focus
on
linear
NCSs,
see,
for
example,
[11,12,30,35,41,42,45–49,52,57];
others
are
for
non-
linear
NCSs,
see,
for
example,
[5,8,13,16,18,23,40,54,55].
It
should
be
pointed
out,
however,
that
these
pieces
of
work
are
based
on
a
common
assumption
that
the
sensor
is
time-triggered
(or
periodic-
triggered),
which
implies
that
all
the
sensor
measurement
need
to
be
transmitted
to
controller
through
communication
networks
at
a
fixed
rate
regardless
of
the
state
of
the
system
to
be
controlled
[32].
In
fact,
in
some
cases,
there
is
no
need
to
transmit
the
measurement
signal
to
controller
node
for
computation,
see,
for
example,
when
the
states
of
the
controlled
plant
are
close
to
equilibrium
point,
since
the
effect
of
the
sensor
measurement
signal
on
system
per-
formance
become
small
during
the
steady
stage
of
state.
Therefore,
in
the
time-triggered
transmission
framework,
some
redundant
measurement
signal
may
be
transmitted,
which
leads
to
inefficient
utilization
of
the
limited
network
resources.
http://dx.doi.org/10.1016/j.asoc.2015.01.041
1568-4946/©
2015
Elsevier
B.V.
All
rights
reserved.
S.
Hu
et
al.
/
Applied
Soft
Computing
30
(2015)
400–411
401
In
order
to
save
the
network
bandwidth
utilization
while
main-
taining
the
stability
and
a
level
of
performance
of
the
NCSs,
an
intuitive
way
is
to
reduce
the
transmission
of
the
sensor
mea-
surement
signal
as
much
as
possible.
To
this
end,
a
so-called
event-triggered
transmission
scheme,
also
called
event-based
transmission
scheme
has
been
proposed
in
the
open
literature.
As
an
alternative
to
the
time-triggered
transmission
scheme,
event-
triggered
transmission
scheme
arises
for
its
great
benefits
in
saving
communication
resources
[37].
In
the
event-triggered
transmission
framework,
whether
or
not
the
sensor
measurement
signal
should
be
transmitted
is
determined
by
the
occurrence
of
an
“event”
rather
than
“time”.
Since
the
pioneering
work
[1]
on
event-based
con-
trol,
several
different
ETSs
have
been
proposed
for
different
system
models.
To
name
a
few,
an
absolute
ETS
for
linear
NCSs,
see,
for
example,
[21,27,28,56];
a
relative
ETS
for
linear
NCSs,
see,
for
exam-
ple,
[6,7,9,10,14,15,24,31,33,53];
a
relative
ETS
for
nonlinear
NCSs,
see,
for
example,
[17,32,44].
It
is
worth
noting
that,
although
the
above
mentioned
the-
oretical
results
on
event-triggered
linear
or
nonlinear
NCSs
are
rich,
the
existing
results
are
still
limited
and
there
still
exist
some
issues
to
be
worthy
of
further
investigatation
due
to
the
facts
that:
(i)
most
of
the
aforementioned
ETSs
have
been
per-
formed
in
the
continuous-time
linear
NCSs
framewok.
As
is
known,
network-based
communications
are
inherently
of
discrete
nature,
as
packet-based
protocols
are
commonly
used
to
connect
the
components
of
the
NCSs,
not
allowing
for
a
continuous
flow
of
information
in
the
classic
way.
Despite
this
fact,
little
attention
has
been
paid
to
discrete-time
NCSs
in
the
literature,
especially
to
the
discrete-time
nonlinear
NCSs
due
to
the
systems’
complex-
ity.
Therefore,
it
is
preferable
to
design
a
new
ETS
for
discrete-time
nonlinear
NCSs;
(ii)
most
of
the
above
mentioned
results
are
based
on
the
Lyapunov
stability
of
the
considered
NCSs.
Notice
that
sta-
bility
in
the
sense
of
Lyapunov
requires
the
ability
to
keep
the
state
arbitrarily
close
to
the
system
equilibrium
as
long
as
the
initial
state
is
close
enough
to
it.
This
is
a
strong
requirement
for
prac-
tical
systems
operating
in
the
presence
of
unknown
disturbances.
As
stated
in
[19],
asymptotic
stability
is
generally
not
possible
but
the
ultimate
boundness
of
the
systems’s
state
can
be
achieved
in
the
presence
of
such
perturbations.
Unfortunately,
very
few
results
related
to
ultimate
boundness
of
the
systems’s
state
in
event-
triggered
discrete-time
NCSs
have
been
available
in
the
literature
so
far.
Even
though
the
ultimately
bounded
stability
in
event-
triggered
feedback
control
system
has
been
discussed
in
[22,27,28],
the
co-design
for
feedback
gain
matrix
and
ETS
cannot
be
realized
in
[22],
and
in
[27,28],
only
discrete-time
linear
NCSs
rather
than
discrete-time
nonlinear
NCSs
is
considered.
Hence,
it
is
significant
and
necessity
to
study
the
event-triggered
controller
design
for
discrete-time
nonlinear
NCSs
with
taking
ultimate
boundness
of
system’s
trajectory
into
account;
and
(iii)
a
large
class
of
nonlinear
systems
can
be
approximated
by
Takagi-Sugeno
(T-S)
fuzzy
mod-
els
on
any
compact
set
to
arbitrary
accurary
by
using
the
fuzzy
modeling
approach
[39],
the
available
theory
concerning
the
sta-
bility
analysis
and
control
synthesis
of
T-S
fuzzy
systems
is
fairly
mature.
However,
in
the
event-triggerred
framework,
the
prob-
lems
of
stability
and
stabilization
for
event-triggered
networked
T-S
fuzzy
systems
have
received
little
attention.
In
addition,
it
is
worth
mentioning
that
in
some
open
literature,
for
example,
due
to
the
introduction
of
communication
networks
[16,55],
or
time-
varying
sampling
[50,51],
the
time
scales
in
the
premise
variables
of
T-S
fuzzy
models
and
control
are
essentially
different,
which
results
in
the
different
time
scales
in
premise
variables
of
the
global
closed-loop
fuzzy
systems.
However,
this
property
is
ignored
in
the
proof
of
the
main
results
in
[16,55].
Just
as
pointed
out
in
[20,26],
the
results
in
[55]
and
[16]
are
questionable
(Detailed
discussions
can
be
found
in
[20,26]).
Unfortunately,
in
[20,26],
the
authors
did
not
provide
a
feasible
solution
for
solving
such
a
problem.
In
view
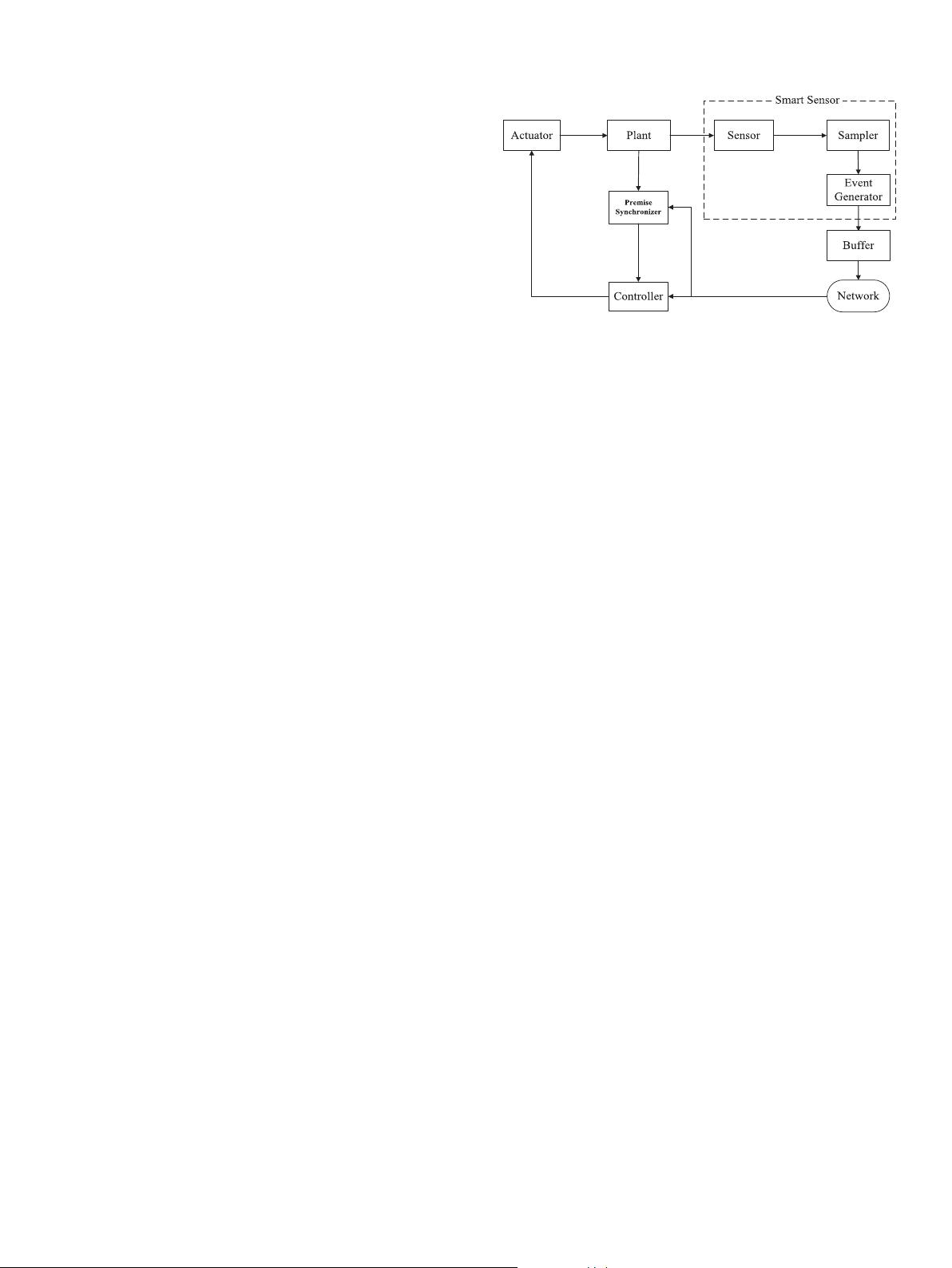
Fig.
1.
Schematic
diagram
of
networked
control
systems
with
event-triggered
com-
munication
scheme.
of
this,
an
interesting
question
is
how
to
deal
with
this
problem
effectively?
Motivated
by
the
above
mentioned
results,
in
this
article,
we
focus
our
attention
on
the
state-feedback
stabilization
problem
of
discrete-time
nonlinear
NCSs
with
ETS
in
the
presence
of
com-
munication
delays
in
T-S
fuzzy
model.
The
main
contributions
of
this
article
are
summarized
as
follows:
(1)
a
more
general
mixed
ETS
for
practical
stability
is
proposed
to
reduce
the
network
band-
width
utilization.
The
key
idea
of
the
proposed
ETS
is
that
if
the
current
sensor
measurement
signal
and
the
previously
transmit-
ted
one
satisfy
a
certain
state-dependent
relation,
then
an
event
is
happening
and
so
to
trigger
event
generator
(shown
in
Fig.
1)
to
transmit
the
sensor
data,
otherwise
no
event
occurs.
Considering
the
effects
of
communication
delays
and
the
proposed
ETS,
com-
bined
with
T-S
fuzzy
model
approach,
an
event-based
discrete-time
T-S
fuzzy
system
model
is
established;
(2)
conditions
for
uniform
utimately
bounded
stability
are
derived
in
the
event-triggered
state
feedback
fuzzy
control
framework.
In
particular,
the
obtained
con-
ditions
characterize
the
relationship
among
the
boundedness
of
the
stability
region,
the
lower
and
upper
bounds
of
the
communication
delays,
triggering
parameters
and
feedback
gains.
Moreover,
as
a
special
case,
a
relative
ETS
for
asymptotic
stability
is
also
proposed.
Under
the
paradigm
of
the
proposed
ETS,
criteria
for
designing
the
event-triggered
fuzzy
controller
are
established
in
terms
of
the
feasibility
of
blinear
matrix
inequalities
(BMIs).
A
co-design
algo-
rithm
is
developed
to
solve
the
BMIs,
and
the
fuzzy
controller
and
triggering
parameters
are
obtained
while
guaranteeing
the
desired
control
performance
and
reducing
the
communication
resource
utilization
simutaneously;
and
(3)
a
premise
synchronizer
has
been
delicately
constructed
to
ensure
the
same
premises
with
uniform
time
scales
in
both
the
T-S
fuzzy
models
and
the
fuzzy
rules
of
par-
allel
distributed
compensation
(PDC)
controller,
which
effectively
overcomes
the
above-mentioned
drawbacks.
Finally,
a
practical
example
is
used
to
illustrate
the
applicability
and
effectiveness
of
the
proposed
method.
Notation:
The
notation
used
throughout
the
article
is
standard.
The
superscripts
“T”
and
“-1”
stand
for
matrix
transposition
and
matrix
inverse,
respectively,
R
n
denotes
the
n−dimensional
Euclidean
space,
Z
+
denotes
the
set
of
positive
integers,
and
the
notation
P
>
0
(≥
0)
means
that
P
is
real
symmetric
and
positive
def-
inite
(semi-definite).
The
symmetric
term
in
a
symmetric
matrix
is
denoted
by
*,
for
example,
X
∗
Y
Z
=
X
Y
T
Y
Z
.
For
any
A
∈
R
n×n
,
we
define
He
(
A
)
=
A
+
A
T
.
I
is
the
identity
matrix
of
appro-
priate
dimensions
and
||
·
||
stands
for
the
Euclidean
vector
norm
or
the
induced
matrix
2-norm
as
appropriate.
A
closed
ball
B
x
=
x
|
x
(
k
)
≤
which
is
centered
at
the
origin
and
with
radius
剩余11页未读,继续阅读
资源评论

weixin_38708361
- 粉丝: 2
- 资源: 918
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功