没有合适的资源?快使用搜索试试~ 我知道了~
资源推荐
资源详情
资源评论

2018025-1
研究与开发
基于 GFFT 的 LFSR 序列生成多项式估计方法
沈利华
(浙江工业大学之江学院,浙江 绍兴 312030)
摘 要:针对线性反馈移位寄存器(LFSR)序列生成多项式的估计问题,提出了一种基于 LFSR 序列有限域
傅里叶变换(GFFT)的估计方法。首先证明了 LFSR 序列 GFFT 的非零点与 LFSR 序列生成多项式的零点之
间的对应关系,进而利用该性质实现 LFSR 序列生成多项式的快速估计,并给出了算法在误码环境下的改进
方法。仿真实验验证了算法的有效性,并对算法的计算复杂度进行了理论分析。和已有算法相比较,本文提
出的算法具有更高的计算效率。
关键词:信号处理;线性反馈移位寄存器;有限域傅里叶变换;生成多项式
中图分类号:TN911.22
文献标识码:A
doi: 10.11959/j.issn.1000−0801.2018025
Generator polynomial estimation of
LFSR sequence based on GFFT
SHEN Lihua
Zhijiang College of Zhejiang University of Technology, Shaoxing 312030, China
Abstract: The problem addressed here is generator polynomial estimation of linear feedback shift register (LFSR)
sequence. An algorithm based on the Galois field Fourier transform (GFFT) was proposed. The relationship between
non-zero points in GFFT of LFSR sequence and zero points in generator polynomial of LFSR sequence was illustrat-
ed firstly. Then the generator polynomial of LFSR sequence was fast estimated based on that property, and the im-
proved method in noisy environment was proposed at last. Validity of the algorithm is verified by the simulation re-
sults, and the computational load is illustrated. The computational efficiency of the proposed algorithm is higher than
that of the existing algorithms.
Key words: signal processing, linear feedback shift register, Galois field Fourier transform, generator polynomial
1 引言
线性反馈移位寄存器(linear feedback shift
register,LFSR)序列因其构造方便,理论成熟,
且具有良好的伪随机和自相关特性,在扩频通信、
通信加扰/加密、航天测控等领域得到了广泛的应
用
[1]
。目前,扩频通信中采用的扩频序列基本上都
是基于 LFSR 生成的,如 m 序列、Gold 序列等
[1-3]
。
同时,为了避免通信过程中数字同步的失锁,常
对通信数据进行加扰处理以有效提高数据的概率
收稿日期:2017−06−12;修回日期:2017−12−14
·59· 电信科学 2018 年第 2 期
转换密度,数据加扰使用的伪随机序列同样由
LFSR 生成
[4]
。对于 LFSR 序列,其生成多项式是
一个非常重要的参数,生成多项式和初始状态可
以唯一确定 LFSR 序列,因此在非合作信号处理
领域,完成 LFSR 序列生成多项式和初相的估计
是对扩频信号进行相关干扰的基础,也是实现数
据解扰、解密的关键。
LFSR 序列生成多项式的估计问题已有较多
研究成果
[5-21]
,最直接的方法主要有组合枚举的
方法
[5]
与基于匹配搜索的方法
[6]
两类,根据 LFSR
输入与输出的关系,列出齐次线性方程组,通
过搜索多项式系数,找出方程组符合最多的解,
即生成多项式系数。该类方法思路简单直接,
但枚举组合时需要进行大量的试探并验证,计
算量较大。
参考文献[7]提出了基于 Walsh-Hadamard 变
换的估计算法,将 LFSR 序列排列成二元域上线
性方程组的系数矩阵,进而利用 Walsh-Hadamard
变换求解其生成多项式,算法要求 LFSR 抽头系
数较少。陈松等人
[8]
利用序列软信息,构建序列
及多项式可信度集合,通过可信度累积实现估计。
参考文献[9]提出了基于高阶统计原理的 m 序列本
原多项式的测定方法。算法寻找含错 m 序列的高
阶统计峰值算得本原多项式的高阶倍式,通过求
解高阶倍式的最大公约式来估计序列的本原多项
式。与基于 Walsh-Hadamard 变换的方法相比,参
考文献[8,9]不再受制于生成多项式的抽头数,但
不足之处在于计算复杂度相对较高。参考文献[10]
提出的算法与之类似,将 LFSR 序列转换为卷积
码
[10]
或分组码
[11,12]
,利用译码的纠错实现 LFSR
序列的生成多项式估计,这两种算法思路较新颖,
但算法过程都比较复杂,步骤繁琐,不易实现。
参考文献[14-17]利用大量数据的统计偏
差,估计生成多项式的倍式,进而利用高阶倍
式的最大公约式得到序列的生成多项式。参考
文献[18-21]同样在信源不平衡的条件下,以游程
距离和相关度等作为信源不平衡性的衡量准则,
通过比特抽取参照的多项式的不平衡性指标,判
定生成的多项式是否正确,该类方法不用事先估
计 LFSR 序列,但主要问题是算法的计算量大,
实时性较差。
从目前的研究成果来看,LFSR 序列生成的
多项式估计着重解决的是算法的容错能力,而
对算法的实时性要求不高。但在现代电子战的
环境下,要求能够实现对通信信号的实时干扰
和信息截获,因此需要研究 LFSR 序列生成多项
式估计的快速方法。对此,本文提出了一种基
于 LFSR 序列有限域傅里叶变换(Galois field
Fourier transform,GFFT)的估计方法,利用
LFSR 序列 GFFT 的频谱中非零点与序列生成多
项式零点的对应关系,实现 LFSR 序列生成多项
式的快速估计。
2 LFSR 序列生成多项式估计的数学模型
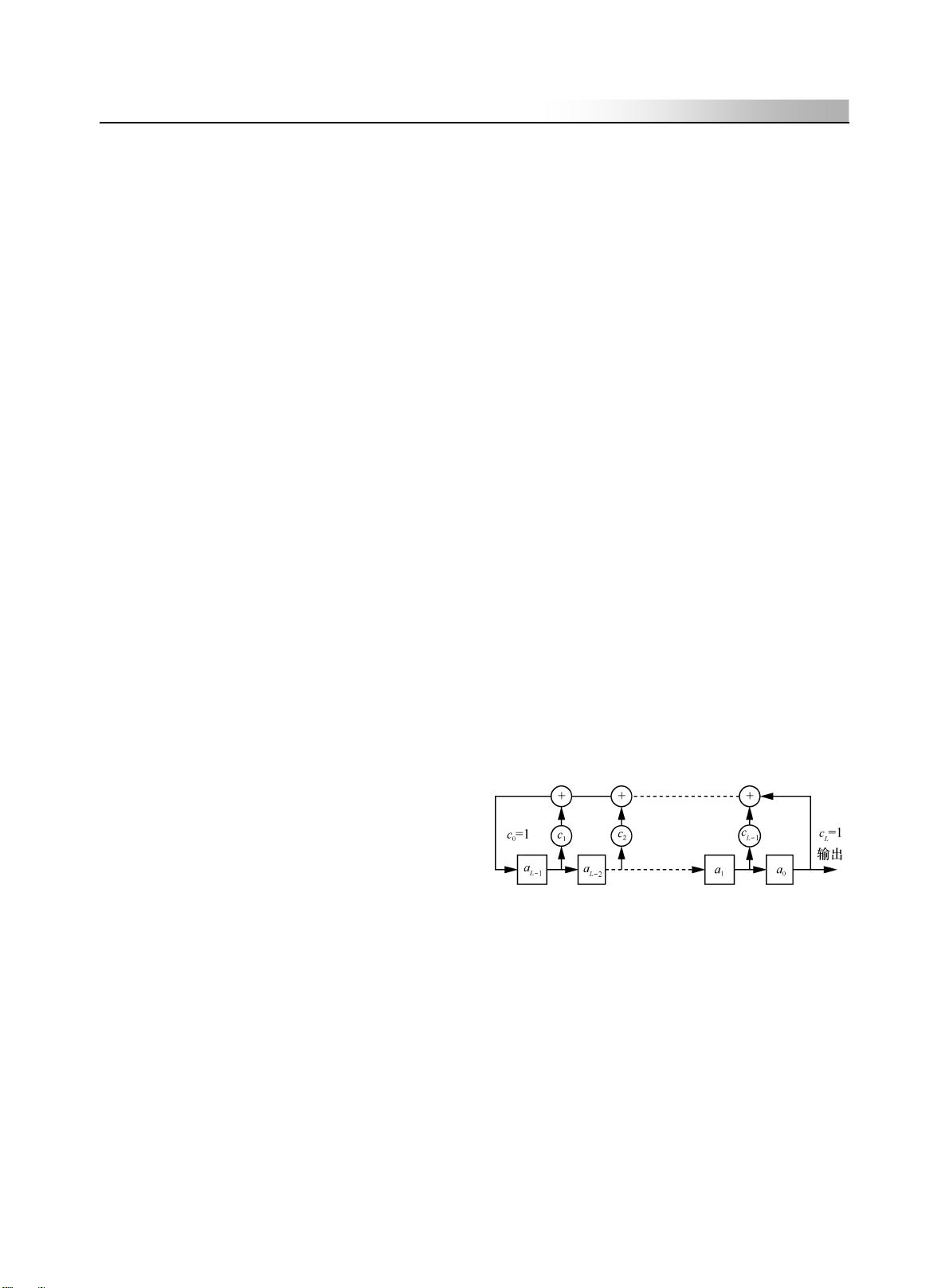
线性反馈移位寄存器的组成如图 1 所示。图 1
中各级移位寄存器的状态分别用
i
a 表示, 0
i
a
=
或
1,i 是整数。反馈线的连接状态用
i
c 表示, 1
i
c
=
表示此线接通(参加反馈), 0
i
c = 表示此线断开。
图 1 线性反馈移位寄存器
设 n 级移位寄存器的初始状态为
12 n
aa a
−− −
"
,
对于任意一状态
k
a
,有:
1
L
kiki
i
aca
−
=
=
∑
(1)
其中,求和按模 2 运算,式(1)为 LFSR 序列递
推方程。
i
c 的取值决定了移位寄存器的反馈连接
和序列的结构,故
i
c 是 LFSR 序列一个很重要的
参量,现将它用式(
2)表示:
2018025-2
剩余6页未读,继续阅读
资源评论

weixin_38704922
- 粉丝: 6
- 资源: 919
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 嵌入式开发_ARM_入门_STM32迁移学习_1741139876.zip
- 嵌入式系统_STM32_自定义Bootloader_教程_1741142157.zip
- 文章上所说的串口助手,工程文件
- 斑马打印机zpl官方指令集
- 《实验二 面向对象编程》
- 《JavaScript项目式实例教程》项目五多窗体注册页面窗口对象.ppt
- Web前端开发中Vue.js组件化的应用详解
- labelme已打包EXE文件
- 一文读懂Redis之单机模式搭建
- Vue综合案例:组件化开发
- 《SolidWorks建模实例教程》第6章工程图及实例详解.ppt
- C语言基础试题.pdf
- Go语言、数据库、缓存与分布式系统核心技术要点及面试问答详解
- 7天精通DeepSeek实操手册.pdf
- DeepSeek R1 Distill 全版本安全评估.pdf
- DeepSeek 零基础入门手册.pdf
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功