没有合适的资源?快使用搜索试试~ 我知道了~
基于校正多相位快速傅里叶变换算法的叠栅条纹相位差测量
2 下载量 188 浏览量
2021-02-12
22:08:52
上传
评论
收藏 5.16MB PDF 举报
温馨提示
叠栅条纹相位差测量是光栅位移测量中的关键技术,在两块光栅相对运动过程中,叠栅条纹信号的频率会因光栅夹角误差的存在而发生偏移,采用传统多相位快速傅里叶变换(MPFFT)算法计算任意时刻叠栅条纹相位值会产生测量误差,导致相位差测量不准确。为了减少频偏所产生的相位测量误差,提出了一种校正MPFFT相位测量算法,推导出了基于相位差校正法的MPFFT谱校正模型。仿真结果表明,在无噪声情况下,当光栅夹角误差为0.1°时,信号的最大频率偏移量约为4.19 kHz,传统MPFFT相位测量误差大于100°,经相位校正后,相位测量误差小于0.2°,相位差测量误差小于0.004°;在高斯噪声和谐波干扰情况下,相位差测量误差小于0.2°,当取栅距为20 μm时,相位差测量误差所产生的位移测量误差小于0.0111 μm,为光栅位移纳米级测量提供了参考。
资源推荐
资源详情
资源评论

书书书
第
34
卷
第
6
期
光
学
学
报
Vol.34
,
No.6
2014
年
6
月
犃犆犜犃犗犘犜犐犆犃犛犐犖犐犆犃
犑狌狀犲
,
2014
基于校正多相位快速傅里叶变换算法的
叠栅条纹相位差测量
常
丽
杨继敏
(沈阳工业大学信息科学与工程学院,辽宁 沈阳
110870
)
摘要
叠栅条纹相位差测量是光栅位移测量中的关键技 术,在 两 块 光 栅 相 对 运 动 过 程 中,叠 栅 条 纹 信 号 的 频 率 会
因光栅夹角误差的存在而发生偏移,采用传统 多 相 位 快 速 傅 里 叶 变 换(
MPFFT
)算法 计 算 任 意 时 刻 叠 栅 条 纹 相 位
值会产生测量误差,导致相位差测量不 准 确。 为 了 减 少 频 偏 所 产 生 的 相 位 测 量 误 差,提 出 了 一 种 校 正
MPFFT
相
位测量算法,推导出了基于相位差校正法的
MPFFT
谱校正模型。仿 真 结 果 表 明,在无 噪 声 情 况 下,当光 栅 夹 角 误
差为
0.1°
时,信号的最大 频率偏 移量约 为
4.19kHz
,传 统
MPFFT
相位 测量误 差大于
100°
,经 相位校 正后,相位测
量误差小于
0.2°
,相位差测量误差小于
0.004°
;在高斯噪声 和 谐 波 干 扰 情 况 下,相 位 差 测 量 误 差 小 于
0.2°
,当取 栅
距为
20
μ
m
时,相位差测量误差所产生的位移测量误差小于
0.0111
μ
m
,为光栅位移纳米级测量提供了参考。
关键词
光栅;叠栅条纹;相位差测量;相位差校正
中图分类号
TH741
文献标识码
A
犱狅犻
:
10.3788
/
犃犗犛201434.0612006
犕狅犻狉犲犉狉犻狀
犵
犲犘犺犪狊犲犇犻犳犳犲狉犲狀犮犲犕犲犪狊狌狉犲犿犲狀狋犅犪狊犲犱狅狀犆狅狉狉犲犮狋犻狀
犵
犕犘犉犉犜 犃犾
犵
狅狉犻狋犺犿
犆犺犪狀
犵
犔犻
犢犪狀
犵
犑犻犿犻狀
(
犛犮犺狅狅犾狅
犳
犐狀
犳
狅狉犿犪狋犻狅狀犛犮犻犲狀犮犲犪狀犱犈狀
犵
犻狀犲犲狉犻狀
犵
,
犛犺犲狀
狔
犪狀
犵
犝狀犻狏犲狉狊犻狋
狔
狅
犳
犜犲犮犺狀狅犾狅
犵狔
,
犛犺犲狀
狔
犪狀
犵
,
犔犻犪狅狀犻狀
犵
110870
,
犆犺犻狀犪
)
犃犫狊狋狉犪犮狋
犕狅犻狉犲犳狉犻狀
犵
犲
狆
犺犪狊犲犱犻犳犳犲狉犲狀犮犲犿犲犪狊狌狉犲犿犲狀狋犻狊狋犺犲犽犲
狔
狋犲犮犺狀狅犾狅
犵狔
狅犳
犵
狉犪狋犻狀
犵
犱犻狊
狆
犾犪犮犲犿犲狀狋犿犲犪狊狌狉犲犿犲狀狋
,
狑犺犲狀狋犺犲狋狑狅
犵
狉犪狋犻狀
犵
狊犪狉犲犻狀狉犲犾犪狋犻狏犲 犿狅狏犲犿犲狀狋
,
犿狅犻狉犲犳狉犻狀
犵
犲狊犻
犵
狀犪犾犳狉犲
狇
狌犲狀犮
狔
犻狊狅犳犳狊犲狋犫犲犮犪狌狊犲狋犺犲狉犲犻狊犪狀犪狀
犵
犾犲
犲狉狉狅狉犫犲狋狑犲犲狀狋犺犲狋狑狅
犵
狉犪狋犻狀
犵
狊
,
狋狉犪犱犻狋犻狅狀犪犾 犿狌犾狋犻
狆
犺犪狊犲犳犪狊狋 犉狅狌狉犻犲狉狋狉犪狀狊犳狅狉犿
(
犕犘犉犉犜
)
犪犾
犵
狅狉犻狋犺犿 犻狊狌狊犲犱狋狅
犮犪犾犮狌犾犪狋犲犿狅犻狉犲犳狉犻狀
犵
犲
狆
犺犪狊犲狏犪犾狌犲犪狋犪狀
狔
狋犻犿犲
,
犻狋狑犻犾犾
狆
狉狅犱狌犮犲 犿犲犪狊狌狉犲犿犲狀狋犲狉狉狅狉狊
,
狉犲狊狌犾狋犻狀
犵
犻狀
狆
犺犪狊犲犱犻犳犳犲狉犲狀犮犲
犿犲犪狊狌狉犲犿犲狀狋犻狊 狀狅狋犪犮犮狌狉犪狋犲.犜狅 狉犲犱狌犮犲 狋犺犲
狆
犺犪狊犲 犿犲犪狊狌狉犲犿犲狀狋犲狉狉狅狉 犮犪狌狊犲犱 犫
狔
犳狉犲
狇
狌犲狀犮
狔
狅犳犳狊犲狋
,
犪
狆
犺犪狊犲
犿犲犪狊狌狉犲犿犲狀狋犪犾
犵
狅狉犻狋犺犿狅犳犮狅狉狉犲犮狋犻狀
犵
犕犘犉犉犜犻狊
狆
狉狅
狆
狅狊犲犱
,
犪狀犱
狆
犺犪狊犲犮狅狉狉犲犮狋犻狅狀犿狅犱犲犾狅犳犕犘犉犉犜狊
狆
犲犮狋狉狌犿犫犪狊犲犱狅狀
狆
犺犪狊犲犱犻犳犳犲狉犲狀犮犲犮狅狉狉犲犮狋犻狅狀犿犲狋犺狅犱犻狊犱犲犱狌犮犲犱.犛犻犿狌犾犪狋犻狅狀狉犲狊狌犾狋狊狊犺狅狑狋犺犪狋犻狀狋犺犲犪犫狊犲狀犮犲狅犳狀狅犻狊犲
,
狑犺犲狀狋犺犲犪狀
犵
犾犲
犲狉狉狅狉犻狊0.1°
,
犿狅犻狉犲犳狉犻狀
犵
犲犿犪狓犻犿狌犿狊犻
犵
狀犪犾犳狉犲
狇
狌犲狀犮
狔
狅犳犳狊犲狋犻狊4.19犽犎狕
,
狋犺犲
狆
犺犪狊犲犿犲犪狊狌狉犲犿犲狀狋犲狉狉狅狉狅犳狋狉犪犱犻狋犻狅狀犪犾
犕犘犉犉犜犻狊犿狅狉犲狋犺犪狀
100°
,
狆
犺犪狊犲犿犲犪狊狌狉犲犿犲狀狋犲狉狉狅狉犻狊犾犲狊狊狋犺犪狀0.2°犪狀犱狋犺犲
狆
犺犪狊犲犱犻犳犳犲狉犲狀犮犲犿犲犪狊狌狉犲犿犲狀狋犲狉狉狅狉犻狊
犾犲狊狊狋犺犪狀0.004°犪犳狋犲狉犮狅狉狉犲犮狋犻狅狀犻狀狋犺犲
狆
狉犲狊犲狀犮犲狅犳犌犪狌狊狊犻犪狀狀狅犻狊犲犪狀犱犺犪狉犿狅狀犻犮狊
,
狋犺犲
狆
犺犪狊犲犱犻犳犳犲狉犲狀犮犲犿犲犪狊狌狉犲犿犲狀狋
犲狉狉狅狉犻狊犾犲狊狊狋犺犪狀0.2°.犠犺犲狀狋犺犲
狆
犻狋犮犺犻狊20
μ
犿
,
狋犺犲犮狅狉狉犲狊
狆
狅狀犱犻狀
犵犵
狉犪狋犻狀
犵
犱犻狊
狆
犾犪犮犲犿犲狀狋犿犲犪狊狌狉犲犿犲狀狋犲狉狉狅狉犻狊犾犲狊狊
狋犺犪狀0.0111
μ
犿
,
犻狋
狆
狉狅狏犻犱犲狊犪狉犲犳犲狉犲狀犮犲犳狅狉狋犺犲
犵
狉犪狋犻狀
犵
狀犪狀狅狊犮犪犾犲犱犻狊
狆
犾犪犮犲犿犲狀狋犿犲犪狊狌狉犲犿犲狀狋.
犓犲
狔
狑狅狉犱狊
犵
狉犪狋犻狀
犵
狊
;
犿狅犻狉犲犳狉犻狀
犵
犲
;
狆
犺犪狊犲犱犻犳犳犲狉犲狀犮犲犿犲犪狊狌狉犲犿犲狀狋
;
狆
犺犪狊犲犱犻犳犳犲狉犲狀犮犲犮狅狉狉犲犮狋犻狅狀
犗犆犐犛犮狅犱犲狊
120.5050
;
120.4120
;
050.2770
收稿日期:
20131111
;收到修改稿日期:
20140129
基金项目:沈阳市科技计划项目(
F13316157
)
作者简介:常
丽(
1971
—),女,博士,副教授,主要从事精密测量与控制,智能仪器与网络化测控系统等方面的研究。
Email
:
chan
g
lianli
@
163.com
1
引
言
光栅位移测量技术是以叠栅条纹细分理论为基
础,通常采用测量条纹的相位变化量获得位移量,高
精度测量相位是提高光栅位移测量分辨率和精度的
基础
[
1-3
]
。目 前,常 采 用
CCD
/
CMOS
图 像 传 感 器
作为叠栅条纹接收 器 件
,其 分 辨力 主 要受 像 素尺 寸
06120061
光
学
学
报
限制,像素尺寸越小,一个条纹周期内所包含的像素
数越 多,位 移 测 量 分 辨 力 就 越 高。 基 于
CCD
/
CMOS
传感器 输 出 的 叠 栅 条 纹 信 号 具 有 较 好 的 周
期性,通过求取相邻两次叠栅条纹相位差可以获得光
栅相对位移量,光栅相对位移量
Δ
狓
与叠栅条纹相位
差
Δ
φ
、栅距
犱
之间的关系为
Δ
狓
=
犱
×
Δ
φ
/
360°
,因此,
提高位移测量精度的关键是提高相位差的测量精度。
传统的基 于傅里 叶变换 的相位 测量方 法,由 于
加窗 截 断 产 生 的 频 谱 泄 漏 严 重 影 响 相 位 测 量 精
度
[
4-5
]
。多相位快 速 傅 里 叶 变 换 (
MPFFT
)等 算 法
能够减少这类误差,与传统的傅里叶变换相比,一定
程度上抑制了频谱泄漏。但上述两种算法的测相精
度均受到信号频偏的影响,当两块光栅相对运动时,
不可避免地会产生 光 栅夹 角 误差,造 成 叠栅 条 纹信
号频率的偏移,产生相位测量误差,且不同频偏下所
产生的相位测量误 差 也不 同,导致 相 位差 测 量结 果
不准确
[
6-7
]
。基于以上原 因,本文 在
CMOS
采集 叠
栅条纹信号的 基 础上,提 出了 一 种 校 正
MPFFT
相
位测量算法,减少了因 光 栅相 对 运动 引 起的 频 偏对
相位测量的影响,提高相位差测量精度。
2
叠栅条纹数学模型
把两块光 栅以微 小夹角 叠放在 一起,当有平行
光照射时,在光栅背后就会出现明暗相间的条纹,即
叠栅条纹。
叠栅条纹在
狓
方 向 上 的 光 强 表 达 式 可 近 似 表
示为
犐
(
狓
)
=
犐
0
+
犐
cos
(
2
π
犳
狓
狓
+
φ
), (
1
)
式中
犐
0
为背景光强,
犐
为叠栅条纹光强变化幅度,
犳
狓
为叠栅条纹在
狓
方向上的空间频率,
犳
狓
=
1
/
犠
,
φ
为
光学初相位,
犠
为叠栅条纹周期。
在驱动脉冲作用下,
CMOS
图像 传 感器 开 始对
叠栅条纹 信号进 行采集
[
8
]
,将静 态叠栅 条纹光 强信
号转换成随时间变化 的 近似 正 弦波 的 动态 电 信号。
光电转换后的电信号可表示为
狔
(
狋
)
=
犝
0
+
犝
1
cos
(
2
π
犳
狓
犔犉狋
+
φ
), (
2
)
式中
犝
0
为电信号的直流分量,
犝
1
为电信号的幅度,
犔
为传感器有效光敏元长度,
犔
=
犿
×
犖
,
犿
为传感
器的 像 素 尺 寸,
犖
为 有 效 像 素 数,
犉
为 帧 频,
犉
=
犳
s
/
犖
,
犳
s
为采样频率。
由于
CMOS
传感器为像素阵列结构,且内部集
成像素级模数(
A
/
D
)转换 器,其输 出 的叠 栅 条纹 信
号就是被像素抽样 了 的信 号,并且 具 有很 好 的周 期
性。
CMOS
输出叠栅条纹信号表达式为
狔
(
狀
)
=
犝
0
+
犝
1
cos
(
2
π
狀
犳
狓
犔犉
/
犳
s
+
φ
)
.
(
3
)
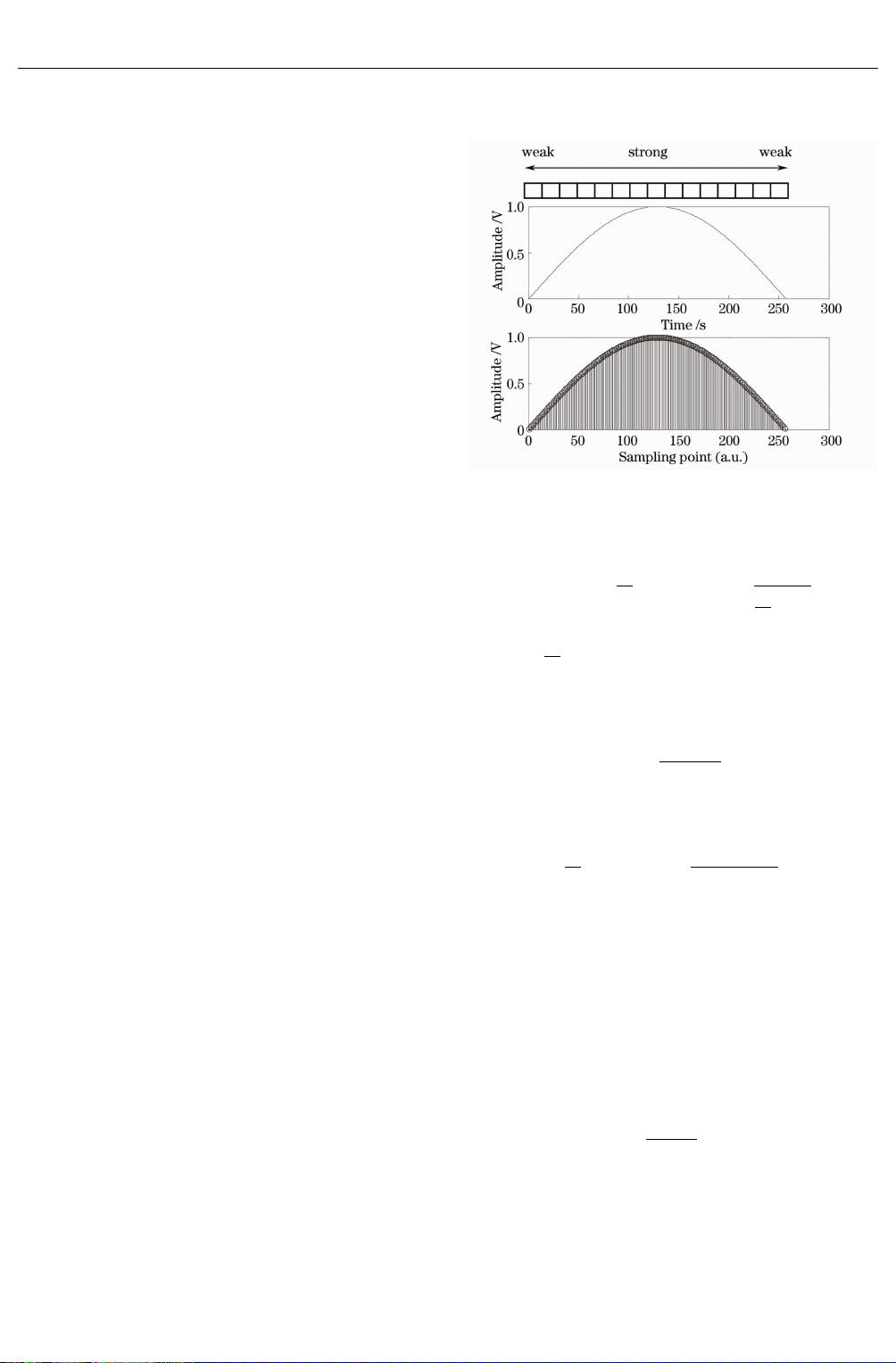
叠栅条纹采集过程如图
1
所示。
图
1
叠栅条纹采集过程
Fi
g
.1 Procedureofmoirefrin
g
eac
q
uisition
由(
2
)式可知,令叠栅条纹信号频率为
犳
,则
犳
=
犳
狓
犔犉
=
1
犠
×
(
犿
×
犖
)
×
1
1
犳
s
×
犖
=
1
犠
×
犿
×
犳
s
.
(
4
)
根 据 叠 栅 条 纹 周 期
犠
与 光 栅 夹 角
θ
[单 位:
(
°
)]、栅距
犱
的关系:
犠
=
犱
×
180
θ
×π
, (
5
)
将(
5
)式代入(
4
)式,可以 得到光 栅 夹角 与 叠栅 条 纹
信号频率的关系为
犳
=
1
犠
×
犿
×
犳
s
=
犿
×
犳
s
×
π
犱
×
180
×
θ
.
(
6
)
由(
6
)式可知,叠栅条纹信号的频率会因光栅相
对运 动 所 产 生 的 夹 角 误 差 而 发 生 偏 移。 采 用 的
CMOS
传感器的像素尺寸为
4
μ
m
、最高采样频率为
12MHz
,采用栅距为
20
μ
m
的光栅。采用
512
点快
速傅里叶变换(
FFT
)计算,因 此 调整 两 光栅 夹 角为
0.56°
,此时叠栅条纹周期
犠
约为
2048
μ
m
,叠栅 条
纹信号的频率
犳
约为
23.44kHz
。由(
6
)式进 一 步
可得到夹角误差
Δ
θ
与频率误差
Δ
犳
的关系:
Δ
犳
=
40
×
π
3
×Δ
θ
.
(
7
)
图
2
为夹角误差与频率误差的关系曲线。
根据图
2
可知,当夹角误差为
±0.1°
时,所产生
的最大频率 误 差 为
±4.19kHz
,采 用 传 统
FFT
和
MPFFT
均会产生 相 位 测 量 误 差,且 不 同 频 偏 下 所
产生的相位测量误 差 也不 同,导致 相 位差 测 量结 果
06120062
剩余6页未读,继续阅读
资源评论

weixin_38704386
- 粉丝: 3
- 资源: 917
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功