python实现各种插值法实现各种插值法(数值分析数值分析)
一维插值一维插值
插值不同于拟合。插值函数经过样本点，拟合函数一般基于最小二乘法尽量靠近所有样本点穿过。常见插值方法有拉格朗日插值法、分段插值法、样条插值法拉格朗日插值法、分段插值法、样条插值法。
拉格朗日插值多项式：当节点数n较大时，拉格朗日插值多项式的次数较高，可能出现不一致的收敛情况，而且计算复杂。随着样点增加，高次插值会带来误差的震动现象称为龙格
现象。
分段插值：虽然收敛，但光滑性较差。
样条插值:样条插值是使用一种名为样条的特殊分段多项式进行插值的形式。由于样条插值可以使用低阶多项式样条实现较小的插值误差，这样就避免了使用高阶多项式所出现的龙格
现象，所以样条插值得到了流行。
# -*-coding:utf-8 -*-
import numpy as np
from scipy import interpolate
import pylab as pl
x=np.linspace(0,10,11)
#x=[ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.] y=np.sin(x)
xnew=np.linspace(0,10,101)
pl.plot(x,y,"ro")
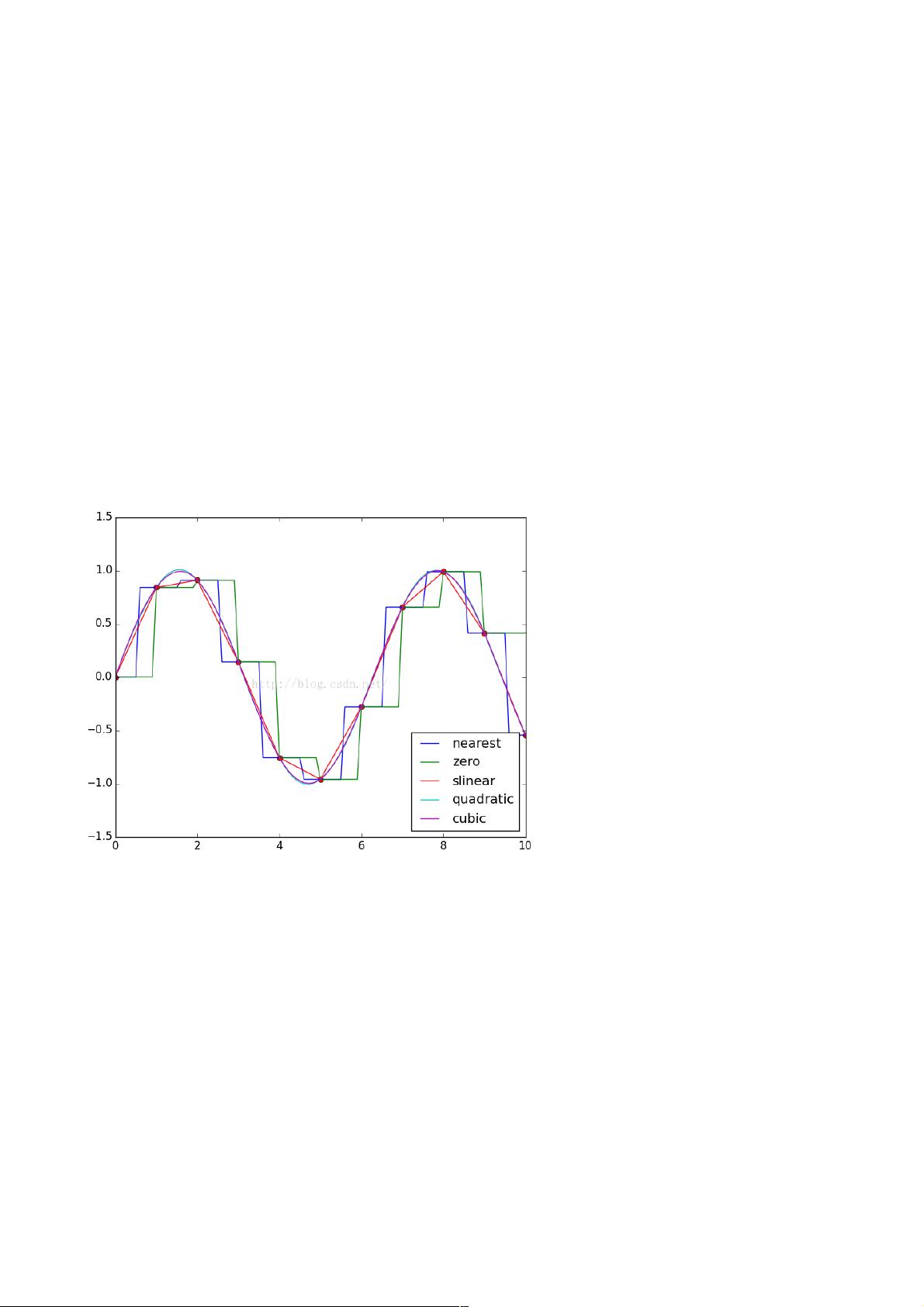
for kind in ["nearest","zero","slinear","quadratic","cubic"]:#插值方式
#"nearest","zero"为阶梯插值
#slinear 线性插值
#"quadratic","cubic" 为2阶、3阶B样条曲线插值
f=interpolate.interp1d(x,y,kind=kind)
# ‘slinear', ‘quadratic' and ‘cubic' refer to a spline interpolation of first, second or third order)
ynew=f(xnew)
pl.plot(xnew,ynew,label=str(kind))
pl.legend(loc="lower right")
pl.show()
结果：
二维插值二维插值
方法与一维数据插值类似，为二维样条插值。
# -*- coding: utf-8 -*-
"""
演示二维插值。
"""
import numpy as np
from scipy import interpolate
import pylab as pl
import matplotlib as mpl
def func(x, y):
return (x+y)*np.exp(-5.0*(x**2 + y**2))
# X-Y轴分为15*15的网格
y,x= np.mgrid[-1:1:15j, -1:1:15j]
fvals = func(x,y) # 计算每个网格点上的函数值 15*15的值
print len(fvals[0])
#三次样条二维插值
newfunc = interpolate.interp2d(x, y, fvals, kind='cubic')
# 计算100*100的网格上的插值
xnew = np.linspace(-1,1,100)#x
ynew = np.linspace(-1,1,100)#y
fnew = newfunc(xnew, ynew)#仅仅是y值 100*100的值
# 绘图
# 为了更明显地比较插值前后的区别，使用关键字参数interpolation='nearest'
资源评论
weixin_38694299
- 粉丝: 5
- 资源: 948
