[小白系列]sigmoid和tanh激活函数的绘制(分开画，合起来画，总有一款适合你），逐行代码详解

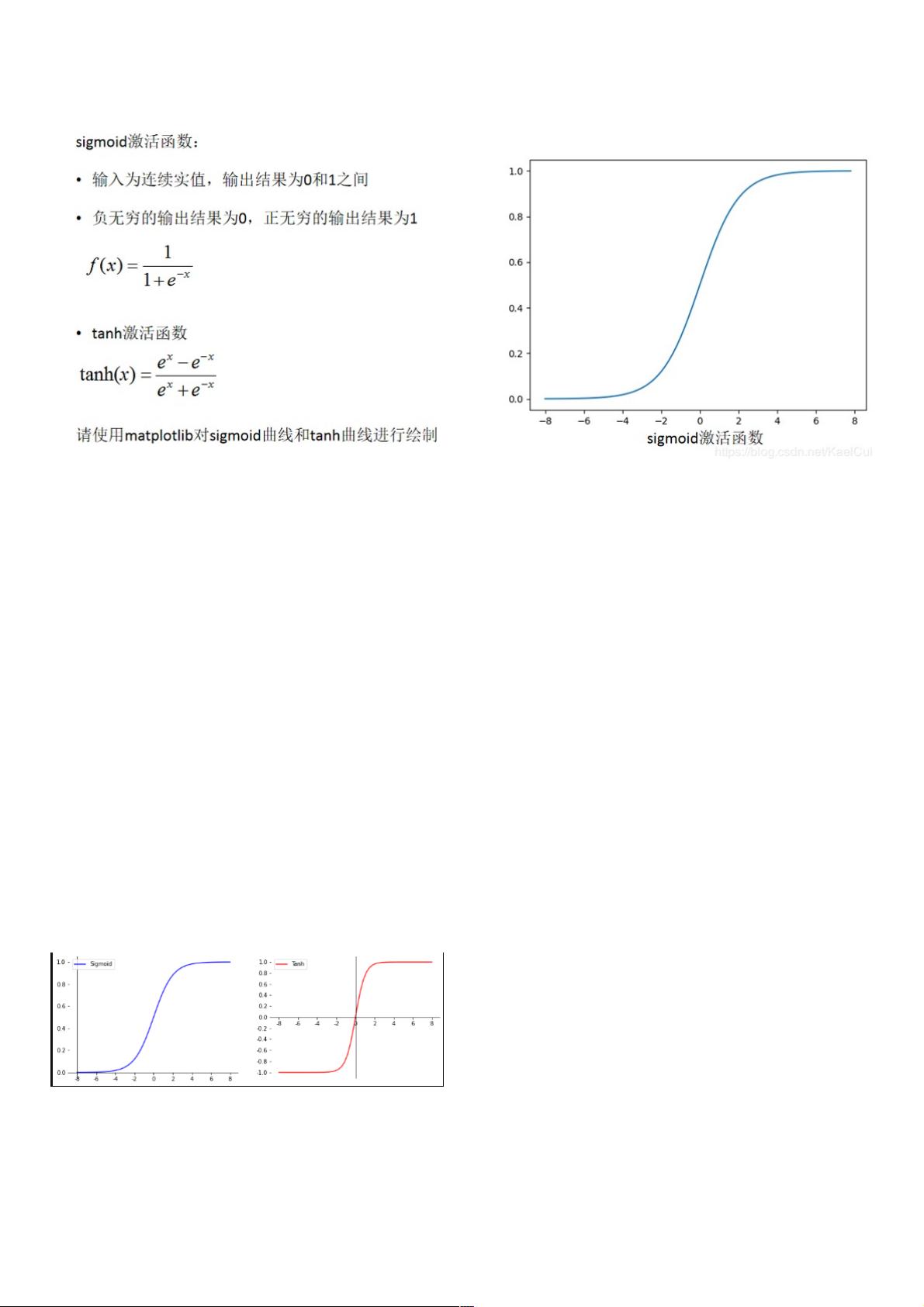
第一种：分开来画 import matplotlib.pyplot as plt import numpy as np plt.rcParams['axes.unicode_minus'] = False def sigmoid(x): return 1.0/(1.0+np.exp(-x)) def tanh(x): return (np.exp(x) - np.exp(-x))/(np.exp(x)+np.exp(-x)) x = np.linspace(-8,8) fig = plt.figure(figsize = (12,4)) ax1 = plt.subplot(12 在神经网络中，激活函数是不可或缺的组成部分，它们赋予了网络模型非线性特性，使得模型能够处理更复杂的任务。本篇文章将详细讲解两种常见的激活函数——Sigmoid和Tanh，并通过Python代码演示如何分别绘制它们的图形以及如何将它们合在一起画在同一张图上。 Sigmoid函数，也称为Logistic函数，表达式为： \[ f(x) = \frac{1}{1 + e^{-x}} \] 它的输出值域在0到1之间，形似S型曲线，常用于二分类问题，因为它可以将输入映射到概率空间。在代码中，我们定义了一个sigmoid函数，使用numpy库的exp函数计算指数部分，然后进行求解： ```python def sigmoid(x): return 1.0 / (1.0 + np.exp(-x)) ``` 接下来，我们使用matplotlib库绘制Sigmoid函数的图像。设置图表大小、轴的显示与位置，以及刻度和标签，最后绘制函数曲线并显示图例： ```python x = np.linspace(-8, 8) fig = plt.figure(figsize=(12, 4)) ax1 = plt.subplot(121) # ... (设置轴的显示、位置、刻度等) plt.plot(x, sigmoid(x), label='Sigmoid', color='blue') plt.legend() ``` Tanh函数，全称双曲正切函数，表达式为： \[ f(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \] 其输出值域在-1到1之间，形状与Sigmoid类似但更对称。同样，我们定义一个tanh函数，然后绘制图形： ```python def tanh(x): return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x)) # ... (绘制Sigmoid后) ax2 = plt.subplot(122) # ... (设置轴的显示、位置、刻度等) plt.plot(x, tanh(x), label='Tanh', color='red') plt.legend() ``` 对于第二种情况，我们将Sigmoid和Tanh函数绘制在同一张图上。这里利用了一个数学推导，因为Tanh函数可以表示为2倍Sigmoid函数减1，即： \[ \tanh(x) = 2 \cdot \sigma(2x) - 1 \] ```python x = np.linspace(-10, 10) y = sigmoid(x) tanh = 2 * sigmoid(2 * x) - 1 # ... (设置图表和轴的属性) plt.plot(x, y, label="Sigmoid", color="blue") plt.plot(2 * x, tanh, label="Tanh", color="red") plt.legend() ``` 通过这种方式，我们可以直观地比较Sigmoid和Tanh函数的形状差异。Sigmoid函数在接近0时梯度较小，可能导致梯度消失问题，而Tanh函数则相对更对称，梯度分布更均匀。 选择激活函数应考虑具体任务的需求，如二分类问题可能更适合Sigmoid，而Tanh在某些情况下能提供更好的性能。理解这些函数的性质及其在神经网络中的作用是深度学习初学者的基础知识。更多复杂内容可参考作者GRIT_Kael的其他文章进行深入学习。