过渡金属原子单边缘终止的之字形a-石墨烯纳米带的半金属性和自旋极化输运性质资源-CSDN文库

133 浏览量 2021-03-13 18:25:26 上传评论收藏 2.78MB PDF 举报

本篇研究论文的标题为《过渡金属原子单边缘终止的之字形a-石墨烯纳米带的半金属性和自旋极化输运性质》，旨在探讨通过过渡金属原子对之字形a-石墨烯纳米带单边缘终止后所产生的半金属性和自旋极化输运性质。文章中，研究者利用非平衡格林函数方法和自旋极化密度泛函理论对具有3d过渡金属原子钝化的之字形a-石墨烯纳米带的电子输运性质进行了研究。研究结果表明，Fe、Co和Ni掺杂在纳米带边缘时会表现出半金属性。文章中所提到的3d过渡金属边缘导致之字形a-石墨烯纳米带的电流产生较大的自旋极化。此外，研究还观察到了一些有趣的现象，如半金属性、自旋极化效应和负微分电阻行为。在研究背景中提到，二维(2D)纳米材料由于其独特的电子性质和广泛的应用前景而受到广泛关注。通过吸附过渡金属(TM)来操控二维单层材料如石墨烯的物理性质是实现实际应用的一个重要挑战。研究中指出的石墨烯类似材料a-石墨烯，是一种具有新颖电子结构的二维碳同素异形体。自旋极化密度泛函理论是一种理论工具，用以分析和计算材料体系的电子结构，特别是自旋极化效应。在自旋电子学器件设计中，通过引入磁性材料或通过外部磁场控制电子的自旋取向，是实现电子输运性质调控的重要手段。本研究通过理论计算，指出了对之字形a-石墨烯纳米带的边进行特定金属原子终止是实现半金属性和高自旋极化输运的有效途径。文章中提到的之字形a-石墨烯纳米带具有特定的结构特征，其具有线性色散关系的狄拉克点，以及可以形成一维导电通道的边缘态。当掺杂特定的过渡金属原子时，这些边缘态会发生变化，从而导致材料的电子性质发生改变。特别是3d过渡金属原子的引入，能够改变电子的能量分布，为实现半金属性和自旋极化提供了可能。研究中提到的非平衡格林函数方法是一种理论模拟手段，可以用来研究有限温度下的电子输运特性，尤其是在非平衡状态下的输运行为。通过这种计算方法，研究者能够探究材料在不同电压、温度或外部磁场作用下的电子输运现象，包括电流-电压(I-V)特性曲线以及自旋相关的输运特性。负微分电阻(NDR)是电子器件中的一种特殊现象，指的是在一定的电压范围内，随着施加电压的增加，电流反而减少的现象。NDR在自旋电子器件中具有潜在的应用，例如在存储器、逻辑器件和振荡器中。研究发现，掺杂过渡金属原子后的之字形a-石墨烯纳米带中能够观察到NDR效应，这意味着掺杂后的纳米带在特定条件下能够作为有源区来实现电流调控。在实际应用层面，这篇文章的研究结果为基于之字形a-石墨烯纳米带的自旋电子学器件的自旋极化电子输运性质调控提供了一种新的思路。通过对纳米带边缘的精确修饰，可以实现对器件电流中自旋极化状态的操控，这在未来的自旋电子学和量子计算等领域具有重要的应用前景。通过自旋极化输运性质的操控，有望实现更高效率和更快响应时间的自旋电子器件。本研究论文详细探讨了过渡金属原子单边缘终止的之字形a-石墨烯纳米带在半金属性和自旋极化输运性质方面的理论特性。通过特定的理论计算方法，揭示了该材料系统中电子输运的内在机制，并讨论了其在自旋电子学器件中的潜在应用价值。这些发现为未来相关领域的研究和器件开发提供了重要的理论依据和指导。

资源推荐

资源详情

资源评论

Half-metallicity and spin-polarization transport properties in

transition-metal atoms single-edge-terminated zigzag

-graphyne

nanoribbons

Mingjun Li

, Dan Zhang

, Yongli Gao

, Can Cao

, Mengqiu Long

School of Material Science and Engineering, Central South University, Changsha 410083, PR China

Institute of Super-microstructure and Ultrafast Process in Advanced Materials, School of Physics and Electronics, Central South University, Changsha

410083, China

Department of Physics and Astronomy, University of Rochester, Rochester, NY 14627, USA

article info

Article history:

Received 27 November 2016

Received in revised form

13 February 2017

Accepted 14 February 2017

Available online 16 February 2017

Keywords:

Zigzag

-graphyne nanoribbons (Z

GyNRs)

3d transition-metal termination

Spin-polarized density functional theory

Half-metal

Spin-polarization

Negative differential resistance

abstract

By employing the non-equilibrium Green's function method a nd the spin-polarized density functional

theory, we investigate d the spin-resolved electronic transport properties of the zigz ag

-graphyne

nanoribbons (Z

GyNRs) pas sivated with 3d transition-metal atoms at one of the ribbon edge. Our

results exhibit half-metallic behavior in response to the Fe- , Co- and Ni-doping at the edge of Z

GyNRs.

The 3d transition-metal edge in troduced in this paper can result in large spin polarization on currents

of the Z

GyNRs devices, and som e interesting phenomena suc h as half-metallicity, spin-polarization

effect and negative differential resistance behavi or can be observed. These theoretical results suggest a

rout e to manipulate the spin-resolved electronic transport properties in Z

GyNRs-based spintronics

devices.

1. Introduction

Two-dimensional (2D) nano-materials have attracted great

attentions due to their unique electronic properties and wide

range of promising technological utilizations [1 e4]. Manipulating

the physical properties of 2D monolayer sheets such as graphene

through adsorbing transition metal (TM) is an important ch al-

lenge for realizing their application i n spintronics and nano-

electronics [5e9]. Graphene exhibits m any remarkable propert ies

[10,11], such as Dirac cone [12], high carrier mobility at room

temperature [13], Quantum spin Hall effect [14], and many other

novel phenomena and e lectronic properties [15]. Graphene has

also been extensively explored for inducing electronic spin po-

larization by chemical functionalization and doping [16e19].

However, the gapless band structure of graphene limits its

application in electron ic devices. Recently, graphyne, a nano ma-

terial isostructural graphene, has ignited substantial interests

owing to their extraordinary electroni c, optical, and structural

properties [20,21].

Although a single sheet of graphyne has still not been available,

it is a highly challenging task now. Nevertheless, in 2010, large

area ﬁlms (~3.6 cm

) of graphdiyne (an allotrope of graphyne)

have b een successfully fabricated on a copper surface by a cross

cou pling reaction using hexaethynylbenzene [22], which is a big

step towards the preparation of graphynes, and encouraging

continuous effort for more extended struc tures. Graphyne is

composed of sp- and sp

-hybri zed ca rbon atoms, which can pro-

vid e an extra ﬂexibility in modulation of its structure. Unlike

graphene , graphyne is a semiconductor with a narrow ban d gap,

which may provide a golden opportunity to use them in electronic

device [23,24]. Graphyne has many allotropes such as

-graphyne,

-graphyne, and graphdiyne [25,26] .Andthetheo-

retical researches have been demonstrated that these graphynes

are assumed to be chemically stable [27]. Malko et al. found that

-graphyne is a new di rac cone material, which electronic p rop-

erties of

-graphyne is quite similar to that of graphene [28,29].

Similar to graphene nanoribbons (GNRs), the

-graphyne can also

be tailored into nanoribbons, and can be mainly classiﬁed into two

* Corresponding author.

E-mail address: mqlong@csu.edu.cn (M. Long).

Contents lists available at ScienceDirect

Organic Electronics

journal homepage: www.elsevier.com/locate/orgel

http://dx.doi.org/10.1016/j.orgel.2017.02.018

Organic Electronics 44 (2017) 168e175

types: zigzag

-graphyne nanoribbons (Z

GyNRs) and armchair

-graphyne nanoribbons (A

GyNRs). All of A

GyNRs are

nonmagnetic, and the band gap oscillates with a period of three

when the ribbon width increases [30], while the Z

GyNRs have a

stable antiferromagnetic conﬁguration [31]. Yue et al. demon-

strated the bipolar spin-ﬁltering effect in the symmetric Z

GyNRs,

and found the 100% spin-polarized current can be produced and

modulated by the direction of bi as voltage and/or magnetization

conﬁguration of the electrodes [32].

To expand its practical applicati on in spintronics, doping

graphyne nanoribbons with 3d transition-metal atoms has been

considered as an effective way [33e35]. He et al. found tha t the

adsorption of 3d tran sition-metal atom not only efﬁciently mod-

ulates the elect ronic structures of graphyne, but also introduces

excellent magnetic properti es [36]. Since previous calculations

have indicated that the edge states have a signiﬁcant effect on the

nanoribbons' electronic and magnetic properties [16] ,inthispa-

per we mainly focus on the effects of 3d transition terminated

atoms doping on the s ingle-edge-passivated Z

GyNRs. From ﬁrst

principal method, the sp in-dependent transport properties of Fe-,

Co- and Ni-passivated Z

GyNRs are calculated, and we suggest a

route to manipulate spin current and design the spintronics

devices.

2. Model and method

The structural optimizations and spin-dependent t ransport

properties are performed by the Atomistix ToolKit (ATK) package

[37,38], which is based on the spin density functional theory (DFT)

and the fully self-cons istent non-equilibrium Green's function

(NEGF) method. The local spin density approximation (LSDA) is

employed for the exchange-correlation potential. The wave

functions of all the atoms are expanded by double-zeta pola rized

basis set. The real space grid technique is used with the en ergy

cutoff of 200 Ry as the required cutoff energy in numerical in-

tegrations. The k-point sampling 1, 1, and 100 are used in t he x, y, z

direction, respectively, where z is the direction of electron trans-

port. A vacuum layer of 16 Å is added in x and y di rections to avoid

the interaction between adja cent ribbons . The electronic states of

the electrodes are obtained from a st andard bulk ca lculation. The

basis set is a dopted for elements of systems and the convergence

criterion for the total energy is 10

5

Ry to achieve a balance be-

tween calcul ation efﬁciency and accuracy. The electron temper-

ature is set to 300 K. The geometrical structures are fully

optimized in the presence of the two-leads until the residual force

on each atom is smaller than 0.01 eV/Å. The spin-polarized cur-

rent through the s ystem is calculated using the Land auer-Büttiker

formula [3 9],

ðV

Þ¼

ðV

ðE; V

Þ½f

ðE; V

Þf

ðE; V

ÞgdE (1)

where e is the electron charge, h is the Planck's constant, and T

the transmission of an electron with spin

. f

LðRÞ

ðE; V

Þ is the

Fermi-Dirac distribution function of the l eft (right) electrode, and

LðRÞ

ðV

Þ is the chemical potential of the left (right) electrode,

which depends on th e exte rnal bias voltage, V

. Under the

external bias V

, the electrochemical potential of the left and right

electrodes will be moved rigidly relative to each other, that

is,

ðV

Þ¼

ð0ÞþeV

=2and

ðV

Þ¼

ð0ÞþeV

=2.T

is obtained

from the equation,

ðE; V

Þ¼Tr

(

ðE; V

)

ðE; V

 Im

(

ðE; V

)

ðE; V

(2)

where G

ðG

Þ is the retarded (advanced) Green's function matrix,

and

Þ is the retarded self-energy matrix for the left (right)

electrode.

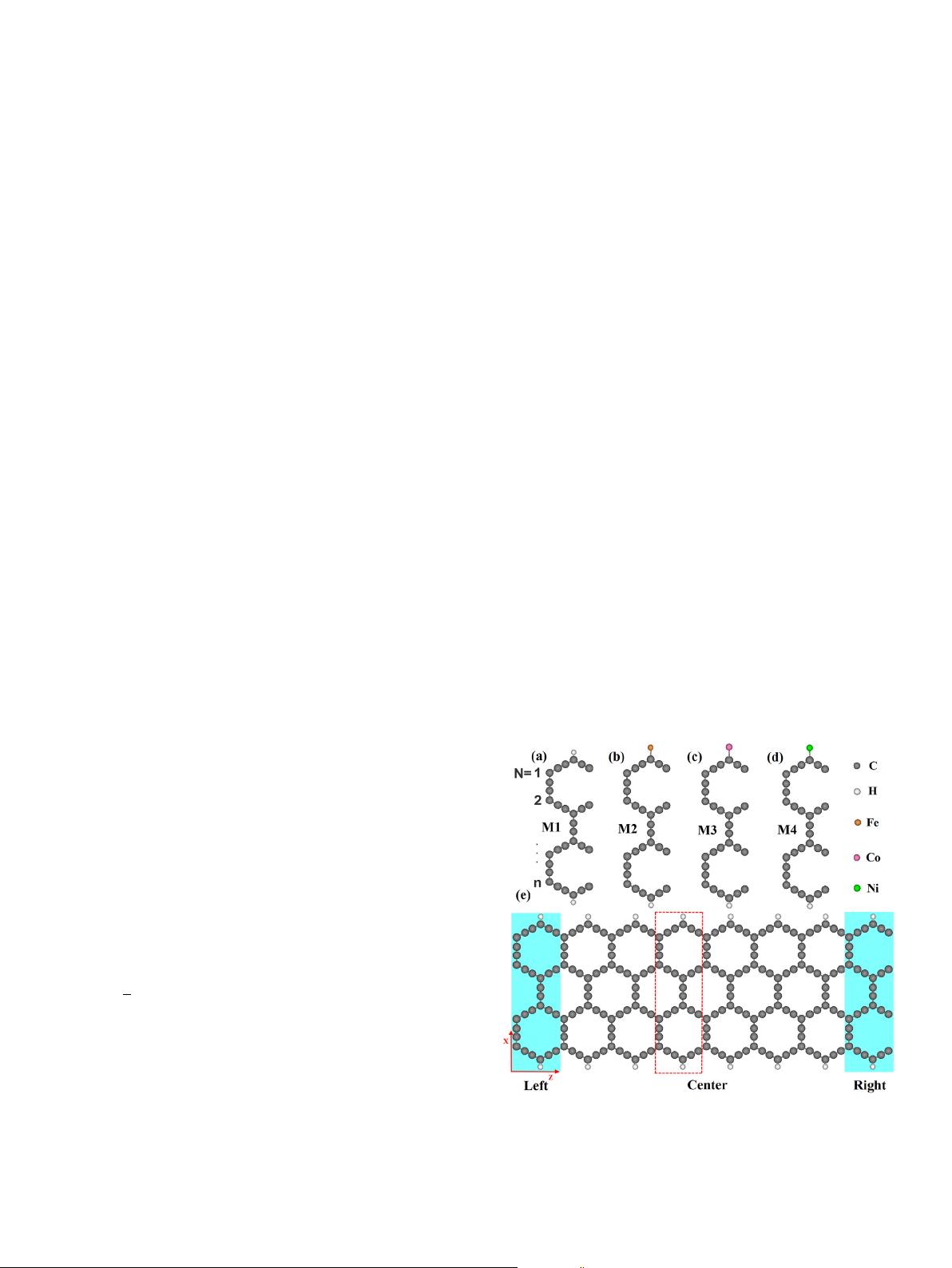
3. Results and discussions

The Z

GNRs are originally obtained by cutting a 2D

-graphyne

along zigzag direction, and the edge carbon atoms are passivated by

single-H atoms to remove the dangling bonds. The studied models

are shown in Fig.1. The blue shade areas are presented the electrode

repeat units. Considering the electronic properties of Z

GyNRs [30]

and the calculated amount, the ribbon widths of 4 (about 2.5 nm)

have been chosen, and both edges are passivated by single-H atoms,

denoted as H-4Z

GyNRs-H, short for M1, as shown in Fig. 1(a). In

order to realize the spin-polarization in H-4Z

GyNRs-H, we also

adopt 3d transition-metal atoms (Fe, Co and Ni) to substitute the H

atoms on one edge as Fe-4Z

GyNRs-H, Co-4Z

GyNRs-H and

Ni-4Z

GyNRs-H as shown in Fig. 1(bed), for convenience, we

labeled them as M2, M3, and M4, respectively. Take M1 for example,

the corresponding device structure is shown in Fig. 1(e), which

consists of three parts: the left electrode, the center scattering re-

gion, and the right electrode. It is noted that the electrodes and the

contact between graphyne and the electrodes have crucial in-

ﬂuences on the spin-polarized electronic transport properties of the

GyNRs. Nevertheless, the contact between graphyne and the

electrodes is very complex in real practices, we thus just only

considered the internal electronic transport properties in Z

GyNRs

and a supercell of Z

GyNRs has been taken as electrode in our

calculations.

Fig. 1. (aed) The structure unit cells of M1-M4, respectively. The numbers denote

different C atoms along one hexagonal side. (e) Two-probe model of M1, and the Left,

Center, and Right represent the lef t electrode, the center scattering region and the right

electrode, respectively. The geometry in red dashed rectangle is unit cell. (For inter-

pretation of the references to colour in this ﬁgure legend, the reader is referred to the

web version of this article.)

M. Li et al. / Organic Electronics 44 (2017) 168e175 169

剩余7页未读，继续阅读

评论收藏

内容反馈

weixin_38691319

粉丝: 3
资源: 908

过渡金属原子单边缘终止的之字形a-石墨烯纳米带的半金属性和自旋极化输运性质

网络技术-网络基础-单层石墨纳米结构中电子自旋输运性质的研究.pdf

网络技术-网络基础-石墨烯基微纳结构中自旋相关的电子输运特性研究.pdf

自旋轨道耦合下铁磁单层石墨烯的自旋输运

氮原子吸附锯齿型石墨烯纳米带第一原理研究

具有不对称边缘氢化作用的n型掺杂之字形石墨烯的边缘接触依赖性自旋输运

铁磁半导体_d波超导结的自旋极化输运.pdf

自旋半导体纳米热电材料器件的高自旋极化电流.pdf

网络技术-网络基础-新型碳基纳米材料的电子结构和输运性质的理论研究.pdf

碳链-之字形石墨烯纳米带纳米结中的自旋滤波和大磁阻行为

单壁碳纳米管超声裂解制备石墨烯纳米带

吸附有V原子或V-苯化合物的曲折边缘石墨烯纳米带的可调谐半金属性能和自旋塞贝克效应

具有对称和不对称边缘氢化作用的锯齿形边缘石墨烯纳米带中的自旋滤镜效应

具有被磷和氢原子钝化的各种边缘结构的石墨烯纳米带的磁电子性质

网络技术-网络基础-单分子磁体的自旋电子输运.pdf

基于扶手椅边缘的石墨烯纳米带的纳米结构的磁结构和磁输运特性

自旋光电流与电流诱导的电子自旋极化——半导体自旋电子学的新进展.pdf

有机半导体的自旋注入和自旋输运.pdf

The electron transport modulated with phonon in graphene nanoribbons

夹在石墨烯纳米带电极之间的三角石墨烯的磁输运性质

连接至V形锯齿形石墨烯纳米带的过渡金属（Cu，Fe）酞菁的电子输运性质

碱金属自旋极化系综的动力学建模与仿真_毕业论文.pdf

在锯齿形石墨烯纳米带中化学掺杂引起的半金属性能，单旋负差动电阻和大单旋塞贝克效应

通过羟基边缘官能化调节曲折形石墨烯纳米带的磁分裂

网络技术-网络基础-纳米器件中电子输运的理论研究.pdf

石墨烯纳米带的磁电子性质和载流子迁移率：理论预测

基于CORDIC的反正弦和反余弦计算的FPGA实现

最新资源