双率系统辅助模型框架下的随机牛顿递推辨识资源-CSDN文库

127 浏览量 2021-01-14 01:48:57 上传评论收藏 212KB PDF 举报

资源推荐

资源详情

资源评论

第 30 卷第 1 期

Vol. 30 No. 1

控制与决策

Control and Decision

2015 年 1 月

Jan. 2015

双率系统辅助模型框架下的随机牛顿递推辨识

文章编号: 1001-0920 (2015) 01-0117-08 DOI: 10.13195/j.kzyjc.2013.1227

曹鹏飞, 罗雄麟

(中国石油大学自动化研究所，北京 102249)

摘要: 针对双率系统, 采用基于辅助模型的改进随机牛顿递推算法辨识输出误差模型. 若当前参数估计对应的

估计系统不稳定, 则出现中间不可测时刻输出估计发散, 辨识过程停止. 增加非线性模型与常规辅助模型一起为

下步递推提供信息估计, 确保递推进行. 为避免出现输入不充分或者广泛时 Hessian 阵奇异或者接近奇异的情况,

在 Hessian 阵的递推中增加对称正定矩阵. 最后给出了所提出辨识算法的一致收敛性证明.

关键词: 双率系统；辨识；双辅助模型；收敛分析；改进随机牛顿算法

中图分类号: TP273 文献标志码: A

Auxiliary-model-based stochastic Newton recursive identiﬁcation for

dual-rate system

CAO Peng-fei, LUO Xiong-lin

(Research Institute of Automation，China University of Petroleum，Beijing 102249，China．Correspondent：LUO

Xiong-lin，E-mail：luoxl@cup.edu.cn)

Abstract: An auxiliary-model-based improved stochastic Newton recursive algorithm is utilized to identify the output-error

model for the dual-rate system. The output estimations at the time between two slow-sampled periods will diverge when

the unstable estimated system arises and the identiﬁcation process will cease. Therefore, a nonlinear model is proposed as

the sub-auxiliary model. Together with the general auxiliary model, the proposed model provides estimated information for

the next recursion. When the input is not general enough, the Hessian matrix will be singular or nearly singular. A positive

deﬁnite symmetric matrix is added to the recursion for Hessian matrix to ensure it positive deﬁnite. Finally, the uniform

convergence of the proposed algorithm is proved.

Keywords: dual-rate system；identiﬁcation；double auxiliary models；convergence analysis；improved stochastic

Newton algorithm

0 引引引言言言

由于受到客观物理因素的限制, 连续系统的输

入输出量有不同的采样频率, 从而形成了多采样频率

系统 (多率系统)

[1]

. 双率系统是一种特殊的多率系统,

其广泛存在, 并具有较强的研究意义. 双率系统控制

不仅在石油化工过程控制方面得到了成功应用, 在

理论方面也取得了一系列研究成果, 例如双率系统

自适应控制

[2]

、双率系统预测控制

[3]

、鲁棒控制

[4]

等.

而能否得到双率模型则是控制研究首要解决的问

题

[5-6]

, 因此双率系统辨识成为双率系统研究的最主

要的热点和难点之一. 一般是针对某种模型结构采

用某些辨识算法, 例如基于状态空间模型利用提升

技术辨识

[7]

、基于小波模型利用小波多分辨率分析辨

识

[8]

、基于差分方程利用多项式转换技术辨识

[9-10]

等

等.

本文主要针对快采样输入和慢采样输出的双率

系统建立输出误差模型, 并基于此模型研究辨识算法.

多项式转换技术

[9-10]

是辨识双率系统模型的主要方

法, 单率模型经过多项式技术转化为仅依赖于直接测

量数据辨识的双率模型, 并利用最小二乘算法辨识双

率模型参数和估计不可测时刻输出. 然而, 伴随更多

参数的出现, 计算量成倍增加, 因此多项式技术也存

在一定的局限性. Ding 等

[11-12]

在多项式变换后, 首先

根据递阶原理将双率模型分成多个维数较小的子系

收稿日期: 2013-09-05；修回日期: 2014-03-05.

基金项目: 国家973计划项目(2012CB720500)；国家自然科学基金项目(61104218)；中国石油大学(北京)科研基金项

目(YJRC-2013-12).

作者简介: 曹鹏飞(1988−), 男, 博士生, 从事软测量、系统辨识的研究；罗雄麟(1963−), 男, 教授, 博士生导师, 从事控

制理论、过程控制工程、化工系统工程、机器学习等研究.

118

控制与决策

第 30 卷

统, 并分别辨识各个子系统和调整子系统间的关联项.

虽然这种递阶分解的方式能够降低各个子系统的辨

识维数, 但仍无法避免大周期比 (输出与输入的采样

周期比值) 下辨识的计算量问题. Raghavan 等

[13]

提出

了期望最大化迭代算法, 根据可测数据辨识得到采样

间值, 避免了利用多项式转换技术出现大量参数的问

题. 然而, 这种插值方法只能提供一定可靠性的中间

时刻插值, 并不能完全解决大周期比情况下的辨识问

题. 丁锋等

[14-16]

提出了基于辅助模型的辨识算法, 该

方法基于可测信息建立辅助模型, 利用辅助模型输出

代替系统模型不可测变量. 通过辅助模型参变量的调

整, 使得辅助模型的输出逼近不可测变量, 最终得到

系统模型参数一致收敛.

基于辅助模型的辨识方法避免了双率模型高维

参数辨识的问题, 能够给出较好的参数一致估计, 因

此本文利用已有方法建立辅助模型, 并基于辅助模型

利用递推辨识算法估计系统模型参数. 为避免中间不

可测时刻输出估计发散影响参数收敛, 提出增加非线

性模型作为次辅助模型, 与原有辅助模型 (主辅助模

型) 一起为下步递推提供所需信息估计. 另外, 递推算

法采用改进随机牛顿算法, 在原 Hessian 矩阵递推中

增加了对称正定矩阵, 保证 Hessian 阵在输入不充分

或者广泛的情况下正定. 最后给出了基于双辅助模型

的改进随机牛顿递推辨识算法一致收敛性证明.

1 双双双辅辅辅助助助模模模型型型与与与改改改进进进随随随机机机牛牛牛顿顿顿算算算法法法的的的必必必要要要

性性性分分分析析析

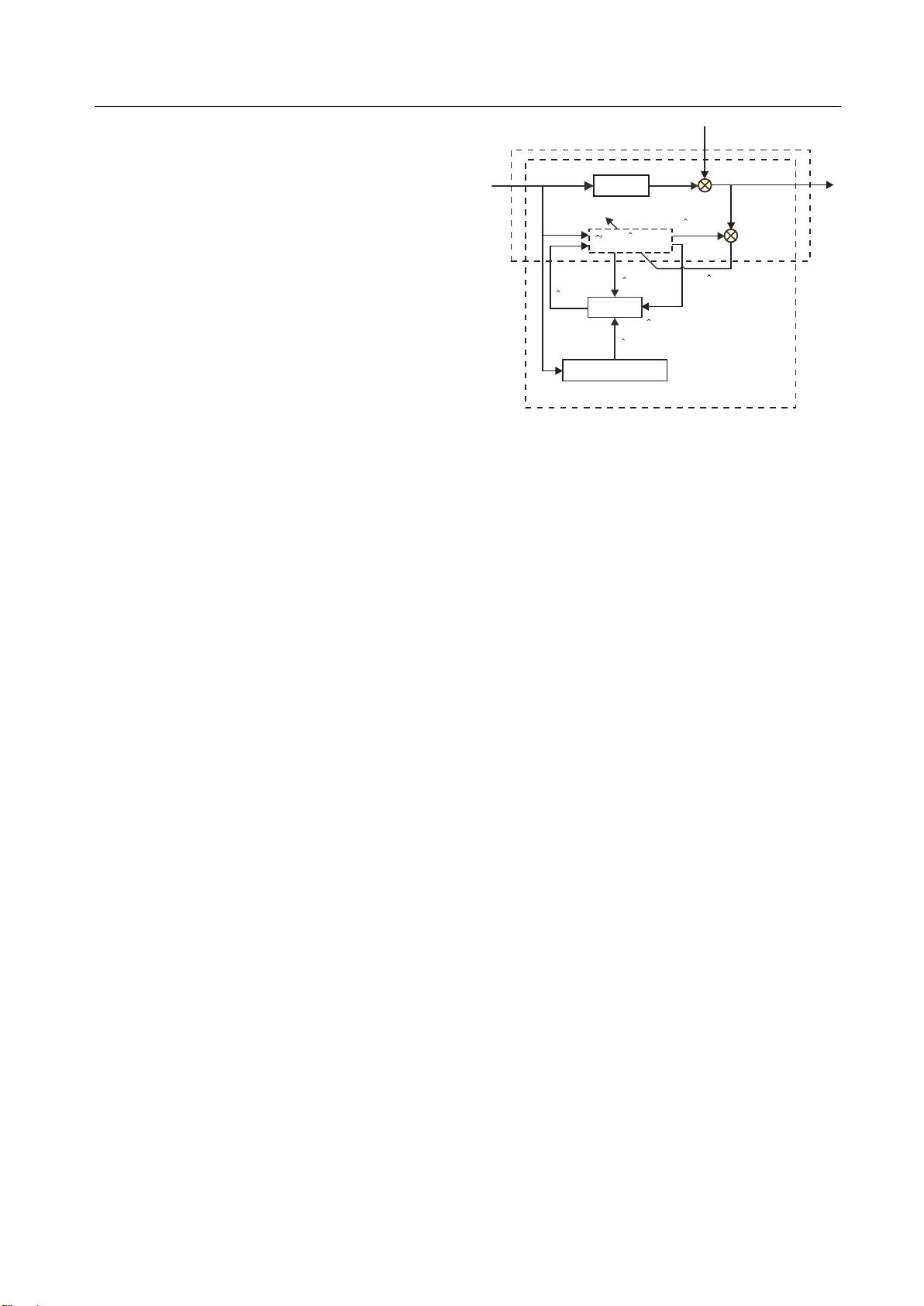
基于常规辅助模型方法辨识双率系统模型参数,

如图 1 虚线框 1 所示. 当周期比较大时, 如果在某一步

递推获得的参数估计对应的估计系统是不稳定的, 则

容易出现基于辅助模型的中间不可测时刻输出估计

的发散, 影响了递推的进行和参数的收敛. 这个问题

在最小二乘和随机梯度等经典递推算法应用在双率

辨识中同样会出现. 为了解决该问题, 本文提出增加

辅助模型的方法, 即在原有辅助模型 (主辅助模型) 基

础上增加一个非线性模型作为次辅助模型, 如图 1 虚

线框 2 所示. 两个辅助模型之间有一个切换机制, 当

主辅助模型中间不可测时刻的输出估计出现发散, 则

切换到次辅助模型, 利用次辅助模型给出下步递推所

需信息估计. 这样的方式保证了递推辨识的进行, 最

终获得参数估计一致收敛.

本文采用改进随机牛顿递推算法辨识模型. 随

机牛顿算法更加接近递推辨识算法的一般形式, 并

且以它为基础可以揭示很多辨识算法的内在联系, 如

最小二乘递推算法、梯度递推算法等

[17]

. 因此, 随机

牛顿算法是一种更加有研究价值的算法形式. 然而,

Ljung

[18]

指出, 当输入信号并不充分或者广泛时容易

process

switch

u kq( )

y kq

( )

y kq( )

v kq( )

φ( )kq

φ kq θ kq-q( ) ( )

( )kq

nonlinearmodel

!"#$%

e kq

( )

{ ( + ), =0,1,…, }y kq q i i q- ≤

&'(1

&'(2

)"#$%

图 1 递推辨识算法流程

出现 Hessian 阵奇异或者接近奇异的情况, 会影响到

参数的递推过程. 因此这里提出改进, 在 Hessian 阵的

递推中增加一个对称正定矩阵, 该矩阵在满足一定条

件下保证递推的有效进行, 并且不影响参数估计一致

收敛.

2 基基基于于于双双双辅辅辅助助助模模模型型型的的的改改改进进进随随随机机机牛牛牛顿顿顿递递递推推推

算算算法法法

2.1 改改改进进进随随随机机机牛牛牛顿顿顿递递递推推推算算算法法法

一般线性时不变系统输出误差模型可用下式表

示:

𝐴(𝑧)𝑦(𝑘) = 𝐵(𝑧)𝑢(𝑘) + 𝜐( 𝑘);

𝐴(𝑧) = 1 + 𝑎

𝑧

−1

+ ⋅ ⋅ ⋅ + 𝑎

𝑛

𝑎

𝑧

−𝑛

𝑎

𝐵(𝑧) = 𝑏

𝑧

−1

+ ⋅ ⋅ ⋅ + 𝑏

𝑛

𝑏

𝑧

−𝑛

𝑏

整理得到

𝑦(𝑘) = 𝜑

(𝑘)𝜃 + 𝜐(𝑘); (1)

𝜑

(𝑘) = [−𝑦(𝑘 − 1), −𝑦(𝑘 − 2), ⋅ ⋅ ⋅ , −𝑦 (𝑘 − 𝑛

𝑎

𝑢(𝑘 − 1), ⋅ ⋅ ⋅ , 𝑢(𝑘 − 𝑛

𝑏

)],

𝜃 = [𝑎

, 𝑎

, ⋅ ⋅ ⋅ , 𝑎

𝑛

𝑎

, 𝑏

, ⋅ ⋅ ⋅ , 𝑏

𝑛

𝑏

]

其中: 𝑦(𝑘) 为输出变量, 𝑢(𝑘) 为输入变量, 𝑣(𝑘) 为随机

噪声, 𝜑(𝑘) 被称为信息. 这里采用改进随机牛顿递推

算法辨识模型. 针对系统 (1), 具体随机牛顿参数递推

算法如下所示:

⎧



⎨



⎩

𝜃(𝑘) =

𝜃(𝑘 − 1) + 𝜌(𝑘)𝑅

−1

(𝑘)𝜑(𝑘)[𝑦(𝑘)−

𝜑

(𝑘)

𝜃(𝑘 − 1)],

𝑅(𝑘) = 𝑅(𝑘 − 1) + 𝜌(𝑘)[𝜑(𝑘)𝜑

(𝑘)−

𝑅(𝑘 − 1)].

其中: 𝜌(𝑘) 为收敛因子, 𝑅(𝑘) 为 Hessian 阵. 在 𝑅(𝑘) 的

递推公式中增加一个对称正定矩阵 𝐴(𝑘), 其在满足一

定条件下不影响参数估计的收敛结果, 具体条件在后

面收敛性证明中给出. 改进随机牛顿递推算法如下所

剩余7页未读，继续阅读

评论收藏

内容反馈

weixin_38673921

粉丝: 8
资源: 970

双率系统辅助模型框架下的随机牛顿递推辨识

DPM-IEDA：用于个人搜索的双概率模型辅助分布算法交互式估计

递推最小二乘法辨识不同阶次ARMAX模型-MATLAB实现（附带实验报告）

m文件_；模型参考_递推_系统辨识_自适应控制_

RIV辅助变量递推辨识最小二乘

递推最小二乘法及模型阶次辨识

递推最小二乘法（RLS）及模型阶次辨识（F-Test）

基于递推最小二乘法的永磁伺服系统参数辨识

基于ID=0控制的电机模型参数辨识方法：递推最小二乘法辨识定子电阻R、永磁磁链ψf及dq轴电感Ls的仿真研究,基于ID=0控制的电机模型参数辨识研究：递推最小二乘法辨识定子电阻R、永磁磁链ψf及dq轴

基于MIMO系统递推最小二乘法的参数辨识程序

用matlab实现最小二乘递推算法辨识系统参数[参照].pdf

递推最小二乘估计及模型阶次辨识

基于辅助模型的递推增广最小二乘辨识方法 (2009年)

TEST_leastsquare_递推最小二乘法_递推_在线系统辨识_在线辨识_

递推最小二乘参数辨识方法_电动车电池仿真_电动汽车动力电池SOC估算模型_电动汽车动力电池参数辨识模型_matlab仿真

递推的极大似然法辨识程序

基于MATLAB的锂离子电池二阶RC等效电路模型参数辨识研究-递推最小二乘法及其数据调整分析，附NASA官方电池数据下载地址及误差分析参考,基于MATLAB的锂离子电池二阶RC等效电路模型参数辨识研

自适应与系统辨识中增广递推最小二乘法Matlab源程序及仿真

系统辨识部分算法matlab程序

基于前向神经网络的时变非线性结构系统辨识快速递推最小二乘法.pdf

递推最小二乘估计(RLS)及模型阶次辨识(F-Test）.zip

应用最小二乘一次完成法和递推最小二乘法算法的系统辨识

bianshi.rar_RLS_模型辨识_过程辨识_递推最小二乘_递推最小二乘法

基于ID=0控制的电机模型参数辨识方法：递推最小二乘法辨识定子电阻、永磁磁链及dq轴电感的有效性仿真分析,该模型基于id=0控制 ，通过电机的基本数学模型对其定子电阻R, 永磁磁链ψf， dq轴电感L

最小二乘法系统辨识matlab代码.zip

基于递推随机子空间的电力系统低频振荡辨识.pdf

线性时变反馈系统的状态空间模型和模态参数递推辨识

递推最小二乘辨识

应用最小二乘一次完成法和递推最小二乘法算法的系统辨识word

最全系统辨识源代码，包括多种最小二乘法，极大似然法，模型阶数辨识等_最大似然估计的系统辨识程序,增广矩阵法实现系统辨识

GLS_ARARX_系统辨识；广义最小二乘_

最新资源

基于ID=0控制的电机模型参数辨识方法：递推最小二乘法辨识定子电阻、永磁磁链及dq轴电感的有效性仿真分析,该模型基于id=0控制，通过电机的基本数学模型对其定子电阻R, 永磁磁链ψf， dq轴电感L