### 弹箭气动热的数值分析概述 在现代导弹和火箭技术中,弹箭在飞行过程中的气动热现象是一个重要的研究领域。气动热,也称为气动加热,是指飞行器在高速穿越大气层时,由于与空气摩擦和压缩效应产生的热量。这些热量会使得飞行器表面温度升高,进而影响飞行器结构的完整性、弹道的准确性以及携带电子设备的功能性。因此,准确地分析弹箭在复杂边界条件下的气动热特性,对于飞行器的设计和热防护具有非常重要的意义。 ### 弹箭气动热数值分析的关键技术 #### Delaunay三角形非结构化网格 在数值分析领域,使用Delaunay三角形非结构化网格是一种常见的空间离散化技术。相对于传统的结构化网格,非结构化网格能够更灵活地适应复杂边界和几何形状的区域。通过Delaunay三角形划分,研究者可以在保持计算精度的同时,增加网格划分的自由度,以更贴近实际物体的几何外形。 #### 有限容积方法 有限容积方法(Finite Volume Method)是流体力学数值分析中的一种主要方法。其基本思想是将连续的计算区域划分为一系列控制体积,在每个控制体积上对守恒定律进行积分,从而得到离散化的控制方程。由于这种方法天然地满足守恒定律,因此在计算流体动力学领域得到了广泛应用。 #### 数值模拟程序的编写 数值模拟程序需要能够处理复杂的物理现象和各种边界条件。编写程序时,需要选择合适的编程语言和开发环境,如文中提及的可视化FORTRAN90/95语言。同时,需要考虑到计算的精度和效率,采用二阶精度格式提高结果的准确性。 #### 边界条件的处理 在非线性边界条件下进行弹箭气动热的数值分析时,需要对边界条件进行线性化处理。这包括将复杂的边界条件简化为边界温度的线性函数,以适应有限容积方法的计算要求。线性化处理涉及将边界热流密度表达为边界温度的函数,这需要通过迭代方法不断更新边界条件,以逼近实际情况。 #### 温度场分布的研究 研究不同边界条件下弹箭内部温度场的分布是弹箭气动热分析的核心内容。通过数值模拟,可以预测弹箭在不同飞行阶段、不同外部环境下的内部温度分布情况。这些信息对于设计有效的热防护措施至关重要。 ### 弹箭模型的几何形状和基本参数 弹箭模型的几何形状和基本参数决定了气动热分析的起点。文中提到的模型以长征三型火箭为基础,采用简化几何设计。弹头为单圆弧线,中间部分模拟战斗部、控制部或发动机部,尾翼部为斜三角体。这些几何参数定义了计算区域的边界,进而影响到气动热分析的准确性和复杂度。 ### 边界条件的线性化方程 在数值分析中,边界条件通常是非线性的,尤其是涉及到对流和辐射换热的复杂边界。为了在数值计算中处理这些非线性边界条件,通常需要将它们线性化。这涉及到选择合适的线性化模型,设定相关的常数项,并通过迭代方法对边界温度进行更新。 ### 结构化网格与非结构化网格的比较 在数值分析中,结构化网格和非结构化网格各有优劣。结构化网格易于编程和计算,但对于复杂几何形状的适应性较差;而非结构化网格虽然编程和计算复杂度较高,却能够更好地适应复杂的几何形状。文中通过将两种网格的计算结果进行比较,展示了非结构化网格在处理复杂边界条件时的有效性。 ### 弹箭数值计算的实例分析 文章最后给出了弹箭在不同边界条件下内部温度场分布的数值计算实例。通过设定头部和尾翼为对流和辐射的边界条件,可以模拟弹箭在实际飞行过程中的热传导情况。通过对比不同网格下的温度分布,验证了程序计算的正确性和可靠性。 ### 结论 通过上述分析,本文展示了在不同边界条件下,使用Delaunay三角形非结构化网格和有限容积方法对弹箭气动热进行数值分析的过程和结果。研究结果表明,所采用的方法和程序能够有效地模拟弹箭在复杂边界条件下的内部温度场分布,对于弹箭的热防护设计具有重要的参考价值。同时,通过与结构化网格的对比,进一步证明了非结构化网格在处理复杂边界问题时的优越性。

- 粉丝: 6
- 资源: 910
 我的内容管理
展开
我的内容管理
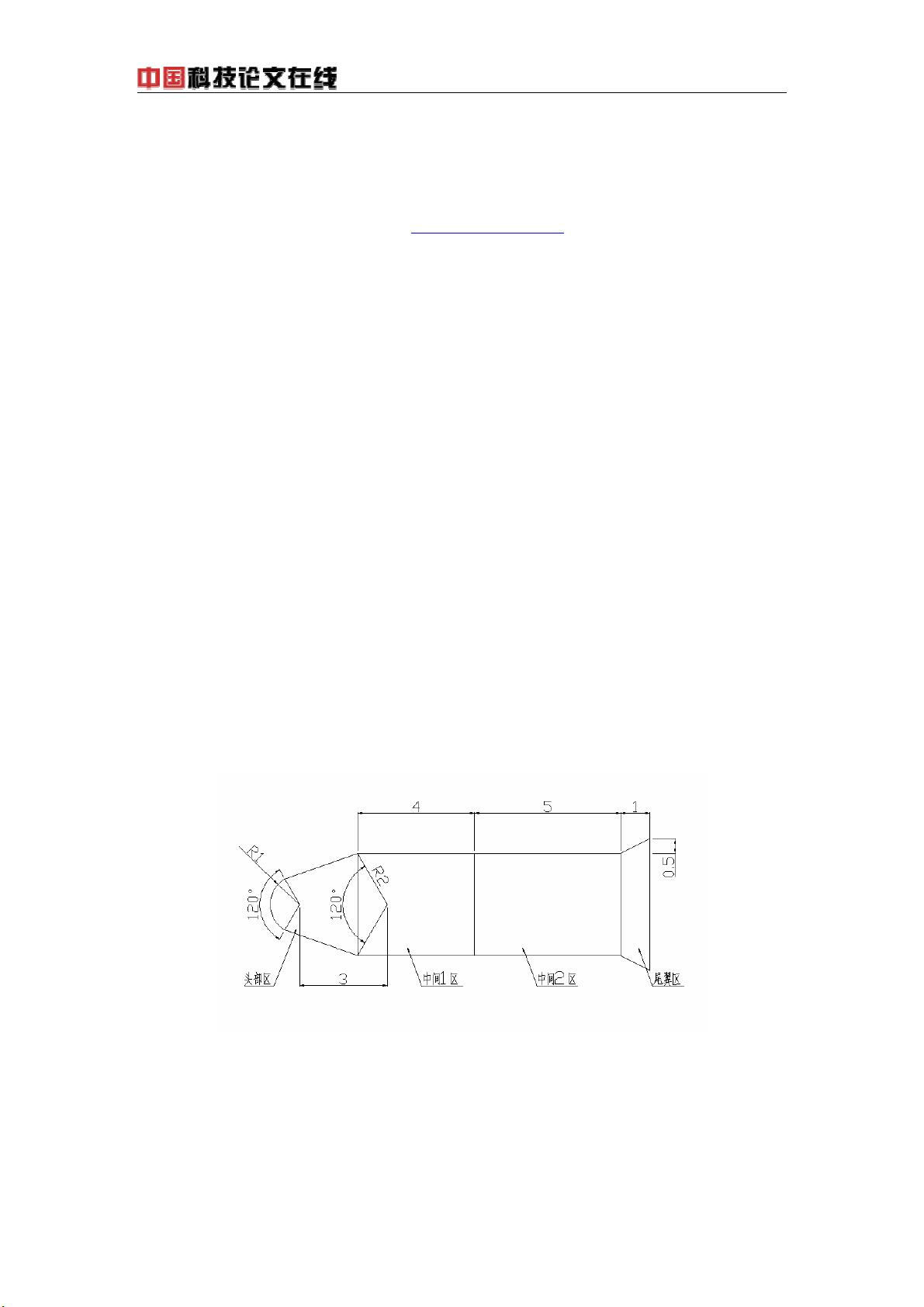
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功