使用稀疏性以外的先验信息进行多变量追踪图像重建

47 浏览量 2021-03-10 13:37:41 上传评论收藏 1.42MB PDF 举报

资源推荐

资源详情

资源评论

Multivariate pursuit image reconstruction using prior

information beyond sparsity

Jiao Wu

a,b,c,

, Fang Liu

a,b

, Lc Jiao

, Xiaodong Wang

a,b

School of Computer Science and Technology, Xidian University, Xi’an 710071, PR China

Key Laboratory of Intelligent Perception and Image Understanding of Ministry of School of Computer Science and Technology,

Xidian University, Xi’an 710071, PR China

College of Sciences, China Jiliang University, Hangzhou 310018, PR China

article info

Article history:

Received 25 January 2012

Received in revised form

10 September 2012

Accepted 16 September 2012

Available online 26 September 2012

Keywords:

Compressive sensing

Edge detection

Prior model

Wavelet transform

abstract

The prior information of images plays an important role in reducing the computational

complexity of CS inversion and improving the reconstruction quality. A wavelet-based

multivariate pursuit algorithm, which exploits the prior information of images that goes

beyond simple sparsity, is developed in this paper. The proposed method reconstructs the

image wavelet coefﬁcients from the multiple measurements in a multivariate manner, and

uses the extracted image edge as the prior information to guide the pursuit process of

algorithm in CS recovery. By means of the interaction of edge information and multivariate

joint recovery, the proposed algorithm signiﬁcantly improves the reconstruction quality

of those images with the obvious edges and high sparsity, such as CT, MRI images. Numerical

experiments demonstrate that the proposed algorithm returns superior reconstructed

quality and remains higher computational efﬁciency than other stat e-of-the-art CS

algorithms.

1. Introduction

Compressive sensing (CS) [1,2] demonstrates that sparse

images can be recovered from fewer random measure-

ments by taking advantage of the sparsity inherent in

real world images. In other words, if an image f 2

can be converted into one having relatively few values

signiﬁcantly different from zero under a certain orthogonal

transform

MM

,thatisf ¼

x, one may reconstruct

the transform coefﬁcient vector x from fewer linear mea-

surements of f by solving the following l

-problem:

min

JxJ

s:t: y ¼

f ¼

x, ð1Þ

where y 2

ðK 5MÞ is the linear measurements of f under

the given measurement matrix

KM

,and

However, l

-problem is NP-hard . Thus designing the

effective and low computational complexity CS reconstruc-

tion method is of great signiﬁcance.

Theorthogonalbasisforsparserepresentationofimages

is one of the key factors of CS, with the wavelet transform [3]

being an important exampl e. Under the wavele t transform,

the main energ y of image is concentrated in the low

frequency part, and the singularity characteristics show the

signiﬁcant sparsity in the high frequency parts, that is, the

wavelet coefﬁcients that correspond to the edge and ridge

are signiﬁcan tly differe nt from zero. G eneral ly, there ar e

some particular structures (such as the tree structure and

Contents lists available at SciVerse ScienceDirect

journal homepage: www.elsevier.com/locate/sigpro

Signal Processing

http://dx.doi.org/10.1016/j.sigpro.2012.09.010

This work was supported in part by the National Natural Science

Foundation of China (Grant nos. 60971112, 60971128, 60970067,

61072106, 61072108, 61173090), in part by the Fund for Foreign Scholars

in University Research and Teaching Programs (the 111 Project) (Grant no.

B07048), in part by the Program for Cheung Kong Scholars and Innovative

Research Team in University (Grant no. IRT1170), and in part by the Funded

By Open Research Fund Program of Key Lab of Intelligent Perception and

Image Understanding of Ministry of Education of China (Grant no.

IPIU012011002).

Corresponding author at: School of Computer Science and Technol-

ogy, Xidian University, Xi’an 710071, PR China.

E-mail addresses: wu_jiao@yahoo.cn (J. Wu),

lf204310@163.com (F. Liu), jlc1023@163.com (L. Jiao),

xdwang@mail.xidian.edu.cn (X. Wang).

Signal Processing 93 (2013) 1662–1672

the dependence structure) within the wavelet coefﬁcients of

images. The expl icit use of these structures has appeared in

image compressi on and denoi sing proble ms [4–9].

A multiscale CS scheme [10] is developed based on the

multiscale decomposition by using conventional linear

sampling and reconstruction for low frequency information,

and compressed sampling on high frequency information.

Under this framework, more realistic prior information

(such as tree structures and dependencies of image wavelet

coefﬁcients) can be exploited to wavelet-based CS recovery.

Examples of such techniques include the tree structure-

based methods [11–16] and the dependence structure-

based method [17]. The tree-based approaches enforce

the additional tree-structured dependencies in CS recovery

by exploiting the sparse tree representation or HMT mod-

els. In our previous work [17], the developed multivariate

pursuit algorithm (MPA) jointly recovers the wavelet coef-

ﬁcients of images from the multiple CS measurements by

integrating the statistical dependence models of wavelet

neighborhood coefﬁcients in CS recovery. In addition, the

edge also is one of the important prior information which

exists in the image to be recovered. As mentioned above,

under the wavelet transform, the edges of i mage corre-

spond to those non-zero wavelet coefﬁcients to be recov-

ered. An edge guided MRI recovery algorithm in Fourier

domain [18] produces the state-of-art reconstruction

results by performing an iterative reweighed TV norm

minimization where the weights are dependent on edge

information. The theoretical and numerical results of the

aforementioned methods demonstrate that the superior

performance can be obtained with the fewer measurements

by leveraging the prior models of images.

The purpose of this paper is to design an edge-based

multivariate pursuit algorithm (EMPA) for wavelet-based

CS reconstruction of images. The developed algorithm can

be viewed as an improvement of MPA. The main con-

tributions of this paper are as follows:



Under multiscale CS framework, the multivariate CS

sampling scheme [17] is used to make the multiple CS

measurements, then the reconstruction problem of

images from CS is converted to a sparse multiple

measurement vectors (MMV) problem [19–23], while

the traditional CS corresponds to the single measure-

ment vector (SMV) problem. The theoretical analysis

[20,23] demonstrates that the performance of jointly

sparse recovery for MMV is higher than that of SMV

with the fewer measurements.



MPA solves MMV problem by successively estimating

the wavelet coefﬁcients in neighborhoods and itera-

tively updating the residuals. However, in this manner

the supports of coefﬁcients (i.e. the location of non-

zero coefﬁcients) cannot be identiﬁed, that is to say,

the sparse solution of MMV problem cannot be cor-

rectly recovered. To this end, we design an extraction

scheme of image edge information from the complete

low frequency measurements, and use the extracted

edge information as the prior of coefﬁcient supports to

guide the pursuit process of MPA, thus obtain the

sparse solution of MMV problem.



The combination of multivariate joint recovery and edge

information guide contributes a lot to the improvement of

reconstruction performance, especially for those images

with the obvious edges and hi gh sparsity, such as CT, MRI

images.



As the incorporation of image edge information requires

edge detection step, comparing with MPA, the running

time of EMPA increases slightly. However, EMPA has

higher computational efﬁciency than many other state-

of-the-art CS algorithms.

The remainder of this paper is organized as follows.

Section 2 reviews the multivariate compressive sample

scheme and describe s the prob lem formulat ion. The idea

and main procedu re of MPA is reviewed in Section 3.In

Section 4, we ﬁrst give the general framework of EMPA and

detail how to extract edge information from CS measure-

ments. Then we interpret how to use the edge information to

guide MPA in CS recovery, thus derive EMPA and several vari-

ant algorithms. Section 5 reports the experimental results.

Conclusions and future work are discussed in Section 6.

2. Multivariate compressive sampling and problem

formulation

2.1. Multivariate compressive sampling

A multivariate compressive sampling scheme [17] has

been designed for taking multiple CS measurements. This

method ﬁrst rearranges the wavelet coefﬁcients according

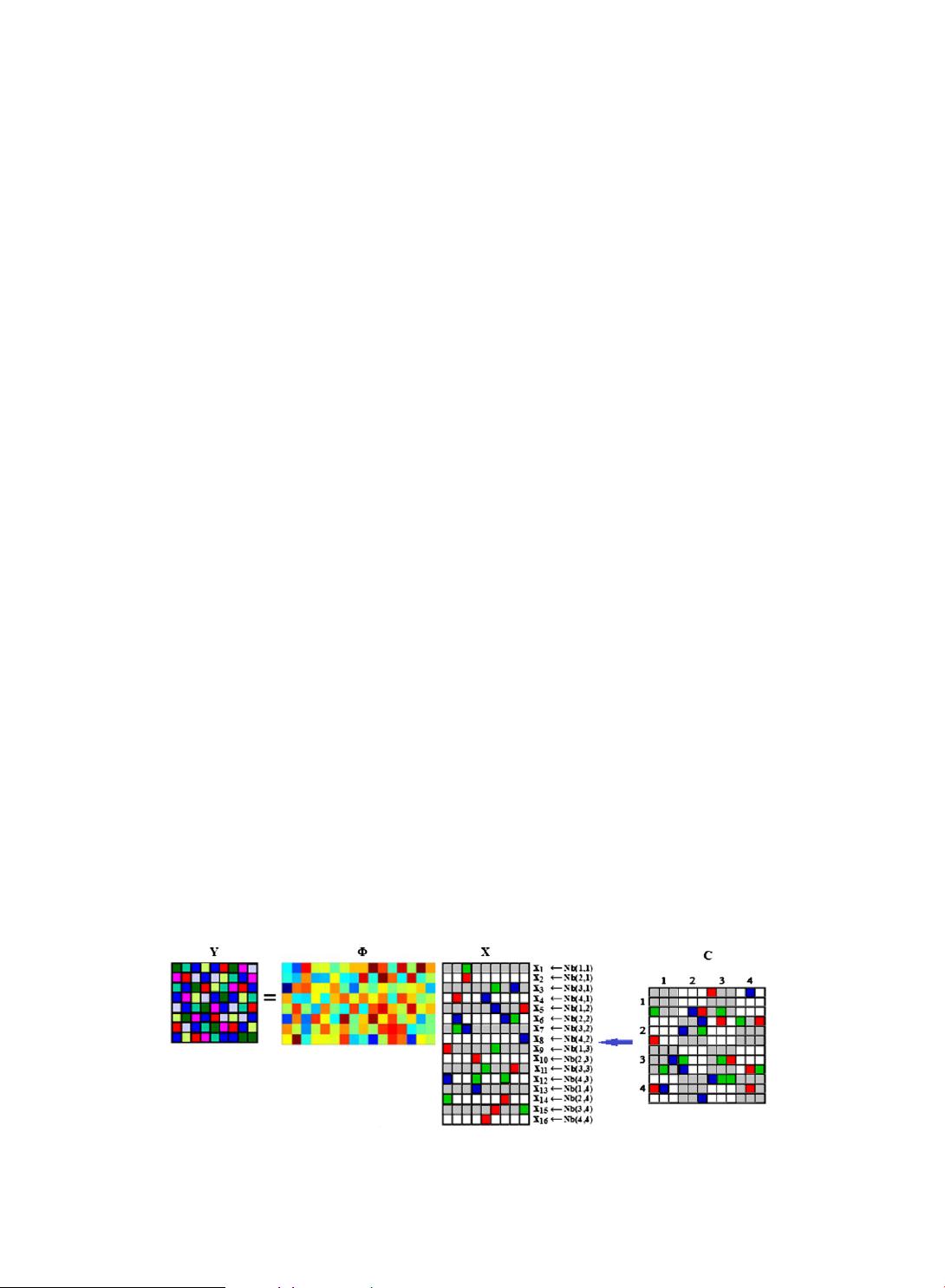
Fig. 1. Example of multivariate CS sampling. Given the size of small neighborhood 3 3, a 12 12 image coefﬁcient matrix C (in the right) is partitioned

into 16 small neighborhoods. The ðj

, j

Þth small neighborhood Nbðj

, j

Þðj

, j

¼1, 2, 3, 4Þ is represented as a 9-dimension vector x

¼ðx

, ...,

ði ¼ j

þ4 ðj

1ÞÞ. Then C is represented as a 16 9 multivariate coefﬁcient matrix X ¼ðx

, ..., x

. With an 8 16 measurement matrix

,an

8 9 multiple measurement matrix is taken as Y ¼

J. Wu et al. / Signal Processing 93 (2013) 1662–1672 1663

剩余10页未读，继续阅读

评论收藏

内容反馈

weixin_38654944

粉丝: 2
资源: 943

使用稀疏性以外的先验信息进行多变量追踪图像重建

【图像重建】基于Split Bregman实现稀疏图像重建附matlab代码 上传版本.zip

梯度稀疏性先验图像matting算法

基于稀疏支撑集先验的压缩感知图像序列重建算法.docx

论文研究-基于稀疏与低秩的核磁共振图像重构算法.pdf

从具有先验信息的无人机图像进行批量重建

中心先验.rar_object detection_图像先验_显著性_显著性先验_显著性检测中心先验

电信设备-先验信息传导的序列立体图像匹配方法.zip

基于全面稀疏先验的MR图像重建

使用强大的稀疏先验图像去模糊

暗原色先验图像去雾算法研究

有限角度CT图像重建迭代算法研究1

Qt 5实现串口调试助手 （源工程文件、0积分下载）

【SystemVerilog】路科验证V2学习笔记（全600页）.pdf

AutoSAR标准协议4.2.2

光伏-储能并网系统仿真.rar

XCP协议的规范文档

GD32替换STM32注意事项.pdf

NPPJSONViewer.zip

蓝牙BLE协议中文版.pdf

CANoe通过CAPL脚本实现自动测试

AD20官方中文教程.pdf

最新资源

【图像重建】基于Split Bregman实现稀疏图像重建附matlab代码上传版本.zip

Qt 5实现串口调试助手（源工程文件、0积分下载）