没有合适的资源?快使用搜索试试~ 我知道了~
温馨提示
Rethinking SIMD Vectorization for In-Memory DatabasesOrestis Polychroniou∗ Columbia Universityorestis@cs.columbia.eduArun Raghavan Oracle Labsarun.raghavan@oracle.comKenneth A. Ross† Columbia Universitykar@cs.columbia.eduABSTRACT Analytical databases are continuously adapting to the un- derlying hardware in order to saturate all sources of par- allelism. At the same time, hardware evolves in multiple directions to explore different trade-offs. The MIC architec- ture, one such example, strays fro
资源推荐
资源详情
资源评论

Rethinking SIMD Vectorization for In-Memory Databases
Orestis Polychroniou
∗
Columbia University
orestis@cs.columbia.edu
Arun Raghavan
Oracle Labs
arun.raghavan@oracle.com
Kenneth A. Ross
†
Columbia University
kar@cs.columbia.edu
ABSTRACT
Analytical databases are continuously adapting to the un-
derlying hardware in order to saturate all sources of par-
allelism. At the same time, hardware evolves in multiple
directions to explore different trade-offs. The MIC architec-
ture, one such example, strays from the mainstream CPU
design by packing a larger number of simpler cores per chip,
relying on SIMD instructions to fill the performance gap.
Databases have been attempting to utilize the SIMD ca-
pabilities of CPUs. However, mainstream CPUs have only
recently adopted wider SIMD registers and more advanced
instructions, since they do not rely primarily on SIMD for
efficiency. In this paper, we present novel vectorized designs
and implementations of database operators, based on ad-
vanced SIMD operations, such as gathers and scatters. We
study selections, hash tables, and partitioning; and com-
bine them to build sorting and joins. Our evaluation on the
MIC-based Xeon Phi co-processor as well as the latest main-
stream CPUs shows that our vectorization designs are up to
an order of magnitude faster than the state-of-the-art scalar
and vector approaches. Also, we highlight the impact of ef-
ficient vectorization on the algorithmic design of in-memory
database operators, as well as the architectural design and
power efficiency of hardware, by making simple cores com-
parably fast to complex cores. This work is applicable to
CPUs and co-processors with advanced SIMD capabilities,
using either many simple cores or fewer complex cores.
1. INTRODUCTION
Real time analytics are the steering wheels of big data
driven business intelligence. Database customer needs have
extended beyond OLTP with high ACID transaction through-
put, to interactive OLAP query execution across the entire
database. As a consequence, vendors offer fast OLAP solu-
tions, either by rebuilding a new DBMS for OLAP [28, 37],
or by improving within the existing OLTP-focused DBMS.
∗
Work partly done when first author was at the Oracle Labs.
†
Supported by NSF grant IIS-1422488 and an Oracle gift.
Permission to make digital or hard copies of all or part of this work for personal or
classroom use is granted without fee provided that copies are not made or distributed
for profit or commercial advantage and that copies bear this notice and the full cita-
tion on the first page. Copyrights for components of this work owned by others than
ACM must be honored. Abstracting with credit is permitted. To copy otherwise, or re-
publish, to post on servers or to redistribute to lists, requires prior specific permission
and/or a fee. Request permissions from permissions@acm.org.
SIGMOD ’15, May 31 - June 04, 2015, Melbourne, VIC, Australia.
Copyright 2015 ACM 978-1-4503-2758-9/15/05 ...$15.00.
http://dx.doi.org/10.1145/2723372.2747645.
The advent of large main-memory capacity is one of the
reasons that blink-of-an-eye analytical query execution has
become possible. Query optimization used to measure blocks
fetched from disk as the primary unit of query cost. Today,
the entire database can often remain main-memory resident
and the need for efficient in-memory algorithms is apparent.
The prevalent shift in database design for the new era
are column stores [19, 28, 37]. They allow for higher data
compression in order to reduce the data footprint, minimize
the number of columns accessed per tuple, and use column
oriented execution coupled with late materialization [9] to
eliminate unnecessary accesses to RAM resident columns.
Hardware provides performance through three sources of
parallelism: thread parallelism, instruction level parallelism,
and data parallelism. Analytical databases have evolved to
take advantage of all sources of parallelism. Thread par-
allelism is achieved, for individual operators, by splitting
the input equally among threads [3, 4, 5, 8, 14, 31, 40],
and in the case of queries that combine multiple operators,
by using the pipeline breaking points of the query plan to
split the materialized data in chunks that are distributed to
threads dynamically [18, 28]. Instruction level parallelism is
achieved by applying the same operation to a block of tu-
ples [6] and by compiling into tight machine code [16, 22].
Data parallelism is achieved by implementing each operator
to use SIMD instructions effectively [7, 15, 26, 30, 39, 41].
The different sources of parallelism were developed as a
means to deliver more performance within the same power
budget available per chip. Mainstream CPUs have evolved
on all sources of parallelism, featuring massively superscalar
pipelines, out-of-order execution of tens of instructions, and
advanced SIMD capabilities, all replicated on multiple cores
per CPU chip. For example, the latest Intel Haswell ar-
chitecture issues up to 8 micro-operations per cycle with
192 reorder buffer entries for out-of-order execution, 256-bit
SIMD instructions, two levels of private caches per core and
a large shared cache, and scales up to 18 cores per chip.
Concurrently with the evolution of mainstream CPUs, a
new approach on processor design has surfaced. The design,
named the many-integrated-cores (MIC) architecture, uses
cores with a smaller area (transistors) and power footprint
by removing the massively superscalar pipeline, out-of-order
execution, and the large L3 cache. Each core is based on a
Pentium 1 processor with a simple in-order pipeline, but
is augmented with large SIMD registers, advanced SIMD
instructions, and simultaneous multithreading to hide load
and instruction latency. Since each core has a smaller area
and power footprint, more cores can be packed in the chip.

The MIC design was originally intended as a GPU [33],
but now targets high performance computing applications.
Using a high FLOPS machine to execute compute-intensive
algorithms with superlinear complexity is self-evident. Ex-
ecuting analytical queries in memory, however, consists of
data-intensive linear algorithms that mostly “move” rather
than“process”data. Previous work to add SIMD in databases
has optimized sequential access operators such as index [41]
or linear scans [39], built multi-way trees with nodes that
match the SIMD register layout [15, 26], and optimized spe-
cific operators, such as sorting [7, 11, 26], by using ad-hoc
vectorization techniques, useful only for a specific problem.
In this paper, we present good design principles for SIMD
vectorization of main-memory database operators, without
modifying the logic or the data layout of the baseline scalar
algorithm. The baseline algorithm is defined here as the
most straightforward scalar implementation. Formally, as-
sume an algorithm that solves a problem with optimal com-
plexity, its simplest scalar implementation, and a vectorized
implementation. We say that the algorithm can be fully vec-
torized, if the vector implementation executes O(f (n)/W )
vector instructions instead of O(f(n)) scalar instructions
where W is the vector length, excluding random memory
accesses that are by definition not data-parallel. We define
fundamental vector operations that are frequently reused
in the vectorizations and are implemented using advanced
SIMD instructions, such as non-contiguous loads (gathers)
and stores (scatters). The fundamental operations that are
not directly supported by specific instructions can be imple-
mented using simpler instructions at a performance penalty.
We implement vectorized operators in the context of main-
memory databases: selection scans, hash tables, and parti-
tioning, which are combined to build more advanced opera-
tors: sorting and joins. These operators cover a large por-
tion of the time needed to execute analytical queries in main
memory. For selection scans, we show branchless tuple selec-
tion and in-cache buffering. For hash tables, we study both
building and probing across using multiple hashing schemes.
For partitioning, we describe histogram generation, includ-
ing all partitioning function types: radix, hash, and range.
We also describe data shuffling, including inputs larger than
the cache. All of the above are combined to build radixsort
and multiple hash join variants that highlight the impact of
vectorization on determining the best algorithmic design.
We compare our vectorized implementations of in-memory
database operators against the respective state-of-the-art
scalar and vector techniques, by evaluating on the Intel Xeon
Phi co-processor and on the latest mainstream CPUs. Xeon
Phi is currently the only available hardware based on the
MIC architecture and is also the only generally available
hardware that supports gathers and scatters, while the lat-
est mainstream CPUs (Intel Haswell) support gathers.
We use the sorting and join operator to compare a Xeon
Phi 7120P co-processor (61 P54C cores at 1.238 GHz, 300
Watts TDP) against four high-end Sandy Bridge CPUs (4×8
Sandy Bridge cores at 2.2 GHz, 4 × 130 Watts TDP), and
found that they have similar performance, but on a different
power budget, since Xeon Phi spends almost half the energy.
The next generation of Xeon Phi will also be available as
a standalone CPU,
1
even if the current generation is only
1
newsroom.intel.com/community/intel_newsroom/blog/2014/
06/23/intel-re-architects-the-fundamental-building-
block-for-high-performance-computing
available as a co-processor, and will support more advanced
SIMD instructions (AVX 3), also supported by the next gen-
eration of mainstream CPUs.
2
Our work does not focus on
evaluating Xeon Phi as a co-processing accelerator, such as
GPUs, that would also be bound by the PCI-e bandwidth,
but as an alternative CPU design that is suitable and more
power efficient for executing analytical database workloads.
We summarize our contributions:
• We introduce design principles for efficient vectoriza-
tion of in-memory database operators and define fun-
damental vector operations that are frequently reused.
• We design and implement vectorized selection scans,
hash tables, and partitioning, that are combined to
design and build sorting and multiple join variants.
• We compare our implementations against state-of-the-
art scalar and vectorized techniques. We achieve up
to an order of magnitude speedups by evaluating on
Xeon Phi as well as on the latest mainstream CPUs.
• We show the impact of vectorization on the algorith-
mic design of in-memory operators, as well as the ar-
chitectural design and power efficiency of hardware, by
making simple cores comparably fast to complex cores.
The rest of the paper is organized as follows. Section 2
presents related work. Sections 4, 5, 6, and 7 discuss the
vectorization of selection scans, hash tables, Bloom filters,
and partitioning. Sections 8 and 9 discuss algorithmic de-
signs for sorting and hash join. We present our experimental
evaluation in Section 10, we discuss how SIMD vectorization
relates to GPUs in Section 11, and conclude in Section 12.
Implementation details are provided in the Appendix.
2. RELATED WORK
Previous work that added SIMD instructions in database
operators is briefly summarized. Zhou et al. used SIMD for
linear scans, index scans, and nested loop joins [41]. Ross
proposed probing multiple keys per bucket for cuckoo hash-
ing [30]. Willhalm et al. optimized decompression of bit
packed data [39]. Inoue et al. proposed data-parallel comb-
sort and merging [11]. Chhugani et al. optimized bitonic
merging for mergesort [7]. Kim et al. designed multi-way
trees tailored to the SIMD layout [15]. Polychroniou et
al. discussed trade-offs for updating heavy hitter aggregates
[25], fast range partitioning via a range function index [26],
and Bloom filter probing using gathers [27]. Schlegel et al.
described scalable frequent itemset mining on Xeon Phi [32].
Database operators have been extensively optimized for
modern processors. Manegold et al. introduced hash joins
with cache-conscious partitioning [19], which Kim et al. ex-
tended to multi-core CPUs and compared against SIMD
sort-merge joins [14]. Cieslewicz et al. and Ye et al. studied
contention-free aggregation [8, 40]. Blanas et al. and Balke-
sen et al. evaluated hardware-tuned hash joins [3, 5]. Albu-
tiu et al. introduced NUMA-aware joins and Balkesen et al.
evaluated join variants on multiple CPUs [1, 4]. Satish et al.
and Wassenberg et al. introduced buffered partitioning for
radixsort [31, 38]. Polychroniou et al. introduced in-place
and range partitioning for sorting variants [26]. Jha et al.
optimized hash joins on Xeon Phi, but used SIMD partially
only to compute hash functions and load hash buckets [12].
2
software.intel.com/blogs/2013/avx-512-instructions
Compilers partially transform scalar to SIMD code based
on loop unrolling [17] and control flow predication [34]. Our
designs are far more complicated and not strictly equivalent.
Database operators can be compiled directly [22], thus man-
ual vectorization is also desirable to maximize performance.
GPUs have also been used in databases for generic queries
[2] and to accelerate operators, such as indexes [15], sorting
[31], joins [13, 24], and selections [36]. SIMT GPU threads
are organized in warps that execute the same scalar instruc-
tion per cycle by predicating all control flow. In SIMD code,
control flow is converted to data flow in software. We discuss
the similarities between SIMD and SIMT code and to what
extent our work is applicable to SIMT GPUs in Section 11.
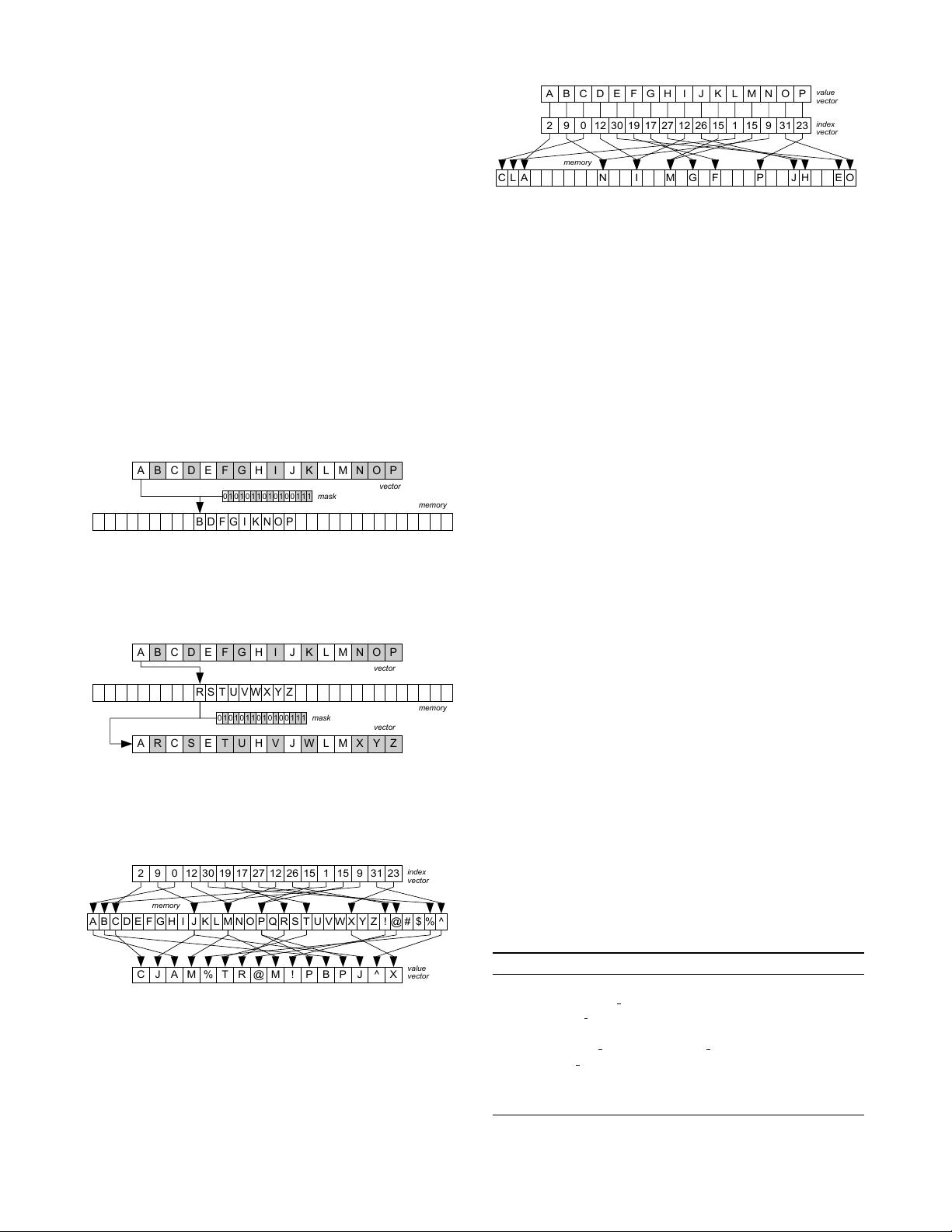
3. FUNDAMENTAL OPERATIONS
In this section we define the fundamental vector opera-
tions that we will need to implement vectorized database
operators. The first two operations, termed selective load
and selective store, are spatially contiguous memory accesses
that load or store values using a subset of vector lanes. The
last two operations are spatially non-contiguous memory
loads and stores, termed gathers and scatters respectively.
A B C D E F G H I J K L M N O P
B D F G I K N O P
0 1 0 1 0 1 1 0 0 1 0 0 1 1 1
vector
memory
mask
Figure 1: Selective store operation
Selective stores write a specific subset of the vector lanes
to a memory location contiguously. The subset of vector
lanes to be written is decided using a vector or scalar register
as the mask, which must not be limited to a constant.
A B C D E F G H I J K L M N O P
R S T U V W X Y Z
0 1 0 1 0 1 1 0 1 0 1 0 0 1 1 1
A R C S E T U H V J W L M X Y Z
vector
vector
mask
memory
Figure 2: Selective load operation
Selective loads are the symmetric operation that involves
loading from a memory location contiguously to a subset of
vector lanes based on a mask. The lanes that are inactive
in the mask retain their previous values in the vector.
C J A M % T R @ M ! P B P J ^ X
2 9 0 12 30 19 17 27 12 26 15 1 15 9 31 23
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z ! @ # $ % ^
memory
index
vector
value
vector
Figure 3: Gather operation
Gather operations load values from non-contiguous loca-
tions. The inputs are a vector of indexes and an array
pointer. The output is a vector with the values of the respec-
tive array cells. By adding a mask as an input operand, we
define the selective gather that operates on a subset of lanes.
The inactive mask lanes retain their previous contents.
A B C D E F G H I J K L M N O P
2 9 0 12 30 19 17 27 12 26 15 1 15 9 31 23
C L A N I M G F P J H E O
memory
value
vector
index
vector
Figure 4: Scatter operation
Scatter operations execute stores to multiple locations.
The input is a vector of indexes, an array pointer, and a
vector of values. If multiple vector lanes point to the same
location, we assume that the rightmost value will be written.
By adding a mask as an input we can store lanes selectively.
Gathers and scatters are not really executed in parallel
because the (L1) cache allows one or two distinct accesses
per cycle. Executing W cache accesses per cycle is an im-
practical hardware design. Thus, random memory accesses
have to be excluded from the O(f(n)/W ) vectorization rule.
Gathers are supported on the latest mainstream CPUs
(Haswell) but scatters are not. Older mainstream CPUs
(e.g., Sandy Bridge) support neither. Emulating gathers is
possible at a performance penalty, which is small if done
carefully. We discuss more hardware details in Appendix B.
Selective loads and stores are also not supported on the
latest mainstream CPUs, but can be emulated using vector
permutations. The lane selection mask is extracted as a
bitmask and is used as an array index to load a permutation
mask from a pre-generated table. The data vector is then
permuted in a way that splits the active lanes of the mask
to the one side of the register and the inactive lanes to the
other side. In case of a selective store we can store the vector
(unaligned) and in case of a selective load, we load a new
vector (unaligned) and blend the two vectors to replace the
inactive lanes. This technique was first used in vectorized
Bloom filters [27] on CPUs, without defining the operations.
We describe the Xeon Phi instructions in Appendix C.
4. SELECTION SCANS
Selection scans have re-emerged for main-memory query
execution and are replacing traditional unclustered indexes
in modern OLAP DBMSs [28]. Advanced optimizations in-
clude lightweight bit compression [39] to reduce the RAM
bandwidth, generation of statistics to skip data regions [28],
and scanning of bitmaps-zonemaps to skip cache lines [35].
Linear selective scan performance has been associated with
branch mispredictions, if the operator is implemented as
shown in Algorithm 1. Previous work has shown that con-
verting control flow to data flow can affect performance,
making different approaches optimal per selectivity rate [29].
Branches can be eliminated as shown in Algorithm 2 to avoid
misprediction penalties, at the expense of accessing all pay-
load columns and eagerly evaluating all selective predicates.
Algorithm 1 Selection Scan (Scalar - Branching)
j ← 0 output index
for i ← 0 to |T
keys in
| − 1 do
k ← T
keys in
[i] access key columns
if (k ≥ k
lower
) && (k ≤ k
upper
) then short circuit and
T
payloads out
[j] ← T
payloads in
[i] copy all columns
T
keys out
[j] ← k
j ← j + 1
end if
end for
剩余15页未读,继续阅读
资源评论

weixin_38653687
- 粉丝: 3
- 资源: 973
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 基于springboot+Vue的老年一站式服务平台(Java毕业设计,附源码,部署教程).zip
- 杭州衡泰软件实施工程师面试问题docx
- 基于SpringBoot+Vue的老年人体检管理系统(Java毕业设计,附源码,部署教程).zip
- 基于SpringBoot+Vue的老年人体检管理系统2(Java毕业设计,附源码,部署教程).zip
- 基于springboot+Vue的科研项目验收管理系统(Java毕业设计,附源码,部署教程).zip
- 基于springboot+Vue的库存管理系统2(Java毕业设计,附源码,部署教程).zip
- 基于springboot+Vue的库存管理系统(Java毕业设计,附源码,部署教程).zip
- 基于springboot+Vue的酒店管理系统(Java毕业设计,附源码,部署教程).zip
- 基于SpringBoot+Vue的开发的精简博客系统的设计与实现(Java毕业设计,附源码,部署教程).zip
- 基于springboot+Vue的经方药食两用服务平台(Java毕业设计,附源码,部署教程).zip
- 堪培拉天气数据集.zip
- 基于springboot+Vue的交通管理在线服务系统的开发2(Java毕业设计,附源码,部署教程).zip
- 基于springboot+Vue的教学资料管理系统(Java毕业设计,附源码,部署教程).zip
- 基于springboot+Vue的教学资料管理系统2(Java毕业设计,附源码,部署教程).zip
- 基于SpringBoot+Vue的家政服务平台的设计与实现2(Java毕业设计,附源码,部署教程).zip
- 基于SpringBoot+Vue的家政服务平台的设计与实现(Java毕业设计,附源码,部署教程).zip
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功