没有合适的资源?快使用搜索试试~ 我知道了~
我们研究了非阿贝尔T-对偶性(NATD)对II型超重力D膜解决方案的影响。 完整的皮套解决方案的知识使我们能够跟踪皮套装料和相应的皮套配置,从而为文献中先前提出的皮套设置以及Dp皮套解决方案产生D(p + 1)-D的常见知识提供理由 (p + 3)-NS5背景在SU(2)NATD下横向于麸皮。 在时空为空且在NATD之前的空间无穷处平坦的Brane解决方案中,NATD的空间无穷是通用的,即与初始Brane配置无关。 此外,它提供了足够的信息来确定NATD之后所有坐标的范围。 在这里考虑的更复杂的D2黄铜示例中,时空在NATD之前不是渐近平缓的,对偶解的解释仍然不清楚。 在Sasaki-Einstein 7流形上将M2还原为IIA而产生的超对称D2黄铜的情况下,我们明确验证了该解在四个维度上都服从了适用于超对称畴壁的适当广义Spinor方程。 我们还研究了超对称质量变形D2麸解决方案的存在。
资源推荐
资源详情
资源评论

Available online at www.sciencedirect.com
ScienceDirect
Nuclear Physics B 947 (2019) 114733
www.elsevier.com/locate/nuclphysb
D-branes and non-Abelian T-duality
Robin Terrisse
a
, Dimitrios Tsimpis
a,∗
, Catherine A. Whiting
b,c
a
Institut de Physique Nucléaire de Lyon, Université de Lyon, UCBL, UMR 5822, CNRS/IN2P3, 4 rue Enrico Fermi,
69622 Villeurbanne Cedex, France
b
National Institute for Theoretical Physics, School of Physics and Mandelstam Institute for Theoretical Physics,
University of the Witwatersrand, Johannesburg, WITS 2050, South Africa
c
Department of Physics and Astronomy, Bates College, Lewiston, ME 04240, USA
Received 7
February 2019; received in revised form 24 July 2019; accepted 12 August 2019
Available
online 19 August 2019
Editor: Stephan
Stieberger
Abstract
We
study the effect of non-Abelian T-duality (NATD) on D-brane solutions of type II supergravity.
Knowledge of the full brane solution allows us to track the brane charges and the corresponding brane
configurations, thus providing justification for brane setups previously proposed in the literature and for the
common lore that Dp brane solutions give rise to D(p+1)-D(p+3)-NS5 backgrounds under SU(2) NATD
transverse to the brane. In brane solutions where spacetime is empty and flat at spatial infinity before NATD,
the spatial infinity of the NATD is universal, i.e. independent of the initial brane configuration. Furthermore,
it gives enough information to determine the ranges of all coordinates after NATD. In the more complicated
examples of the D2 branes considered here, where spacetime is not asymptotically flat before NATD, the
interpretation of the dual solutions remains unclear. In the case of supersymmetric D2 branes arising from
M2 reductions to IIA on Sasaki-Einstein seven-manifolds, we explicitly verify that the solution obeys the
appropriate generalized spinor equations for a supersymmetric domain wall in four dimensions. We also
investigate the existence of supersymmetric mass-deformed D2 brane solutions.
© 2019 The Author(s). Published by Elsevier B.V. This is an open access article under the CC BY license
(http://creativecommons.org/licenses/by/4.0/). Funded by SCOAP
3
.
*
Corresponding author.
E-mail
addresses: rterrisse@ipnl.in2p3.fr (R. Terrisse), tsimpis@ipnl.in2p3.fr (D. Tsimpis), cwhiting@bates.edu
(C.A. Whiting).
https://doi.org/10.1016/j.nuclphysb.2019.114733
0550-3213/© 2019
The Author(s). Published by Elsevier B.V. This is an open access article under the CC BY license
(http://creativecommons.org/licenses/by/4.0/). Funded by SCOAP
3
.

2 R. Terrisse et al. / Nuclear Physics B 947 (2019) 114733
1. Introduction
Non-Abelian T-duality (NATD) has recently attracted renewed interest, not least as a tool for
generating new supergravity solutions. A partial list of related literature includes [1–13]. One
problem in this context is that NATD only carries local information: even when the starting
point (the “seed”) is a globally well-defined solution, NA
TD will typically generate a highly
complicated local solution whose global completion, if it exists, is completely obscured. The
main motivation of the present paper is to consider, as seeds of the NATD, full-fledged brane
solutions – as opposed to AdS near-horizon solutions, which has been the case before. The point
is that, as we will see, being able to follo
w the interpolation between the near-horizon and spatial
infinity limit, gives us a better handle on the brane configuration and the global properties of the
dual.
Before NA
TD, standard intersecting brane solutions (i.e. those following the simple harmonic
superposition rule) often interpolate between two asymptotic regions, each of which is an inde-
pendent supergravity solution in its own right: flat space at spatial infinity, and the near-horizon
limit – which in the examples considered here always contains an AdS f
actor. In fact the brane
is not strictly-speaking present in these solutions: the brane backreacts on the flat space in which
it is initially inserted and dissolves into flux, so that the resulting solution is without sources.
1
In
the interpolating and near-horizon solutions there is still a remnant of the brane, whose charge
can be computed by integrating the flux.
The NA
TD of the spatial infinity limit of a standard intersecting brane solution is then univer-
sal, i.e. it is the same for all standard intersecting brane solutions: it is simply the NA TD of flat
space. As we will see in detail in section 2.2.2, in this case an SU(2) NATD generates a distrib
u-
tion, whose density can be determined explicitly, of parallel NS5 branes continuously distributed
along a half line. However after NATD the notion of spatial infinity limit and near-horizon limit
are no longer necessarily meaningful. Still, as previously stated, both limits are genuine solu-
tions so that NA TD will generate ne
w solutions out of them. These will be called respectively
the spatial infinity and near-horizon limit of the dual. For the case of the D3 brane, discussed in
section 2, this definition leads to the commutative diagram of Fig. 1.
Furthermore, all e
xamples considered here will be seen to be consistent with the common
lore that Dp brane solutions give rise to D(p+1)-D(p+3)-NS5 backgrounds under SU(2) NATD
transverse to the brane [14].
2
More generally, for nonstandard brane solutions, such as the D2 branes considered here in
sections 4, 5, 6, the geometry may not asymptote to flat space even before NATD. In that case the
original solution and its dual will in general contain non-vanishing fluxes even at spatial infinity.
Nevertheless, by zooming in near the locus of the NS5, one can still see the presence of a contin-
uous distrib
ution of NS5 branes in accordance with the harmonic superposition prescription for
intersecting branes.
Having the full interpolating solution can f
acilitate reading off the possible global completions
of the geometry after NA TD. In particular the topology of the slices r = constant can be studied
more easily by taking the spatial infinity limit r →∞, where the various expressions simplify.
1
Nevertheless the harmonic superposition rule allows us to trace the original source (i.e. before backreaction) as a
delta function defined in flat space.
2
Some early examples where this has been hinted at through specific examples are in [8,10], but it was proposed
generally in [14].

R. Terrisse et al. / Nuclear Physics B 947 (2019) 114733 3
Fig. 1. (a) D3 brane in flat space; (b) empty flat space; (c) configuration of intersecting D4-D6-NS5 branes;
(d) continuous linear distribution of NS5 branes along a half line. The spatial infinity limit of the dual
solution is defined by taking the limit before the NATD.
As already mentioned, this becomes most clear in the standard cases where, before the NATD,
the space becomes flat at spatial infinity and the NATD is universal.
In order to describe the supersymmetric D2-branes of our paper arising from M2 reductions to
IIA on Sasaki-Einstein se
ven-manifolds, we used the formalism of generalized geometry and the
seven-dimensional pure spinors of [15]. We explicitly verify that this class of solutions obeys the
appropriate generalized spinor equations for a supersymmetric domain wa
ll in four dimensions.
One of our main motivations in deriving these supersymmetric domain wall equations was to
search for the brane solution, if it exists, whose near horizon limit corresponds to the massive
IIA solution found in [16]. The near horizon limit of the D2 brane solution we study in section 4
corresponds to the massless limit and pro
vides a simple solution to these supersymmetry equa-
tions in the case of SU(3) structure. A longer term goal is to understand whether the massive IIA
deformation of the backgrounds in section 4 are related to a class of massive IIA AdS
4
solutions
[17] which arise as a compactification from AdS
7
, and are dual to 3d twisted compactifications
of 6d (1, 0) SCFTs. This work was initiated as a first step towards perhaps a better understanding
of the mass deformation solution in [16] and its NATD found in [13]in that context. While we
were unable to find that interpolating mass deformed solution in this paper
, by investigating the

4 R. Terrisse et al. / Nuclear Physics B 947 (2019) 114733
existence of supersymmetric mass-deformed D2 brane solutions we have ruled out a large class
of Ansätze.
The outline of the paper is as follo
ws. We revisit the case of the D3 brane in section 2. Various
D2 brane solutions are examined in sections 4, 5, 6. These are obtained by reduction from eleven
dimensional solutions of M2 branes transverse to cones over S
7
or Y
p,q
reviewed in section 3.
In section 7 we examine massive deformations of the supersymmetric massless IIA D2 brane
solutions of section 4. We start by casting the supersymmetry equations of the branes in the
formalism of generalized geometry in section 7.1. Massive deformations of the resulting pure
spinor equations are examined in section 7.2. We conclude in section 8. In the appendix we
e
xplain our various conventions and compare them to the literature.
2. D3 brane
The metric describing a stack of parallel D3 branes is given by,
ds
2
=H(r)
−1/2
ds
2
(R
1,3
) +H(r)
1/2
[dr
2
+r
2
ds
2
(S
5
)] , (1)
where H(r) =(1 +
L
4
r
4
). The S
5
is parameterized as follows,
ds
2
(S
5
) =dα
2
+sin
2
αdθ
2
+
1
4
cos
2
α(σ
2
1
+σ
2
2
+σ
2
3
), (2)
where α ∈[0,
π
2
], θ ∈[0, 2π], and σ
i
are left-invariant SU(2) Maurer Cartan one-forms given
by,
σ
1
=−sin ψ
1
dθ
1
+cosψ
1
sin θ
1
dφ
1
σ
2
=cos ψ
1
dθ
1
+sinψ
1
sin θ
1
dφ
1
σ
3
=cos θ
1
dφ
1
+dψ
1
, (3)
with ranges ψ
1
∈[0, 4π ], θ
1
∈[0, π ], φ
1
∈[0, 2π ]. This background is supported by a constant
dilaton and an F
5
flux given by,
F
5
=(1 +)dx
0
∧dx
1
∧dx
2
∧dx
3
∧dH(r)
−1
=dx
0
∧dx
1
∧dx
2
∧dx
3
∧dH(r)
−1
−4L
4
d
5
. (4)
Upon quantization of the five-form flux, one obtains the well-known relation between the con-
stant L in the harmonic function and the number N
D3
of D3 branes: L
4
=4πα
2
N
D3
.
The D3 branes lie along the R
1,3
directions. This can be seen in a probe approach. Consider
the same expression as (4)for a flux living now in R
1,9
. The coordinates now refer to the metric
(1), but with H = 1. Since in spherical coordinates the S
5
collapses at r = 0, its volume form
d
5
is ill-defined. However F
5
is a well-defined current (i.e. a distribution-valued form) and we
can compute:
dF
5
=d F
5
=4L
4
δ(r)dr ∧d
5
(5)
This means that a brane is inserted in r = 0. In this coordinate system this is a codimension 6
space, and thus a D3 lying along R
1,3
. In the transverse space R
6
the brane looks like a point.
The D3 no
w acts as a source for the flux F
5
, which backreacts on the metric through Ein-
stein’s equations to give (1). The global geometry has changed, and the S
5
no longer collapses.
The supergravity equations are solved without sources and the brane cannot be seen anymore.
Nevertheless the information about the brane is still present in the charge carried by the flux.
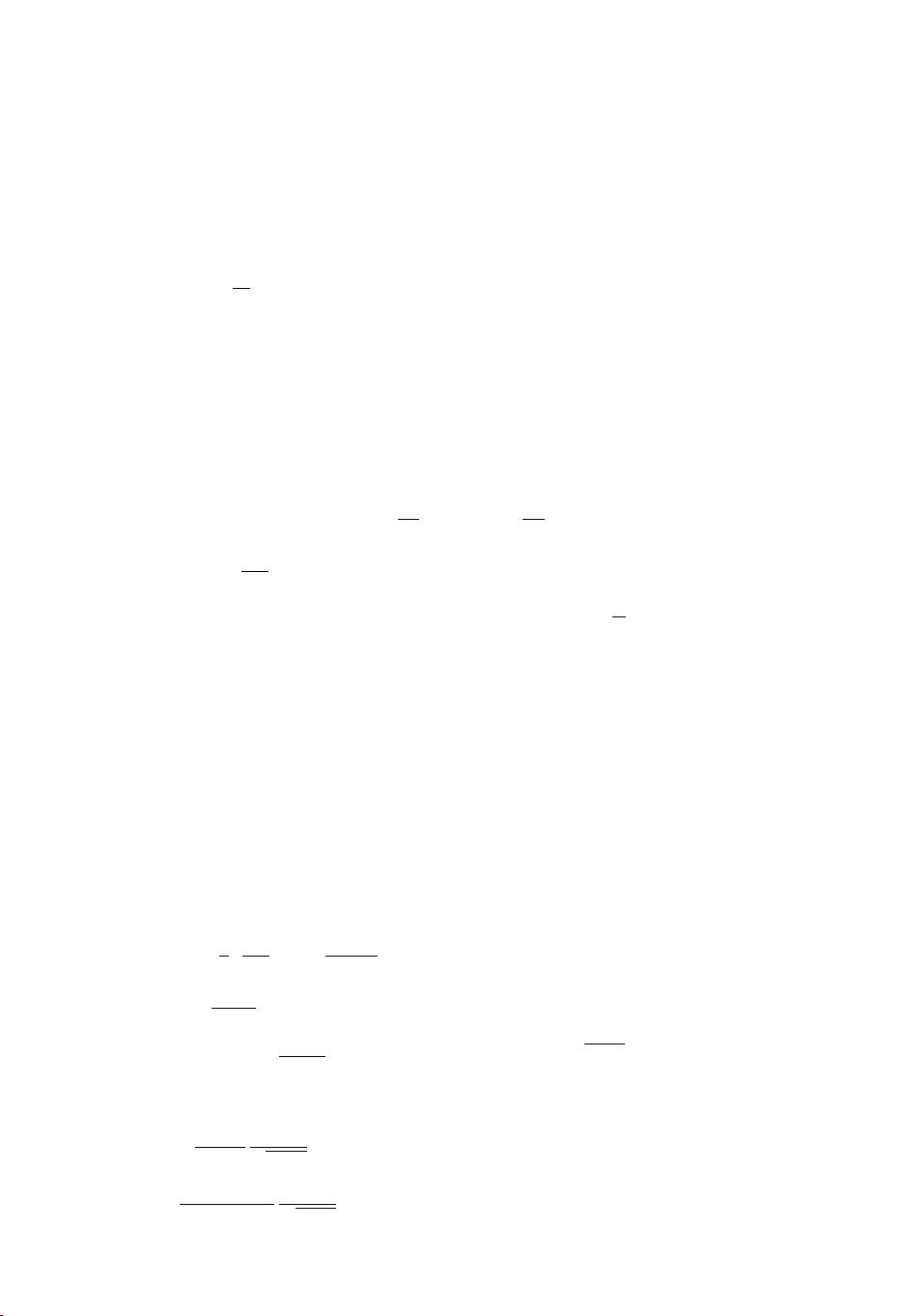
R. Terrisse et al. / Nuclear Physics B 947 (2019) 114733 5
2.1. Near-Horizon and spatial infinity
Taking (1)as an ansatz for the metric, the supergravity equations reduce to an equation on H .
In the probe interpretation this amounts to saying that H is harmonic in the transverse space. If
we further constrain H to depend on r only, the general solution is of the form,
H(r)=a +
b
r
4
, (6)
where a and b are two integration constants. b can readily be interpreted as the brane charge.
Then two limiting cases arise:
Spatial infinity: If b =0, H is a constant and the space is flat without flux: no brane is inserted.
Since H →a when r →∞, this case is called the spatial infinity limit.
Near horizon: If a =0, the solution becomes,
ds
2
=ds
2
(AdS
5
) +L
2
ds
2
(S
5
) =
r
2
L
2
ds
2
(R
1,3
) +
L
2
r
2
dr
2
+L
2
ds
2
(S
5
)
F
5
=(1 +)
4r
3
L
4
dx
0
∧dx
1
∧dx
2
∧dx
3
∧dr, (7)
which is the well-known AdS
5
×S
5
background. For r → 0, H ∼
b
r
4
so that this case is called
the near horizon limit.
It is remarkable at first sight that both limits correspond to genuine backgrounds. The reason
behind this is that they ultimately correspond to different choices of integration constants. These
considerations might seem trivial for now, but they will be relevant in the following, when the
brane configurations become more involved.
2.2. The NATD
After performing NATD along the SU(2) isometry in the σ
i
, cf. (3), the background (1), (4)
becomes,
ds
2
=H(r)
−1/2
ds
2
(R
1,3
) +H(r)
1/2
[dr
2
+r
2
(dα
2
+sin
2
αdθ
2
)]
+
1
4
α
2
dρ
2
+
2
64α
ρ
2
(dχ
2
+sin
2
χdξ
2
)
B
2
=−
ρ
3
256
sin χdχ ∧dξ
e
−2φ
=, =
64α
3
(α
2
ρ
2
+
2
), =r
2
cos
2
α
H(r) , (8)
and nonzero RR fluxes given by,
F
2
=−
8α
3/2
H
(r)
√
H(r)
r
3
cosα sin αdα ∧dθ
F
4
=
2
2048α
3/2
H
(r)
√
H(r)
r
3
ρ
3
cosα sin α sinχdα ∧dθ ∧dχ ∧dξ . (9)
剩余38页未读,继续阅读
资源评论

weixin_38645266
- 粉丝: 4
- 资源: 948
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 毕设和企业适用springboot商城类及智慧园区智能化管理系统源码+论文+视频.zip
- 毕设和企业适用springboot人才招聘类及网络营销平台源码+论文+视频.zip
- 毕设和企业适用springboot人才招聘类及视频直播系统源码+论文+视频.zip
- 毕设和企业适用springboot人才招聘类及无人机管理平台源码+论文+视频.zip
- 毕设和企业适用springboot汽车电商类及新闻传播平台源码+论文+视频.zip
- 毕设和企业适用springboot汽车电商类及行业资讯平台源码+论文+视频.zip
- 毕设和企业适用springboot汽车电商类及医疗信息管理平台源码+论文+视频.zip
- 毕设和企业适用springboot人才招聘类及在线教育互动平台源码+论文+视频.zip
- 毕设和企业适用springboot人才招聘类及云端协作平台源码+论文+视频.zip
- 毕设和企业适用springboot人才招聘类及在线药品管理平台源码+论文+视频.zip
- 毕设和企业适用springboot汽车电商类及语音识别系统源码+论文+视频.zip
- 毕设和企业适用springboot汽车电商类及云端储物管理系统源码+论文+视频.zip
- 毕设和企业适用springboot汽车电商类及在线学习平台源码+论文+视频.zip
- 毕设和企业适用springboot人才招聘类及智慧医疗管理平台源码+论文+视频.zip
- 毕设和企业适用springboot人才招聘类及智能农业解决方案源码+论文+视频.zip
- 毕设和企业适用springboot人才招聘类及智能农业平台源码+论文+视频.zip
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功