Numericalstudyforthecalculationofcomputer-generatedhologramincolorholographic3Dprojectionenabledbymodifiedwavefrontrecordingplanemethod资源-CSDN文库

176 浏览量 2021-02-21 20:31:17 上传评论收藏 1.3MB PDF 举报

Numerical study for the calculation of computer-generated hologram in color holographic 3D projection enabled by modified wavefront recording plane method 本研究介绍了一种用于彩色全息3D投影的计算机生成全息图(CGH)计算方法，该方法基于改进的波前记录平面(WRP)方法。文中首先回顾了全息投影技术，特别是计算机生成全息图在全息显示领域的应用，以及该领域面临的挑战。彩色全息投影因其能够提供高亮度、高对比度和宽色域的图像而受到关注，被认为是实现无需任何可穿戴设备的真三维显示的最有潜力的技术。然而，三维物体的巨大信息量导致了在生成用于投影三维物体的CGH时的长时间计算。为了解决这一问题，本文提出了一种计算方法，它将彩色3D物体分解为红、绿、蓝三个颜色分量。针对每个颜色分量，建立了根据3D物体的深度图非均匀采样的虚拟波前记录平面(WRP)。然后，采用移动菲涅尔衍射算法从非均匀采样的WRP计算出每个颜色分量的全息图。基于多路复用编码方法，将RGB分量的三个全息图编码到一个单一的CGH中。该方法将CGH生成中的衍射计算从巨大的三维体素转换为三个二维平面图像，从而减少了计算成本。在实验结果中，采用所提出的方法生成的CGH能够投影出清晰质量的可缩放彩色3D物体。研究内容涵盖了全息投影的基本原理、彩色全息技术的发展现状、全息显示的关键技术点以及研究中所采用的改进波前记录平面方法和移动菲涅尔衍射算法的细节。此外，文中还讨论了全息图的编码技术以及多路复用编码方法在减少计算量方面的优势。本研究的数值实验结果证明了所提方法的有效性，并展示了全息图在高质量彩色全息显示中的潜力。研究结果对于全息投影、计算机全息学以及信息显示与可视化领域具有重要的参考价值和应用前景。研究的关键词包括颜色全息学、全息显示、计算机全息学以及衍射等。在具体实现方面，研究中所涉及的技术点和算法应用，包括非均匀采样、移动菲涅尔衍射算法以及多路复用编码方法，为全息技术的进一步研究和发展提供了理论基础和技术支持。

资源推荐

资源详情

资源评论

Contents lists available at ScienceDirect

Optics Communications

journal homepage: www.elsevier.com/locate/optcom

Numerical study for the calculation of computer-generated hologram in

color holographic 3D projection enabled by modiﬁed wavefront recording

plane method

Chenliang Chang

, Yijun Qi

, Jun Wu

, Caojin Yuan

, Shouping Nie

⁎

, Jun Xia

⁎

Jiangsu Key Laboratory for Opto-Electronic Technology, School of Physics and Technology, Nanjing Normal University, WenYuan Road 1, 210023

Nanjing, China

Joint International Research Laboratory of Information Display and Visualization, School of Electronic Science and Engineering, Southeast University, Si

Pai Lou 2, 210096 Nanjing, China

ARTICLE INFO

Keywords:

Color holography

Holographic display

Computer holography

Diﬀraction

ABSTRACT

A method of calculating computer-generated hologram (CGH) for color holographic 3D projection is proposed.

A color 3D object is decomposed into red, green and blue components. For each color component, a virtual

wavefront recording plane (WRP) is established which is nonuniformly sampled according to the depth map of

the 3D object. The hologram of each color component is calculated from the nonuniform sampled WRP using

the shifted Fresnel diﬀraction algorithm. Finally three holograms of RGB components are encoded into one

single CGH based on the multiplexing encoding method. The computational cost of CGH generation is reduced

by converting diﬀraction calculation from huge 3D voxels to three 2D planar images. Numerical experimental

results show that the CGH generated by our method is capable to project zoomable color 3D object with clear

quality.

1. Introduction

Laser based holographic projection from a computer-generated

hologram (CGH) can provide high brightness, high contrast and wide

color gamut images. Moreover, since holographic technique has

potential for reconstructing all the three-dimensional (3D) information

of an object in space, holographic projection is also considered to be the

most potential technique to achieve true 3D display without any

wearable devices. However, the huge amount of three dimensional

information results in long calculation time in CGH generation for

projection 3D object. Many methods have been proposed in order to

accelerate the calculation of CGH. For example, the point based

method with look-up tables is an eﬀective method in which the

wavefront of point light source is pre-calculated and saved in a look-

up table (LUT) [1–3], however, it requires large memories for the

storage of LUT. Other popular methods include the layer-based

methods [4–6] and the polygon-based methods [7–9]. In these

methods, the basic idea is to model the 3D object into numerous 2D

planes, either parallel planes or tilted planes, and the calculation of

CGH can be converted from 3D information to 2D planes in which the

fast Fourier transform (FFT) algorithm could be employed for further

accelerating. Nevertheless, the total calculation time of CGH is

proportional to the numbers of the modeled planes. While this number

is always large (sometimes more than ten thousands planes) in order to

accurate sample a 3D object, these methods are still remains cumber-

some. Recently, a simple method of CGH calculation based on the

nonuniform sampled wavefront recording plane (WRP) method is

proposed [10], which is derived from the well-known WRP methods

invented by Shimobaba [11,12]. This method allows calculating CGH

only from 2D intensity map of a 3D object by establishing a virtual

plane close to the object, therefore the calculation can be accelerated by

using the nonuniform fast Fourier transform (NUFFT) algorithm.

Another important ﬁeld of holographic projection is color projec-

tion. Holographic color projection can generally be realized by: time

division [13,14], depth division [15,16] and space division [17,18].In

time division method, three sub-holograms of red, green and blue

component of color object are calculated and displayed on the SLM in

sequence, in which we need to control each laser source and sub-

hologram synchronously. In addition, this method requires very high

frame rate devices to display sub-holograms for the eﬀect to be seen by

a human eye. Another kind of method use only one SLM to achieve

color projection, Makowski proposed a method by dividing one SLM

into three regions with each region loaded one component hologram

[17], but the resolution is lost by taking advantage of only one third of

http://dx.doi.org/10.1016/j.optcom.2016.10.073

Received 5 October 2016; Received in revised form 22 October 2016; Accepted 26 October 2016

⁎

Corresponding authors.

E-mail addresses: nieshouping@njnu.edu.cn (S. Nie), xiajun@seu.edu.cn (J. Xia).

Optics Communications 387 (2017) 267–274

Available online 01 December 2016

MARK

the whole SLM for one color component. More eﬀective method is to

use multiplexing by encoding three color components into one SLM

with whole area [18]. However, most of these methods only consider

the projection of two dimensional color images. For dynamic holo-

graphic 3D projection, Gaolei Xue proposed a method to reconstruct

full color 3D object by modeling its complex amplitude [19]. In this

method, the CGH of each color component is calculated using polygon-

based methods and three CGHs are synthesized into one CGH by

multiplexing encoding method. However, the calculation time of the

CGH will be proportional to the numbers of the modeled polygons.

In this paper we propose a method to simply calculate CGH for

color holographic 3D projection, based on the combination of the

nonuniform sampled WRP method and the multiplexing encoding

technique. The CGH calculation is simple and fast, the calculation time

is independent on the number of object points. The CGH is capable to

reconstruct zoomable color 3D object in holographic projection system.

2. Method of CGH generation in color holographic 3D

projection

2.1. CGH calculation from 3D object using nonuniform sampled WRP

The nonuniform sampled WRP (NS-WRP) based method [10]

presents the eﬀectiveness to simply and fast calculate a CGH that can

project 3D object with perceptive depth and zoomable function. The

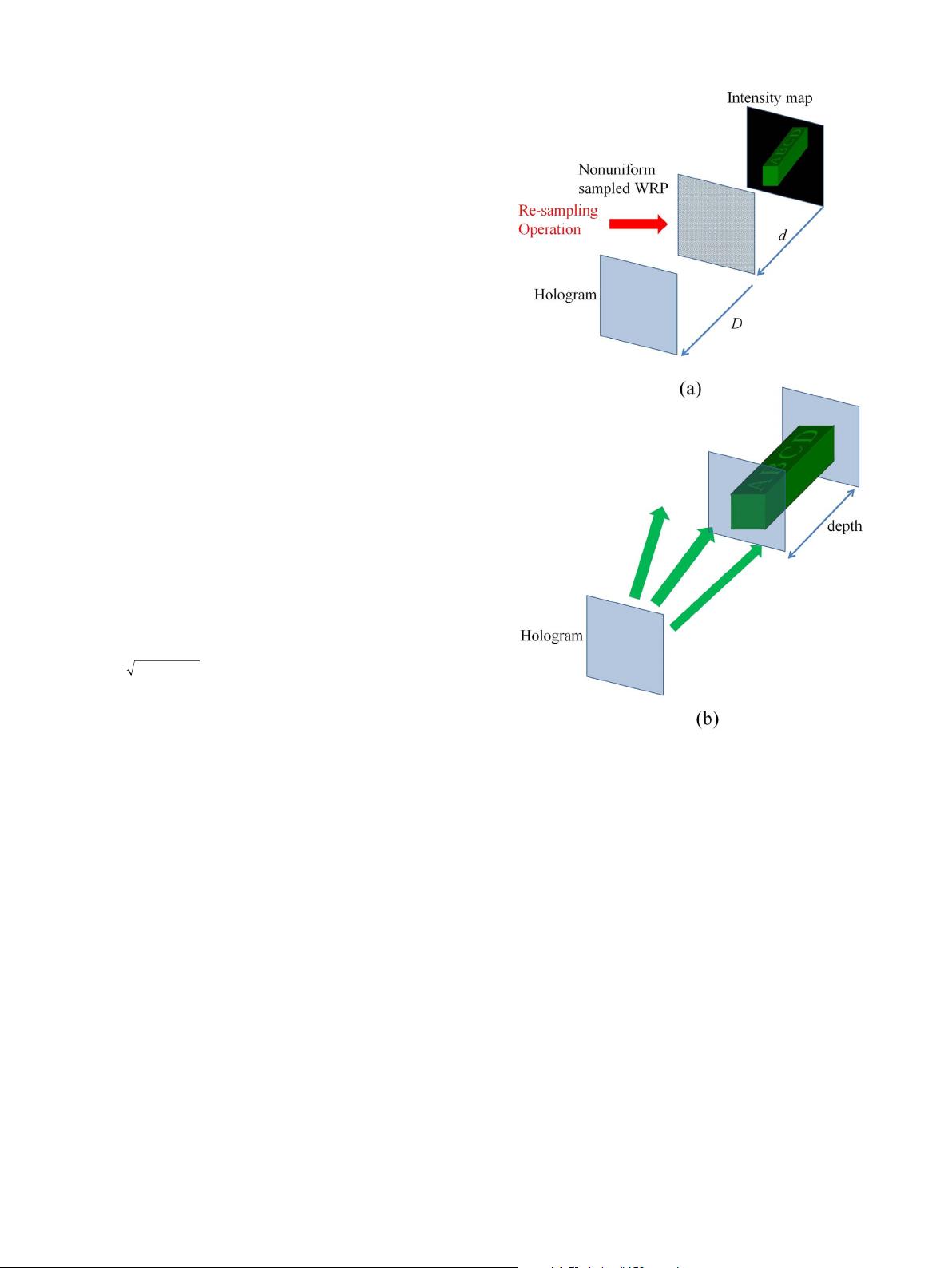
schematic diagram of this method of calculating CGH from a mono-

chrome 3D object is shown in Fig. 1(a). First, a virtual wavefront

recording plane (WRP) which is suﬃciently close to the 3D object is

established. The 3D object is represented by a 2D intensity map I(u, v)

and a depth map d(u, v). The intensity map I(u, v) is located at distance

min

from the WRP where d

min

is the minimum value of d(u, v). Both of

the intensity map and the WRP is sampled in the same way and their

sampling pitch is given according to the depth map as:

Wuv d duv du(, )= / (, )⋅

min

(1)

Where du is the transversal pixel pitch of the 3D object. In this way,

the diﬀerent depth value d(u, v) of each object point give rise to the

nonuniform sampled (NS) WRP and the intensity map. Next, the

calculation of the NS-WRP from the NS intensity map is performed by

using the nonuniform fast Fourier transform (NUFFT) based angular

spectrum method expressed as:

xw yw NUFFT NUFFT I u v T f f( , ) = 2{ 1[ ( , )]⋅ ( , )}

(2)

Where W(xw, yw) is the light ﬁeld of the WRP and T(f

, f

) is the

transfer function of the angular spectrum method. NUFFT1 and

NUFFT2 denote the ﬁrst and second type of the NUFFT respectively.

The detailed explanation of NUFFT can be found in Ref. [20–22]. After

that the calculated WRP W(xw, yw) is forcely re-sampled to an

uniform sampled WRP W(xw’, yw’) with the samping pitch of du. In

the last step of the method, the hologram is obtained by calculating the

diﬀraction from the W(xw’ , yw’) employing the ARSS –Fresnel

diﬀraction algorithm [23]. The calculation of the hologram H(x, y)is

given by:

x y FFT FFT W xw yw iφ FFT iφ ct( , ) = { [ ( , )⋅exp( )]⋅ [exp( )⋅Re ]}

−1

(3)

Where f

and f

are the quadratic phase term and Rect is a rectangular

function that reduces aliasing noise. Their detailed expression can be

found in Ref. [23].

Fig. 1(b) shows the reconstruction of the hologram calculated by the

above described NS-WRP based method. Due to the resampling

operation from nonuniform sampled WRP to uniform sampled WRP

in the calculation step, each object point of the intensity map will be

reconstructed to a new position at its original depth distance according

to the relations between the reconstruction distance and the sampling

pitch change [10]. Consequently the whole monochrome 3D object

with inherent depth cue can be reconstructed.

2.2. CGH synthesize from color 3D object by multiplexing technique

The calculation process of the CGH from a color 3D object is shown

in Fig. 2. The color 3D object can be divided into RGB component.

Each divided component is represented by a 2D intensity map and

distributed transversely in space as shown in Fig. 2. Then the intensity

map of each color component is propagated toward to the three NS-

WRPs directly and separately, using the NUFFT based angular

spectrum method. After resampling three NS-WRPs to nonuniform

sampled WRPs according to the depth map of the object, we calculate

the sub-hologram of RGB component from each re-sampled WRP.

Here the propagation from each WRP to the hologram is oﬀ-axis

diﬀraction, hence we employ the ARSS- Fresnel diﬀraction algorithm

[23] to calculate the oﬀ-axis diﬀraction and generate three complex

sub-holograms of RGB component. Finally we superimpose the three

complex sub-holograms of RGB component in order to synthesize one

ﬁnal CGH.

The reconstruction process of the CGH is shown in Fig. 3. In the

reconstruction, the CGH is illuminated simultaneously by three

reference lights of RGB colors with diﬀerent angles. By properly

adjusting the angle θ of the three illumination lights, the RGB

component of the target object can be reconstructed at the desired

Fig. 1. (a) Hologram calculation by the NS-WRP based method. (b) Reconstruction of

the hologram..

C. Chang et al.

Optics Communications 387 (2017) 267–274

268

剩余7页未读，继续阅读

评论收藏

内容反馈

weixin_38640168

粉丝: 6
资源: 959

Numerical study for the calculation of computer-generated hologr...

最新资源

Numerical study for the calculation of computer-generated hologr...

Numerical Methods for the Solution of Ill-Posed Problems

numerical-methods-for-partial-differential-equations.pdf

An mixed analytical-numerical modeling for plate under hot rolling---Part Ⅰ: Temperature model

Fast numerical generation and hybrid encryption of a computer-generated Fresnel holographic video sequence

Numerical-Methods-for-Structured-Markov-Chains

Numerical study of Kibble-Zurek Mechanism in the presence of long-range interaction

Numerical Techniques in Electromagnetics

numerical-geometry-of-non-rigid-shapes.pdf

Acceleration method for computer generated spherical hologram calculation of real objects using graphics processing unit (Invited Paper)

Numerical Study of Wetting Transitions Using Cahn-Hillard model

Numerical Recipes - The Art of Scientific Computing(3rd)【数值分析方法库

D.E.Knuth(高德纳)著，计算机程序设计艺术第二卷,英文原版，epub

A Numerical Study of the High-Velocity Impact Response

Numerical Methods for Engineers-McGraw-Hill(2014)

ＣＦＤ经典著作：numerical partial differential equation - finite difference method

【船级社】 KR Guidelines on Numerical Calculations for the purpose of

Experimental and Numerical Study on the Characteristics of Liquid Phase LPG and Diesel Fuel Sprays

Resource Optimization and Security for Cloud Services(Wiley,2014)

Numerical Methods for StochasticComputations-A Spectral Method Approach

Numerical Calculation of the Impact of Offshore Wind Power Stations on Hydrodynamic Conditions

一类传染病年龄模型的非标准数值格式_A non-standard numerical scheme for an age-of-

Numerical Geometry of Non-Rigid Shapes

Numerical Liner Algebra with Applications

最新资源