《线段的垂直平分线》PPT课件6

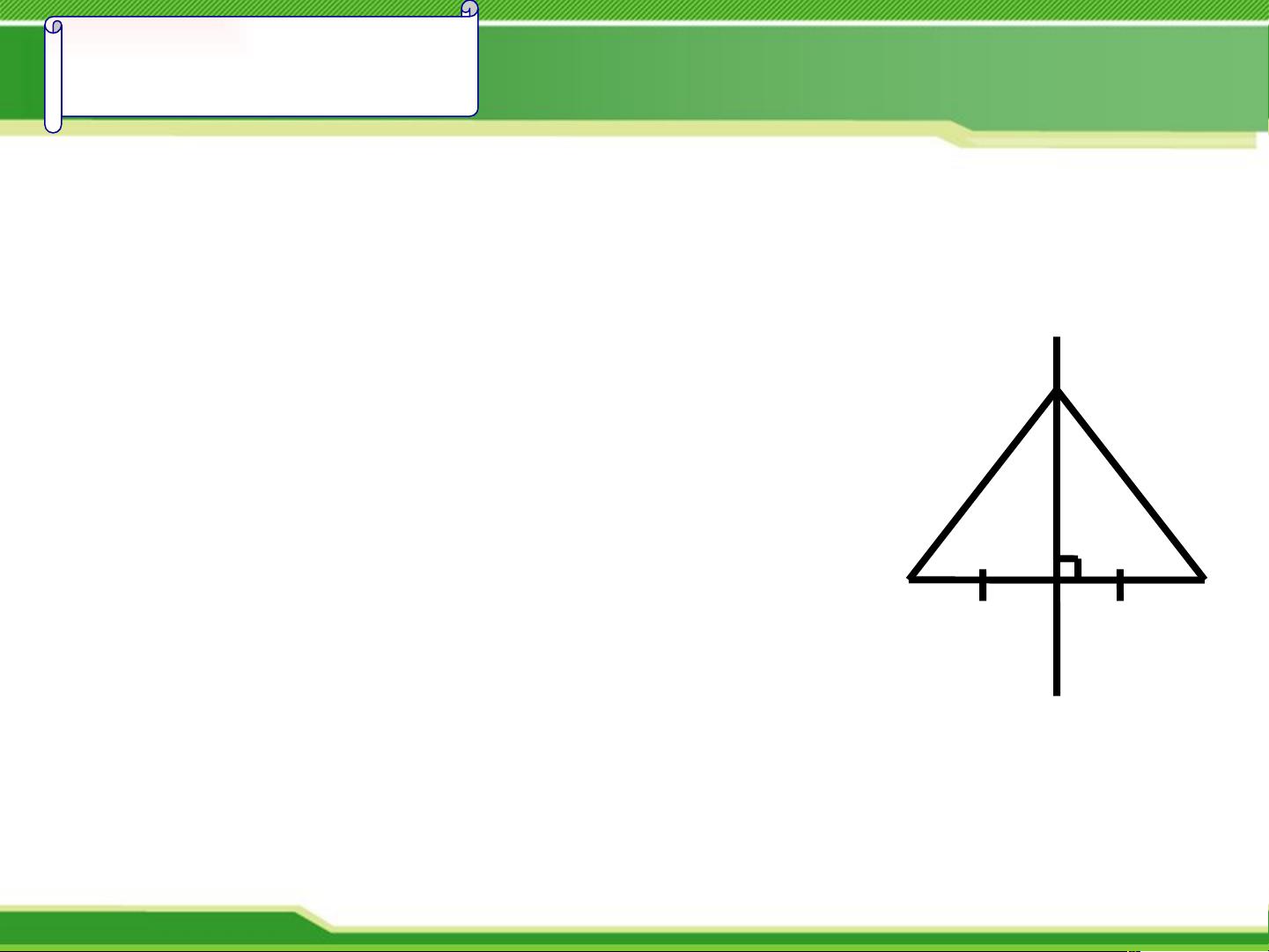
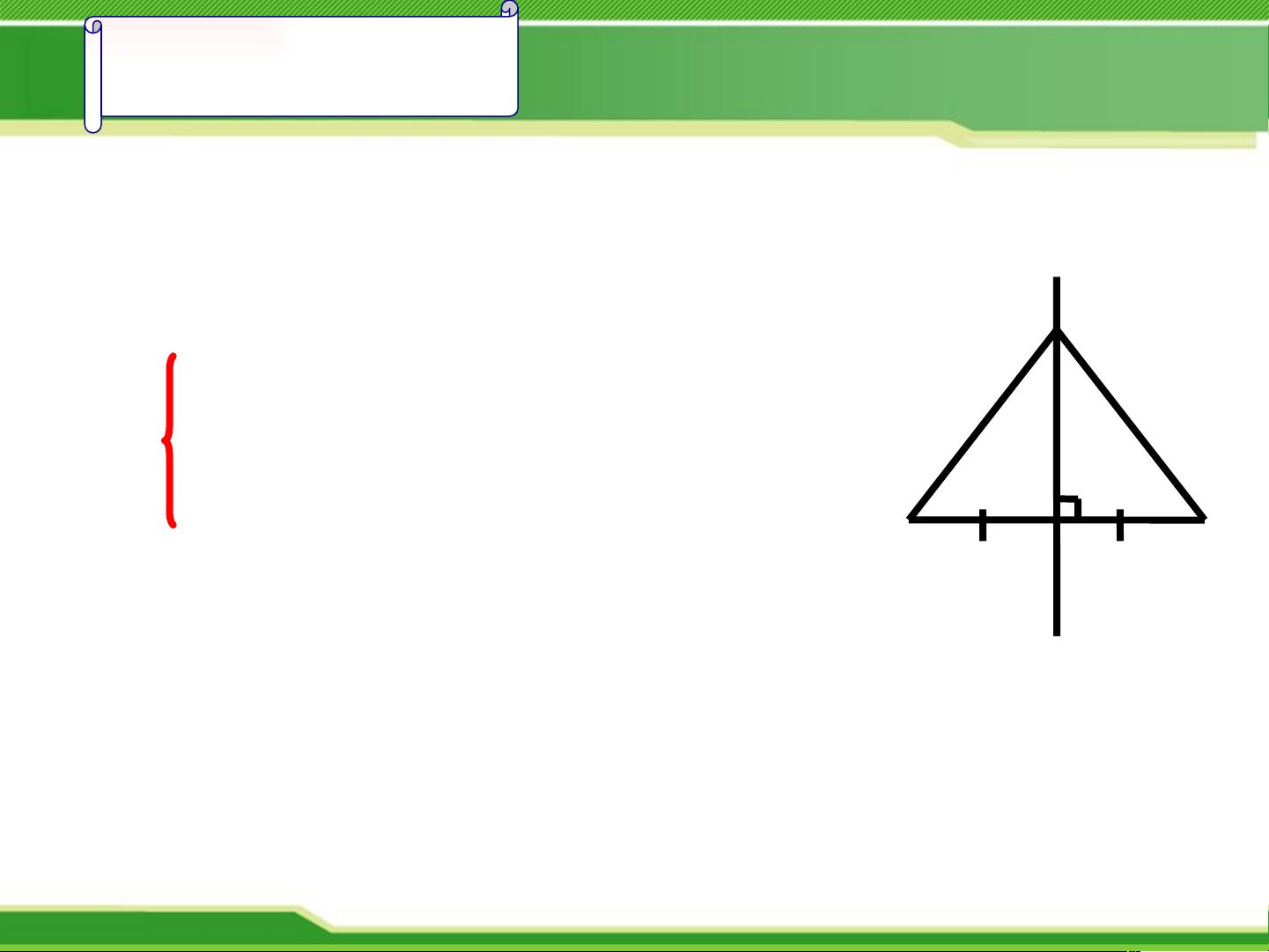
这是整理发布的一款《线段的垂直平分线》课件PPT，PPT主要以初中数学课程为主，适合老师及学生...该文档为《线段的垂直平分线》PPT课件6，是一份很不错的参考资料，具有较高参考价值，感兴趣的可以下载看看 【线段的垂直平分线】是几何学中的一个核心概念，主要出现在初中的数学课程中，对于理解和解决几何问题有着至关重要的作用。线段的垂直平分线是一条通过线段中点并且与线段垂直的直线。这条直线的一个显著特性是，它上面的任何一点到线段两端点的距离都是相等的。 这个特性可以通过严格的几何证明来建立。例如，假设我们有线段AB，其垂直平分线MN，点P位于MN上。如果能够证明PA=PB，那么就可以确认点P在AB的垂直平分线上。证明通常使用全等三角形的方法进行。在证明过程中，首先可以指出MN垂直于AB，这意味着∠PCA和∠PCB都是直角。接着，由于AC=BC（线段的对称性），加上∠PCA=∠PCB（因为它们都是直角）和公共边PC，我们可以应用边边边（SAS）原则，证明三角形PCA和PCB全等。全等三角形的对应边相等，所以PA=PB，这就证实了点P在AB的垂直平分线上。 这个性质不仅有助于证明线段相等，还可以用来证明点的位置，比如判断点是否在线段的垂直平分线上。在实际应用中，它常用于解决几何作图问题，如构造等腰三角形或者找到线段中点等。此外，它在平面几何的其他定理证明中也发挥着重要作用，例如三角形的内心、外心等概念的理解和证明。 在基础闯关部分，我们看到了几个例题，如若EC=7cm，由线段的垂直平分线性质可知，ED也将等于7cm，因为E点同时在线段CD的垂直平分线上。同样，如果∠ECD=60°，根据等腰三角形的性质，∠EDC也将是60°。另一道题目中，AC=27，AB的垂直平分线交AC于E，若△BCE的周长为50，则可以通过周长关系求出BC的长度。 这个课件对于学习者来说是一个宝贵的参考资料，提供了丰富的例题和证明方法，有助于巩固对线段垂直平分线概念的理解，提升解决几何问题的能力。同时，提供的网站资源也为学习者提供了更多的学习材料和教程，帮助他们深入理解和掌握相关知识。