
Scale-Space Behavior
of Planar-Curve Corners
Baojiang Zhong,
Kai-Kuang Ma, Senior Member, IEEE,and
Wenhe Liao
Abstract—The curvature scale-space (CSS) technique is suitable for extracting
curvature features from objects with noisy boundaries. To detect corner points in a
multiscale framework, Rattarangsi and Chin investigated the scale-space behavior
of planar-curve corners. Unfortunately, their investigation was based on an
incorrect assumption, viz., that planar curves have no shrinkage under evolution.
In the present paper, this mistake is corrected. First, it is demonstrated that a
planar curve may shrink nonuniformly as it evolves across increasing scales.
Then, by taking into account the shrinkage effect of evolved curves, the CSS
trajectory maps of various corner models are investigated and their properties are
summarized. The scale-space trajectory of a corner may either persist, vanish,
merge with a neighboring trajectory, or split into several trajectories. The scale-
space trajectories of adjacent corners may attract each other when the corners
have the same concavity, or repel each other when the corners have opposite
concavities. Finally, we present a standard curvature measure for computing the
CSS maps of digital curves, with which it is shown that planar-curve corners have
consistent scale-space behavior in the digital case as in the continuous case.
Index Terms—Scale space, corner detection, curve evolution, CSS, digital
curves, curvature, discrete curvature, shrinkage rate, evolution trajectory, dual
trajectory.
Ç
1INTRODUCTION
THE curvature scale-space (CSS) technique was de veloped by
Mokhtarian and Mackworth [1] for two-dimensional (2D) shape
representation and analysis. It is based on the classical curve
evolution scheme, which can be mathematically expressed as
x
ðsÞ¼ðx g
ÞðsÞ; y
ðsÞ¼ðy g
ÞðsÞ; ð1Þ
where CðsÞ¼fxðsÞ;yðsÞg represents a planar curve, g
ðsÞ is a
zero-mean Gaussian function with the standard deviation ,
which is treated as a scale parameter for the evolution operation
according to (1). The evolved curve at the scale is denoted by
C
ðsÞ¼fx
ðsÞ;y
ðsÞg to differentiate it from the original curve
CðsÞ¼fxðsÞ;yðsÞg. By evaluating the curvature of points s along
the curve at various scales , a CSS trajectory map can be
generated, either based on the inflection points [1] or based on the
corner points [2] (used in this paper).
Over the past few decades, the CSS technique has been applied
extensively for solving various problems in the field of computer
vision and image processing, such as feature extraction, curve
matching, and object recognition [2], [3], [4], [5], [6], [7], [8], [9]. It
has also been selected as a shape descriptor for image indexing and
retrieval application in the MPEG-7 standard [10].
The CSS technique has demonstrated its successful application
on planar-curve corner detection [2], [6], especially for those object
shapes inherited with fractal-like features and noisy boundaries. In
the area of multiscale corner detection (e.g., [2], [11], [12], [13], [14],
[15], [16], [17]), Rattarangsi and Chin’s work [2] is a representative
contribution. In particular, they investigated the scale-space
behavior of various corner models and summarized a number of
model properties, with which they developed an algorithm for
conducting corner detection in the multiscale framework.
Unfortunately, Rattarangsi and Chin’s investigation on the
scale-space behavior of planar-curve corners was based on an
incorrect assumption, viz., that planar curves have no shrinkage as
they evolve according to (1). As a result, the parameter s is treated
as the arc-length parameter both of the original curve CðsÞ and of
the evolved curve C
ðsÞ. The curvature of C
ðsÞ, denoted as
ðsÞ,
was therefore computed in [2] by
ðsÞ¼
_
x
ðsÞ
€
y
ðsÞ
€
x
ðsÞ
_
y
ðsÞ; ð2Þ
where the symbol “” denotes the derivative of the mentioned
variable with respect to s. However, according to a standard
curvature expression [18],
ðsÞ should be computed by
ðsÞ¼
_
x
ðsÞ
€
y
ðsÞ
€
x
ðsÞ
_
y
ðsÞ
ð
_
x
ðsÞ
2
þ
_
y
ðsÞ
2
Þ
3=2
: ð3Þ
By a comparison with (3), it can be seen that (2) holds only if the
arc length of the curve incurs no change throughout the evolution.
However, this is not true! In fact, except a straight line, the arc
length of a planar curve will be reduced, when the curve evolves
with increasing scales.
Let us consider an infinitesimal curve segment containing a
point at s, its arc length (without evolution) is ds ¼ðdxðsÞ
2
þ
dyðsÞ
2
Þ
1=2
. With a curve evolution at the scale , the arc length
becomes ds
¼ðdx
ðsÞ
2
þ dy
ðsÞ
2
Þ
1=2
. The ratio of these two arc-
length measurements, ds
versus ds, is coined as the shrinkage rate
of the evolved curve (at the scale ) in this paper, that is,
r
ðsÞ
ds
ds
¼ð
_
x
ðsÞ
2
þ
_
y
ðsÞ
2
Þ
1=2
: ð4Þ
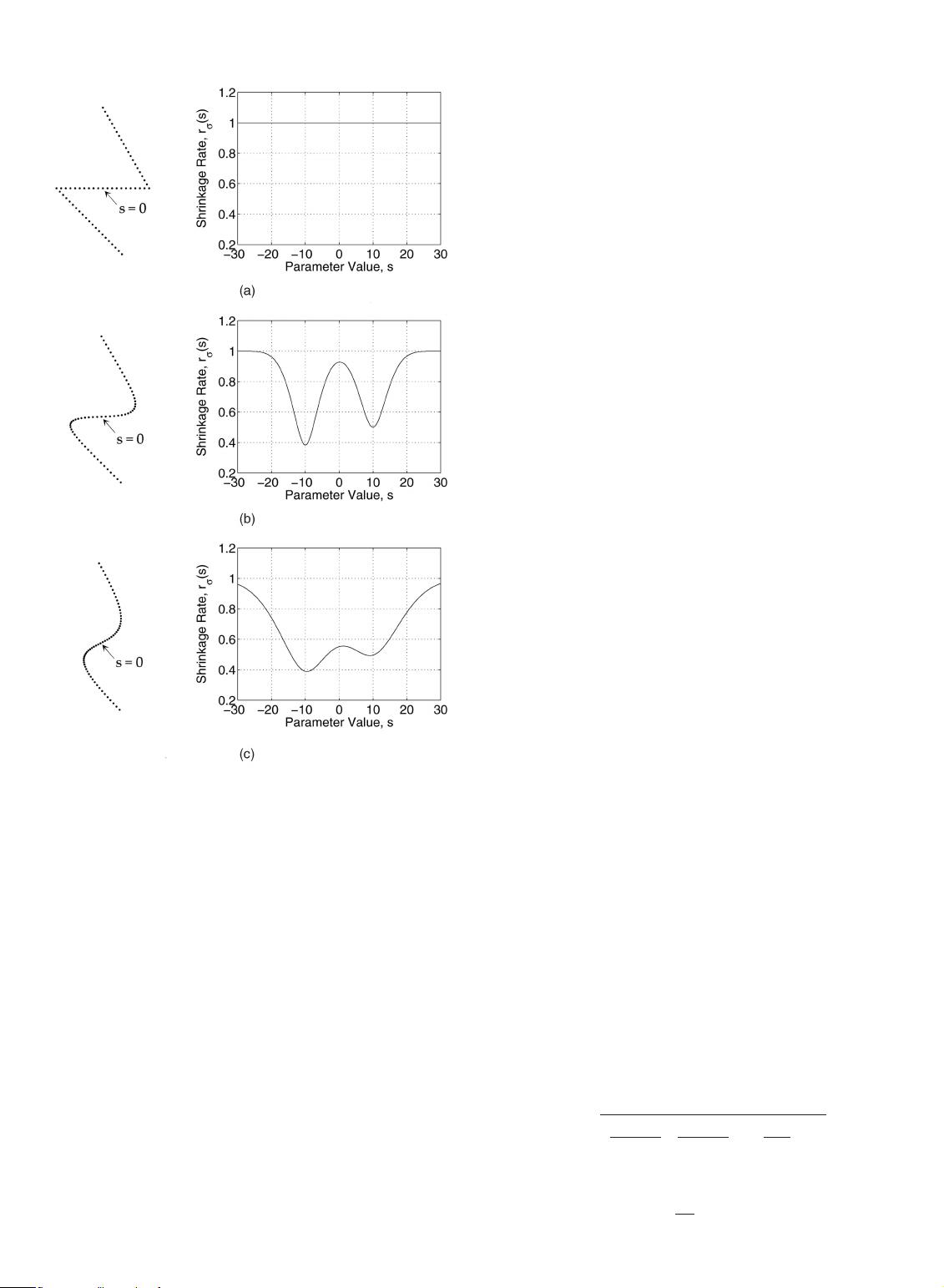
For example, in Fig. 1, the left column illustrates two evolution
cases (i.e., at the scales of ¼ 5 and ¼ 10) of a planar curve and
the right column demonstrates their respective shrinkage rate
r
ðsÞ, from which one can observe that the curve shrinks
nonuniformly across s since r
ðsÞ is not constantly equal to 1 for
all s, when >0. However, (2) and (3), are equivalent to each other
only when r
ðsÞ¼1, for all s. Therefore, it is the curvature
expression (3) that should be used for computing the curvature
ðsÞ, rather than (2).
While the scale-space behavior of corners was investigated for
continuous curves, the CSS corner detection was, in practice,
implemented through digital curves [2]. Note that, in the digital
case, the curvature of evolved planar curves was properly
computed in [2] and, therefore, the shrinkage effect was included
in the implementation of the CSS corner detection. The purpose of
this paper is to correct Rattarangsi and Chin’s mistake made in the
continuous case.
It is worthwhile to point out that, conceptually, the CSS is very
close to the linear Gaussian scale space, of which the foundations
are well established, and the applications cover the whole area of
digital imaging [19], [20], [21], [22], [23], [24], [25], [26], [27], [28],
[29], [30]. In particular, Blom [20] investigated the scale-space
behavior of corners in the 2D monochrome image, while Zhong
and Liao [17] established a direct curvature scale-space theory for
IEEE TRANSACTIONS ON PATTERN ANALYSIS AND MACHINE INTELLIGENCE, VOL. 31, NO. 8, AUGUST 2009 1517
. B. Zhong is with the Department of Mathematics, Nanjing University of
Aeronautics and Astronautics, Nanjing 210016, P.R. China.
E-mail: zhbj@nuaa.edu.cn.
. K.-K. Ma is with the School of Electrical and Electronic Engineering,
Nanyang Technological University, Block S2, Nanyang Avenue, 639798
Singapore, Singapore. E-mail: ekkma@ntu.edu.sg.
. W. Liao is with the College of Mechanical and Electrical Engineering,
Nanjing University of Aeronautics and Astronautics, Nanjing 210016,
China. E-mail: njwho@nuaa.edu.cn.
Manuscript received 4 June, 2008; revised 29 Oct. 2008; accepted 10 Nov.
2008; published online 4 Dec. 2008.
Recommended for acceptance by K. Siddiqi.
For information on obtaining reprints of this article, please send e-mail to:
tpami@computer.org, and reference IEEECS Log Number
TPAMI-2008-06-0330.
Digital Object Identifier no. 10.1109/TPAMI.2008.295.
0162-8828/09/$25.00 ß 2009 IEEE Published by the IEEE Computer Society


 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜 信息提交成功
信息提交成功

