纠缠楔形重建和纠缠纯化资源-CSDN文库

Open

Access

72 浏览量 2020-04-29 02:51:49 上传评论收藏 1.24MB PDF 举报

资源推荐

资源详情

资源评论

Eur. Phys. J. C (2018) 78:646

https://doi.org/10.1140/epjc/s10052-018-6140-2

Regular Article - Theoretical Physics

Entanglement wedge reconstruction and entanglement of

puriﬁcation

Ricardo Espíndola

1,a

, Alberto Güijosa

1,b

, Juan F. Pedraza

2,c

Departamento de Física de Altas Energías, Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México, Apartado Postal 70-543,

04510 Mexico, CDMX, Mexico

Institute for Theoretical Physics, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands

Received: 9 July 2018 / Accepted: 3 August 2018

Abstract In the holographic correspondence, subregion

duality posits that knowledge of the mixed state of a ﬁnite

spacelike region of the boundary theory allows full recon-

struction of a speciﬁc region of the bulk, known as the entan-

glement wedge. This statement has been proven for local bulk

operators. In this paper, specializing ﬁrst for simplicity to a

Rindler wedge of AdS

, we ﬁnd that generic curves within

the wedge are in fact not fully reconstructible with entan-

glement entropies in the corresponding boundary region,

even after using the most general variant of hole-ography,

which was recently shown to sufﬁce for reconstruction of

arbitrary spacelike curves in the Poincaré patch. This lim-

itation is an analog of the familiar phenomenon of entan-

glement shadows, which we call ‘entanglement shade’. We

overcome it by showing that the information about the non-

reconstructible curve segments is encoded in a slight gen-

eralization of the concept of entanglement of puriﬁcation,

whose holographic dual has been discussed very recently.

We introduce the notion of ‘differential puriﬁcation’, and

demonstrate that, in combination with differential entropy, it

enables the complete reconstruction of all spacelike curves

within an arbitrary entanglement wedge in any 3-dimensional

bulk geometry.

Contents

1 Introduction and conclusions ..............

2 Rindler geodesics ....................

2.1 Geodesics at constant time ............

2.2 Time-dependent geodesics contained within the

Rindler wedge ...................

e-mail: ricardo.espindola@correo.nucleares.unam.mx

e-mail: alberto@nucleares.unam.mx

e-mail: jpedraza@uva.nl

3 Criteria for reconstructibility of curves ........

3.1 Static case .....................

3.2 General case ....................

3.3 Entanglement shade ................

4 Full reconstruction using entanglement entropy and

entanglement of puriﬁcation ..............

4.1 Mapping bulk curves to CFT intervals ......

4.2 Entanglement of puriﬁcation ...........

4.3 Differential entropy and differential puriﬁcation .

Appendix: Coordinate transformations ..........

References .........................

1 Introduction and conclusions

In the quest to understand the holographic [1–4]emer-

gence of a dynamical bulk spacetime out of degrees of free-

dom living on a lower-dimensional rigid geometry, much

progress has originated from the Ryu–Takayanagi relation

[5–8]

A(

)

. (1)

Here S

denotes the entanglement entropy of a spacelike

region A in the boundary theory: S

≡−Tr(ρ

ln ρ

), with

≡ Tr

ρ the reduced density matrix associated with A,

or more precisely, with the domain of dependence of A in the

boundary theory, denoted D

. A(

) in (1) is the area

the extremal codimension-two bulk surface 

that is homol-

ogous to A (with ∂

= ∂ A).

Relation (1) informed in particular the idea of subre-

gion duality [14–20], and more speciﬁcally, the conjec-

The connection with area applies when the bulk theory is classical

Einstein gravity. For generalizations, see [9–13].

0123456789().: V,-vol

123

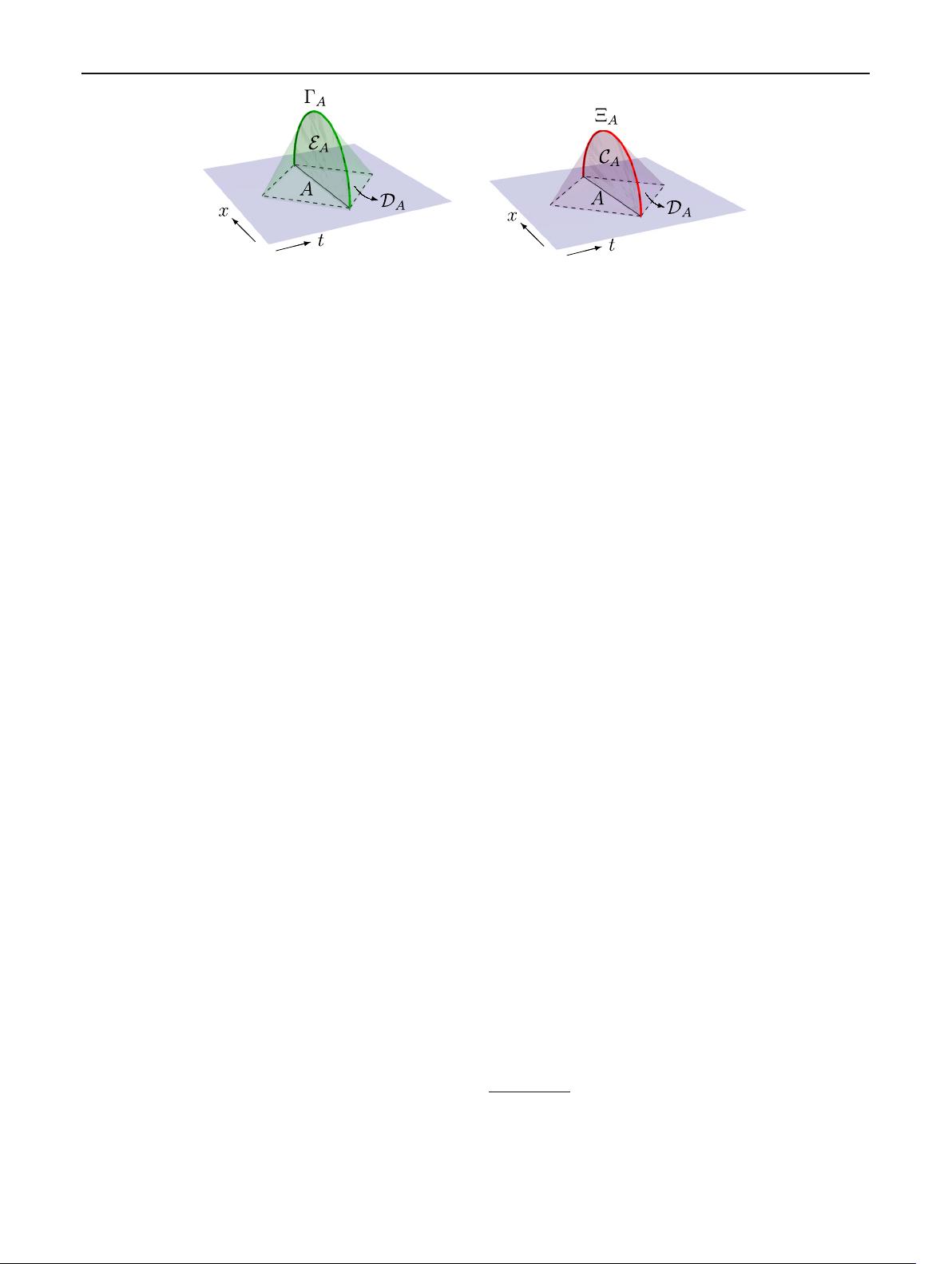
646 Page 2 of 20 Eur. Phys. J. C (2018) 78:646

Fig. 1 Schematic depiction of the entanglement wedge E

and causal

wedge

for a boundary subregion A, or equivalently, for its boundary

domain of dependence

. See the main text for the explicit deﬁni-

tions. For arbitrary bulk geometries, the entanglement wedge, bounded

by null geodesics that are shot towards the boundary from the Ryu–

Takayanagi surface 

, is larger than the causal wedge, bounded by

null geodesics that are shot into the bulk from the edge of

.The

spatial surface 

on which the latter geodesics intersect is the causal

information surface deﬁned in [17]. In a few situations 

= 

,and

the two types of wedges coincide. This happens in particular when A

is a spherical region in the vacuum of a d-dimensional conformal ﬁeld

theory, which for d = 2 gives rise to the anti-de-Sitter-Rindler wedge

considered throughout most of this paper

ture [18,21,22] that knowledge of ρ

allows full recon-

struction of the entanglement wedge of A, denoted E

and

deﬁned as the domain of dependence of any codimension-

one bulk spacelike region bounded by 

and A. See

Fig. 1a. An interesting property of the entanglement wedge

is that it is generally larger [21,22] than the bulk region

that is causally accessible from D

(i.e., the intersection in

the bulk of the causal past and the causal future of D

known as the causal wedge of A, and denoted C

. See

Fig. 1b.

For a quantum ﬁeld theory with a holographic dual, the

large-N and strong-coupling regime corresponds to the situ-

ation where the bulk theory is well approximated by Einstein

gravity coupled to a small number of light local ﬁelds. Each

of these ﬁelds φ (including the metric ﬂuctuation h

)is

dual to a simple local operator O in the boundary theory.

In this context, one aspect of reconstruction is being able to

write the boundary counterpart of the bulk ﬁeld operator φ

placed at any given bulk point x

≡ (x

, r ), with μ run-

ning over the boundary directions, and r the radial direction.

This was ﬁrst achieved with the well-known HKLL prescrip-

tion [23–29], which (at least for ball-shaped A) allows one

to deﬁne φ(x, r ) in C

by smearing O(x) over D

.Using

the connection with quantum error correction [30], a proof

was given in [31] that local operators (acting within a code

subspace) can in fact be reconstructed inside the full entan-

glement wedge E

. See also [32–34], as well as the recent

reviews [35,36].

A different aspect of reconstruction is to be able to directly

encode bulk curves or surfaces in terms of boundary data.

This question was ﬁrst addressed in [37] for the case of

global 3-dimensional anti-de Sitter spacetime (AdS

), where

an extremal surface 

is a geodesic, and its area A(

) is

a length. It was shown in that work that a generic bulk curve

at ﬁxed time, x

(λ) (with λ an arbitrary parameter), can

be represented by a family of intervals I (λ) in the bound-

ary theory, and a speciﬁc combination of the correspond-

ing entanglement entropies S

I (λ)

, known as the differential

entropy E, yields the length of the curve.

In this approach,

known as hole-ography, the intervals I (λ) are identiﬁed by

the fact that their associated bulk geodesics 

I (λ)

are tan-

gent to the bulk curve. By shrinking the curves to zero size,

one can obtain in particular the most basic ingredients of the

bulk geometry, points and distances, in terms of the pattern

of entanglement in the given state of the ﬁeld theory [40].

Hole-ography thus provides direct access to the spacetime

on which local bulk operators are to be placed, and therefore

conceptually underlies the approach summarized in the pre-

vious paragraph. This is consistent with the fact that, purely

within the ﬁeld theory, entanglement is the more fundamen-

tal substrate from which correlators of local operators arise

[41]. Hole-ography was examined in bulk dimensions higher

thanthreein[42–44], and generalized to the case of time-

dependent spacelike curves in [44]. Other extensions can be

found in [45–49].

The simplest example of an entanglement wedge is the

Poincaré patch of pure AdS

, where A is obtained by delet-

ing a single point from the boundary circle that is at play

in global AdS. In the most familiar presentation of Poincaré

AdS/CFT, a conformal transformation is used to map this

open interval to the whole real line, and the dual conformal

ﬁeld theory (CFT) then lives on 2-dimensional Minkowski

spacetime. It was recently pointed out in [48] that in this

setting hole-ography faces a serious challenge: generic bulk

curves in the Poincaré wedge have segments whose tangent

geodesics are not fully contained within the wedge, meaning

that they cannot be associated with entanglement entropies

in the CFT. See Fig. 2a. This challenge was overcome in [48]

A direct information-theoretic interpretation of E within the boundary

theory was provided in [38], and an elegant reformulation of the dual

bulk prescription was worked out in [39], employing integral geometry.

123

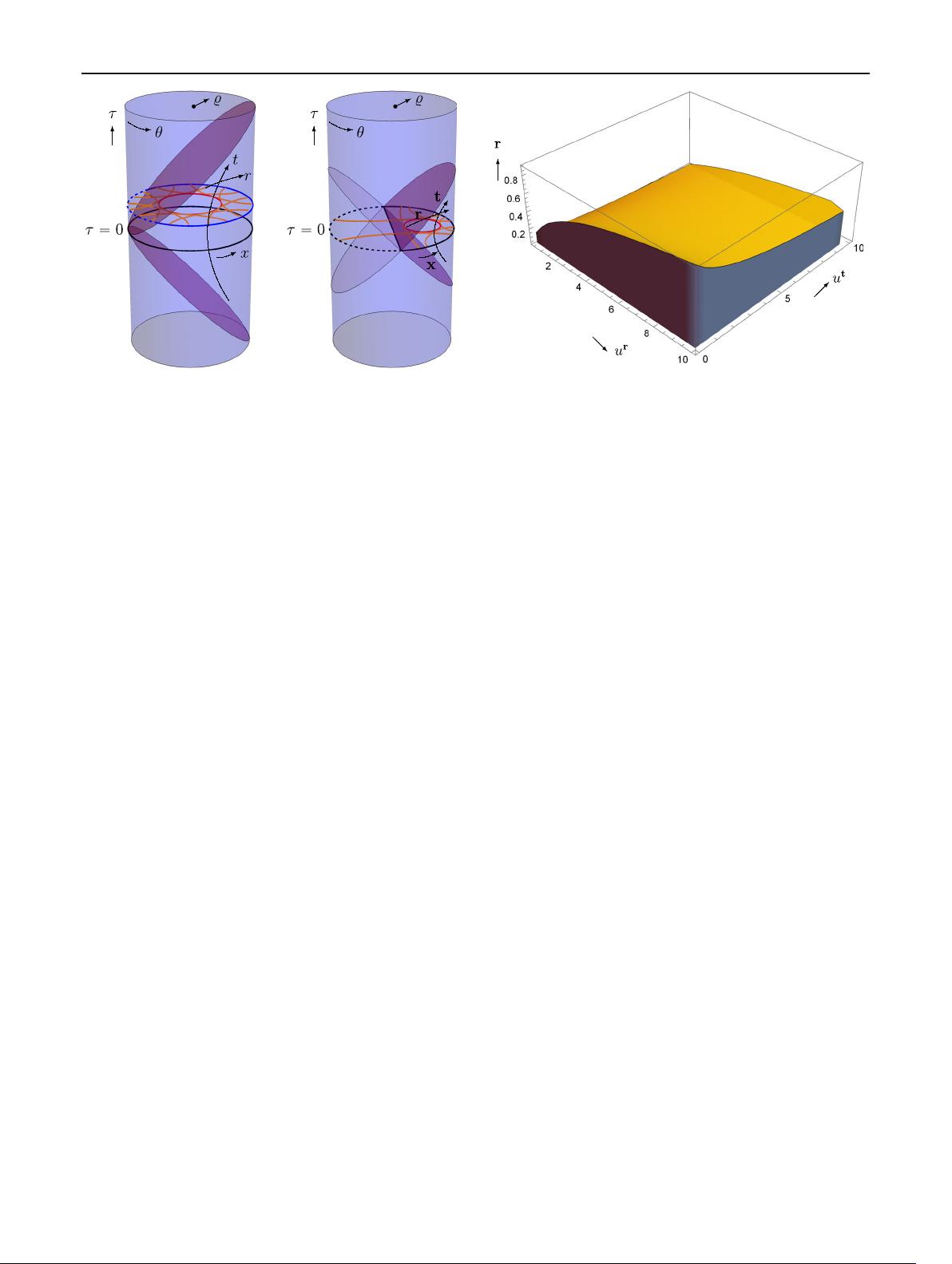
Eur. Phys. J. C (2018) 78:646 Page 3 of 20 646

Fig. 2 Each of these solid cylinders is a Penrose diagram for AdS

covered in full by the global coordinates (,τ,θ), but only in part by

the Poincaré coordinates (t, x, r) on the left, or the Rindler coordinates

(t, x, r) on the right. a Generic spatial bulk curves in the Poincaré wedge

(such as the circle shown in red) have segments whose tangent geodesics

(shown in orange) are not fully contained within the wedge. In spite of

this, a variant of hole-ography that employs ‘null alignment’ allows

their reconstruction with entanglement entropies in the CFT [48]. b A

Rindler wedge covers a smaller portion of global AdS, and in particular,

it does not contain a full Cauchy slice. A priori, it is not clear if the ‘null

alignment’ variant of hole-ography is sufﬁcient to reconstruct arbitrary

bulk curves within the Rindler wedge (such as the circle shown in red)

by using a variant of hole-ography that employs ‘null align-

ment’. The key point, discovered in [44], is that E reproduces

the length of the curve even if the intervals I (λ) are obtained

not by shooting geodesics along the direction tangent to the

curve, but along a new direction that has been shifted by

a null vector orthogonal to the curve. It was shown in [48]

that, for the segments of bulk curves that cannot be recon-

structed with the standard prescription, it is always possible

to reorient the geodesics in this manner to make sure they are

contained within the Poincaré wedge, and therefore encode

entanglement entropies. The conclusion then is that all space-

like curves in Poincaré AdS are fully reconstructible.

Since the Poincaré patch has the special property that it

contains a full Cauchy slice of global AdS, a question natu-

rally arises: when considering a smaller entanglement wedge

in AdS

, e.g., an AdS-Rindler wedge, will null alignment

again sufﬁce to ensure reconstructibility of all spacelike bulk

curves? This is the question that provides the initial moti-

vation for this paper. The fact that AdS-Rindler is smaller

than the Poincaré patch implies that there are fewer curves

that need to be reconstructed, but on the other hand, there are

more geodesics that exit the wedge. See Fig. 2b.

Our notation is established by writing the metric in the

form (2). (The transformations from global AdS

to Poincaré

and Rindler coordinates are given in Appendix A.) We

begin by working out the explicit form of the AdS-Rindler

geodesics in Sect. 2, ﬁrst at constant time in Sect. 2.1 and

Fig. 3 Entanglement shade for a Rindler wedge in AdS

, in the range

0 < u

< 10, 0 < u

< 10, having chosen the parametrization λ = x

(which implies u

= 1). The shaded region indicates the radial depths

that cannot be penetrated by geodesics with the indicated tangent vector

u, or with any other vector U obtained from it by null alignment (U =

u +n with n ·n = n ·u = 0). As expected from the analysis in the main

text, when we consider larger values of u

, corresponding to steeper

curves, the shade grows larger. On the other hand, the ﬁgure shows that

upon increasing the value of u

the shade is reduced. By symmetry, the

radial position where the shade begins is independent of the sign of u

and u

, and of course, it is also independent of the values of t and x.

The entire region shown corresponds to spacelike u

then incorporating time dependence in Sect. 2.2. With this

information in hand, we identify in Sect. 3.1 a criterion for

points on a static curve to be reconstructible using the stan-

dard tangent alignment. In Sect. 3.2 we generalize this to

time-dependent spacelike curves, incorporating the use of

null alignment, deﬁned in Eq. (30). The analysis reveals that

a curve is reconstructible only if the two conditions (45) and

(46) are obeyed. We then show in Sect. 3.3 that, even with

null alignment, curves in an AdS-Rindler wedge generically

have segments that cannot be reconstructed using entangle-

ment entropies in the CFT. The problem is that geodesics

anchored on the boundary fail to reach certain bulk regions

with a certain range of slopes. This obstruction is a gener-

alization of the well-known phenomenon of entanglement

shadows [50–55], which we call entanglement shade, and

depict in Fig. 3.

Section 4.1 delineates the problem in more detail, address-

ing the ﬁrst step for reconstruction, which is to associate our

bulk curve with a family of intervals in the boundary the-

ory. We ﬁnd that, while this can be done without difﬁculty

for open curves that are not too steep (including those that

can be shrunk down to describe points, as in [40,48]), all

closed curves and generic open curves have some number of

segments inside the entanglement shade, which by deﬁnition

cannot be encoded in terms of boundary-anchored geodesics,

and intervals in the CFT.

123

剩余19页未读，继续阅读

评论收藏

内容反馈

weixin_38606041

粉丝: 5
资源: 931

纠缠楔形重建和纠缠纯化

纠缠楔形重建的大故障

全息理论中的纠缠负性和最小纠缠楔形截面

纠缠楔形截面的注意事项

纠缠楔形截面的某些方面

楔形纠缠模块针线包

全息不等式和纯化纠缠

保形场理论的全息纯净纠缠

保形场理论中信息度量的纠缠楔

一阶校正的反射熵和纠缠楔形截面

量子零能条件，纠缠楔形嵌套和量子聚焦

纠缠在混沌系统中的扩散

异常引力及其纠缠的正性

在共形场论中推广奇异区域的纠缠熵

de Sitter前体末梢曲面和纠缠楔形

AdS / CFT中的相关度量和可蒸馏纠缠

旋转式楔形连接装置研制及其在立井提升中的应用

行业文档-设计装置-基于动压轴承教学的模块化的可变角度组合式楔形盘.zip

批量重建的模块化工具包

反射熵和全息对偶的推广

全息术中的次区域量和复杂性

关于Lifshitz时空的重建

用次区域对偶性约束高阶重力

autodyn一维楔形爆炸计算

De-Sitter全息术的一些信息理论方面

最新资源