mode samples a different area on the mirrors, the
differences of their respective ringdown times can
be associated with a spatial reflectivity distribution
function, which provides a measure for the inhomo-
geneity of the mirror coatings. Conversely, one can
use the differences in optical loss associated with
the respective transverse cavity modes to create a
“reflectivity map” of the mirrors–keeping in mind
that the contributions from the two mirrors cannot
be easily separated. Although of large historical
importance [
3,19], the coating inhomogeneity of
high-reflectivity mirrors has rarely been investi-
gated, aside from several early studies [
4] including
the first application of phase-shift CRD to the char-
acterization of mirror coatings by Herbelin et al. [
3].
In this report, we examine the influence of coating
inhomogeneity on the CRD measurement. In par-
ticular, we use the ringdown times of different trans-
verse cavity modes to creat e a “reflectivity map” for
the mirrors. We show that one can synthesize a
reflectivity map from a sum of TEM
m;n
basis func-
tions or from the spatial intensity distributions asso-
ciated with each experimentally obtained transverse
cavity mode. This may be regarded as an analogy to
the synthesis of a waveform using a sum of weighted
Fourier components.
2. Theory
The transverse mode pattern of cavity modes in
a two-mirror cavity can be described either in a
Cartesian coordinate system or in a cylindrical coor-
dinate system. In the former case Hermite–Gaussian
transverse mode patterns and their linear combina-
tions give an adequate representation of the inten-
sity distribution inside a cavity. The normalized
Hermite–Gaussian functions of order m and n can
be described as [
20–22]
HG
m
x
2
πw
2
1∕4
1
2
m
m!
p
H
m
2
p
x
w
exp
−x
2
w
2
m 0; 1; 2; 3; …
HG
n
y
2
πw
2
1∕4
1
2
n
n!
p
H
n
2
p
y
w
exp
−y
2
w
2
n 0; 1; 2; 3; …; (1)
where H
m
x and H
n
y are Hermite polynomial
functions of order m and n, respectively, and w is
the beam waist of the lowest order mode. The inten-
sity distribution of each TEM
m;n
mode can be calcu-
lated from the Hermite–Gaussian basis functions
I
m;n
x; yI
0
m;n
HG
m
x
2
HG
n
y
2
: (2)
The normalization factors in Eq. (
1) assure that for
each mode
1
Z
∞
x−∞
HGx
2
dx
Z
∞
y−∞
HGy
2
dy: (3)
And therefore,
I
0
I
0
m;n
Z
∞
x;y−∞
I
m;n
x; ydxdy: (4)
In the analysis of the experimental data we scale the
spatially integrated intensity of each mode to the
same value, I
0
. Examples of calculated I
m;n
x; y
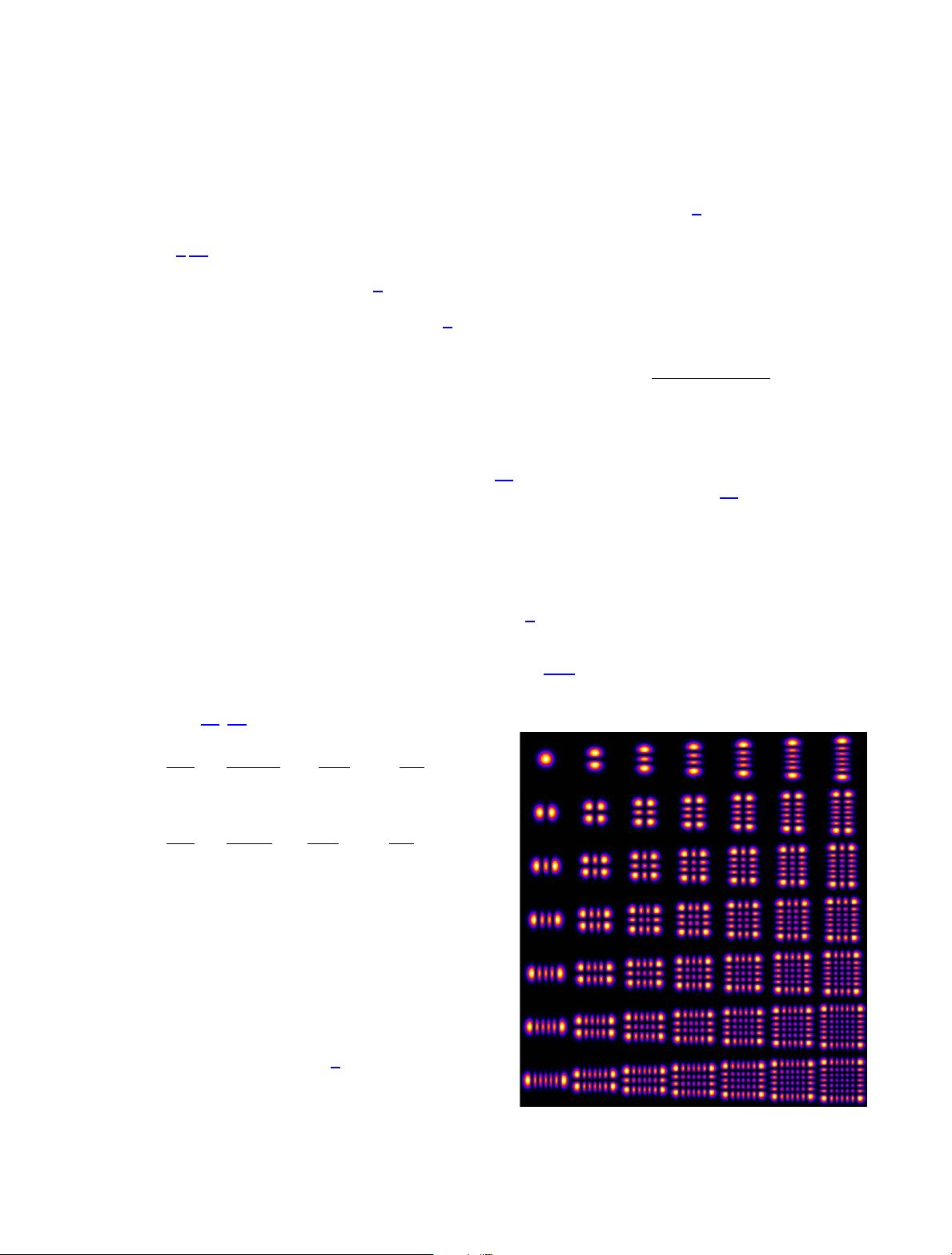
functions are given in Fig.
1.
We intend to obtain information about the mirror
coating’s homogeneity from a “reflectivity map.” The
transverse modes on each of the mirrors can be added
incoherently and in the limiting case of a very large
number of transverse modes the sum of all their
intensities covers the mirror surface smoothly with
a maximum on the cavity axis:
¯
Ix; y
P
N;M
n;m0
I
m;n
x; y
N 1M 1
: (5)
The size of the area that can be inte rrogated in this
manner depends on the size of the highest order
HG-mode, which is about 4w
2
N 1
1∕2
M 1
1∕2
[22]. It is well-known that Hermite–Gaussian func-
tions form a complete basis set [
22], and the interrog-
ation area as well as the spatial resolution can be
increased by including more modes in the analysis.
In a practical application the number of available
mode functions is finite. We used N M 6 for 49
TEM modes in the simulation and a total of 13 or 15
modes in the present experiments. As indicated in
Eq. (
4), we give each mode the same weight.
When the mirror surface exhibits defects in the
coating, the reflectivity of each mode is reduced.
Figure
2(A) shows the location of a simulated defect
as the product,
¯
Ix; y · Rx; y, which is equivalent to
n,0 n,1 n,2 n,3 n,4 n,5 n,6
0,m
1,m
2,m
3,m
4,m
5.m
6,m
Fig. 1. Simulated intensity distribution functions for a set of
Hermite–Gaussian transverse cavity modes.
2918 APPLIED OPTICS / Vol. 53, No. 13 / 1 May 2014



 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功