BalancePreferenceswithPerformanceinGroupRoleAssignment资源-CSDN文库

15 浏览量 2021-02-21 23:17:01 上传评论收藏 1.7MB PDF 举报

资源推荐

资源详情

资源评论

This article has been accepted for inclusion in a future issue of this journal. Content is final as presented, with the exception of pagination.

IEEE TRANSACTIONS ON CYBERNETICS 1

Balance Preferences with Performance

in Group Role Assignment

Dongning Liu, Member, IEEE, Yunyi Yuan, Haibin Zhu, Senior Member, IEEE,

Shaohua Teng, and Changqin Huang, Member, IEEE

Abstract—Role assignment is a critical element in the

role-based collaboration process. There are many factors to con-

sider when decision makers undertake this task. Such factors

include a decision maker’s preferences and the team’s perfor-

mance. This paper proposes a series of methods, relative to these

factors, to solve the group role assignment with balance problem

through an association with the one clause at a time approach

that is a well-accepted and logic-based association rule mining

method. The proposed methods are veriﬁed by simulation exper-

iments. The experimental results present the practicability of the

proposed solutions. Using the proposed methods, decision mak-

ers need only to establish coarse-grain preferences. The ﬁne-grain

preferences can be mined. Furthermore, a balance is obtained

between the ﬁne-grain preferences and the team’s performance.

Index Terms—Assignment, group role assignment (GRA),

one clause at a time approach (OCAT), preference, role-based

collaboration (RBC), team performance.

I. INTRODUCTION

OLE assignment has been revealed as a complex pro-

cess throughout the life cycle of role-based collabora-

tion (RBC) [1], i.e., agent evaluation, role assignment, role

playing, and role transfer. Group role assignment (GRA) seeks

an optimal role-to-agent assignment based on the results of

agent evaluations [2] and greatly affects collaboration efﬁ-

ciency and the degree of satisfaction of members involved in

RBC.

RBC is a very different topic compared with role-based

access control (RBAC) [3]–[5] that is a well-known approach

to conduct system protections. The speciﬁcations of roles

in RBC are also different from those in RBAC. Previous

Manuscript received December 15, 2016; revised April 8, 2017; accepted

June 6, 2017. This work was supported in part by the National Natural

Science Foundation of China under Grant 61402118 and Grant 61370229,

in part by the Natural Sciences and Engineering Research Council, Canada,

under Grant RGPIN262075-2013, in part by the S&T Project of Guangdong

Province under Grant 2016B010108007 and Grant 2016B010109008, in part

by the S&T Project of Guangzhou under Grant 201604020145, and in part by

GDUPS (2015). This paper was recommended by Associate Editor Q. Shen.

(Corresponding author: Haibin Zhu.)

D. Liu, Y. Yuan, and S. Teng are with the School of Computer

Science and Technology, Guangdong University of Technology,

Guangzhou 510006, China (e-mail: liudn@gdut.edu.cn; 970208091@qq.com;

shteng@gdut.edu.cn).

H. Zhu is with the School of Management and Engineering, Nanjing

University, Nanjing 210093, China, and also with the Department of Computer

Science and Mathematics, Nipissing University, North Bay, ON P1B 8L7,

Canada (e-mail: haibinz@nipissingu.ca).

C. Huang is with the School of Information Technology in Education,

South China Normal University, Guangzhou 510631, China (e-mail:

cqhuang@zju.edu.cn).

Digital Object Identiﬁer 10.1109/TCYB.2017.2715560

work in RBC has clariﬁed the differences between RBAC and

RBC [1], [6]. In short words, RBC utilizes roles as fundamen-

tal mechanisms to facilitate collaboration but RBAC access

control. Roles in RBC specify both rights and responsibilities

but those in RBAC emphasize rights [1], [6].

GRA is itself a complex problem where the exhaustive

search algorithm has an exponential increase in complexity.

In our previous work, an efﬁcient algorithm was developed

by using the Hungarian algorithm (also called Kuhn–Munkres

algorithm [7], [8]) [9]. That means GRA becomes a straight-

forward process, which is devoted to ﬁnding the maximum

team performance.

Note that in addition to individual agent role perfor-

mance, there are other factors such as preferences that

determine whether roles are performed effectively by agents.

Psychologically, preferences could be considered as an indi-

vidual’s attitude toward a set of objects. Such an atti-

tude is typically reﬂected in an explicit decision-making

process [5], [10]. Alternatively, one could interpret the term

preferences to mean the judgment of a decision maker in the

sense of liking or disliking an agent [11], [12]. Preferences

may also express those factors that are highly intelligent and

difﬁcult to state. For example, in a battleﬁeld, the prefer-

ences of the commander is more important than the objective

evaluations of soldiers and groups of soldiers. Therefore,

in role assignment, we need to consider not only the team

performance but also the preferences of decision makers.

However, in the real-world, preferences and performances

are often in conﬂict. For example, in a company, manager

A may prefer staff member B, but if A considers objective

evaluations, staff member C may be more competitive. How

should manager A choose one from B and C? If there are teams

involved and many tasks to undertake, the manager’s decision

making is far more difﬁcult. Moreover, how does a supervisor

present his/her preferences? If these preferences are coarse-

grained, how does an analyst reﬁne and balance them with

team performance?

Although there are many investigations of assignment prob-

lems in different applications [13]–[17], we still require an

assignment solution that effectively balances preferences with

team performance. Therefore, the GRA with balance (GRAB)

problem is formed. The primary objective of this paper is

to provide a series of practical solutions to the GRAB prob-

lem. Although such problems arise in the research of RBC,

they are also important and challenging in the domains of

administration, production, and engineering.

2168-2267

 2017 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission.

See http://www.ieee.org/publications_standards/publications/rights/index.html for more information.

This article has been accepted for inclusion in a future issue of this journal. Content is final as presented, with the exception of pagination.

2 IEEE TRANSACTIONS ON CYBERNETICS

The contributions of this paper include: 1) the concise for-

malization of the GRAB problem; 2) a fundamental approach

to solving the GRAB problem by providing a feasible

solution; and 3) a series of improvements to the fundamen-

tal approach by combining with the one clause at a time

approach (OCAT) [43], which is an iterative, and logic-based

association rule mining method.

The proposed methods require a decision maker to estab-

lish only coarse-grain preferences. The ﬁne-grain preferences

will be mined, and then the balance between the performance

and the ﬁne-grain preferences is established by using a GRAB

solution. For example, if a manager expresses his/her coarse-

grain preferences as like and dislike, our proposed method can

conduct GRA with ﬁne-grain preferences, or Likert-scale pref-

erences, i.e., strongly like, like, neutral, dislike, and strongly

dislike.

This paper is organized as follows. Related work is dis-

cussed in Section II. It describes a real-world scenario related

to the proposed problem in Section III and formally speciﬁes

the GRAB problem with the revised environments—classes,

agents, roles, groups, and objects (E-CARGO) model in

Section IV. Section V presents the fundamental solution and

Section VI explains how preferences can be mined and reﬁned

by OCAT. After that, Section VII proposes two methods to

improve the fundamental solution by combining with OCAT to

solve the GRAB problem. Section VIII is used to supplement

Section VII and deals with the negative association preference

set while the former processes the positive set. Section IX

illustrates experiments and analyzes their results. This paper

concludes and points out future works in Section X.

II. R

ELATED WORK

Preference research is an important and challenging topic

in decision theory, operation research, computer science, eco-

nomics, etc. [19]–[23]. Currently, such research is more

popular than ever. As for human’s behavior or performance,

preference research can be divided into two aspects.

1) Preference and personal behavior, such as recom-

mendations, retrieval, social network, and customer

classiﬁcation [24], [25].

2) Preference and team performance. In this paper, we

mainly focus on the latter.

In the research of preferences and team performance,

Salterio [26] showed that managers respond to their own

incentives and preferences when subjectively evaluating per-

formance. He indicated that performance evaluation biases

affect not only current performance ratings, but also future

employee incentives. Mohammadi et al. [27] proposed a met-

ric for evaluating the performance of user preferences based on

evolutionary multiobjective algorithms by deﬁning a preferred

region. Olaverri-Monreal et al. [28] investigated whether

drivers would like to have additional in-vehicle information

that can be also found in other mobile environments. They

also studied the driving performance with the preferred loca-

tions for in-vehicle information. Zeydan et al. [29] considered

both qualitative and quantitative variables in evaluating per-

formances for selection of suppliers based on efﬁciency and

effectiveness in one of the biggest car manufacturing factory

in Turkey. Melville et al. [30] revealed that studies examining

the association between information technology and organi-

zational performance are divergent in how they conceptualize

key constructs and their interrelationships.

Because preferences and performances have different mea-

surements, many researches always deal with task assignments

as a multiobjective problem [18], [31]–[33]. However, in this

paper, based on the introduction of roles, RBC and GRA,

via normalization, we use methods of dynamic preference

weights of agents, such that, we can consider both preferences

and performance intuitively. This is in favor of ﬁnding the

balance points between preferences and performance. Simply,

existing methods for solving role assignment problems cannot

be used in dealing with the proposed GRAB problem.

As regards to role assignment, some related research

work focuses on role assignment for agents in multiagent

systems [34], [35] or nodes in networked systems [36].

Bhardwaj and Chandrakasan [36] presented a real-world

application that requires role assignment. Dastani et al. [34]

presented research on the determination of conditions under

which an agent can perform a role. Durfee et al. [37] pro-

posed a new formulation of the team formation by modeling

the assignment and scheduling of expert teams as a hybrid

scheduling problem. Shen et al. [38] proposed a multicri-

teria assessment model capable of evaluating the suitability

of individual workers for a speciﬁed task according to their

capabilities, social relationships, and existing tasks. We

formally identiﬁed a group of problems in role assignment.

We propose a formal provision of taxonomy for collective

GRA and an indication of the complexities arising from this

type of problem through simulations and experiments. Based

on these, we successively deal with role transfer, adaptive,

conﬂicts problem [1], [2], [9], [39]–[41], etc.

The aforementioned research indicates a strong need to fun-

damentally investigate role assignments to balance between

preferences and performance.

III. R

EAL-WORLD SCENARIO

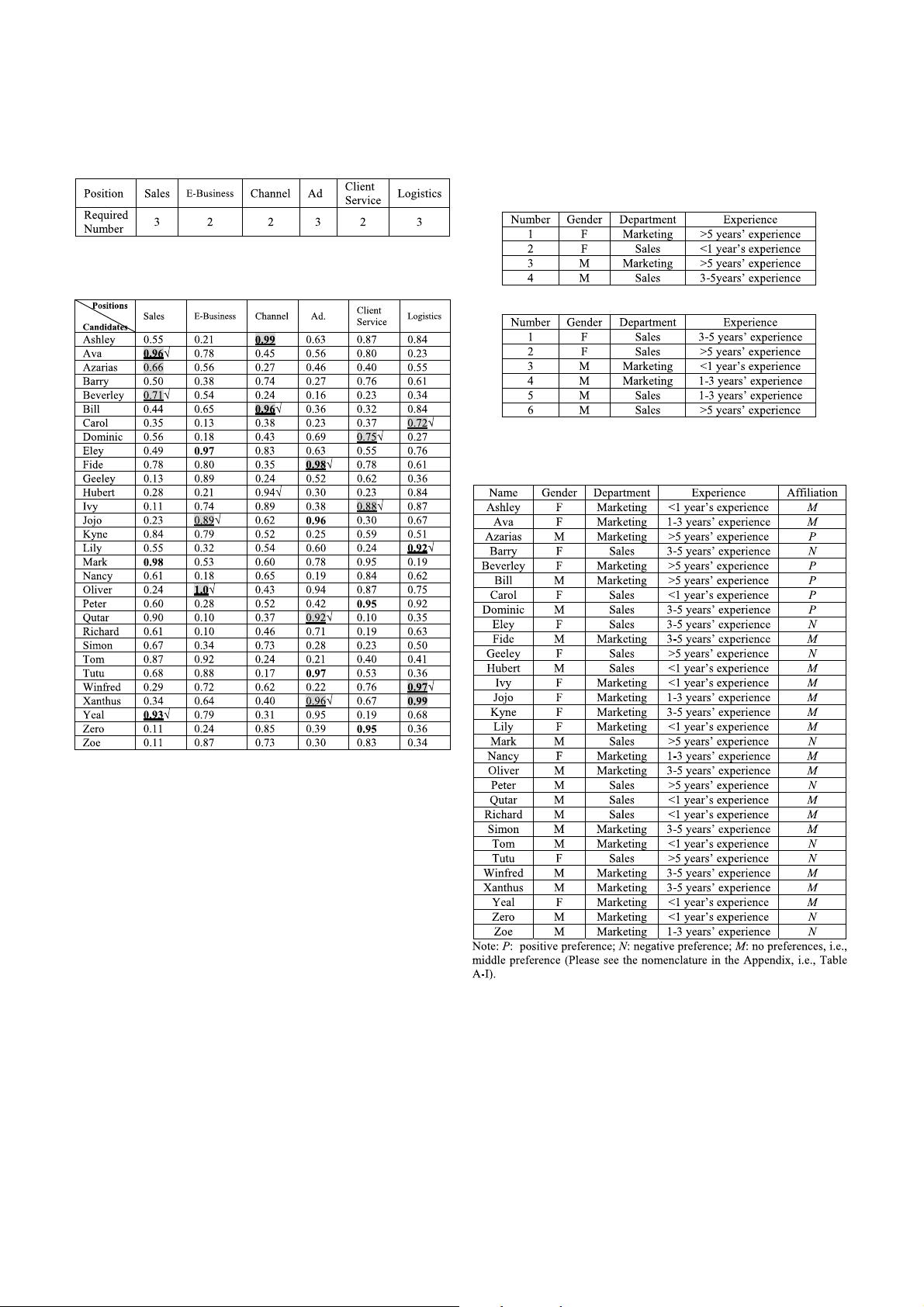
Company X hopes to release a new product. Ann, the Chief

Executive Ofﬁcer, asks Bob, the Human Resources (HR) ofﬁ-

cer, to organize a team of employees for the project. Bob drafts

a team position list (Table I) and a candidate staff shortlist

shown as column 1 in Table II. Then, Bob initiates an evalu-

ation process by asking branch ofﬁcers to evaluate employees

for each possible position (Table II). As a routine policy, the

new team leader’s preferences are considered in the evalu-

ation of team members. Therefore, Bob requests Chris, the

Product Manager and Team Leader, to offer her preferences

in the recruiting process. To avoid personal conﬂict with team

members, Chris avoids providing a list of names. Instead,

she offers a list of preferences for staff properties (Table III).

Chris’ demand is reasonable because the nonobjective factors,

such as gender, experiences and personalities of team members

affect the quality of the work. Based on Chris’ preferences,

Bob creates Table IV based on staff’s properties and Table III.

Now he obtains the preferred staff list (the rightmost column

This article has been accepted for inclusion in a future issue of this journal. Content is final as presented, with the exception of pagination.

LIU et al.: BALANCE PREFERENCES WITH PERFORMANCE IN GRA 3

TABLE I

REQUIRED POSITIONS

TABLE II

ANDIDATES AND POSITION EVALUATIONS

of Table IV). He must assign the most qualiﬁed candidates

to jobs to maximize the team performance while satisfying

Chris’ preferences.

The challenge to Bob is that there are not enough positively

preferred staff members to fulﬁll the required positions. On

the other hand, as a qualiﬁed HR ofﬁcer, Bob knows that he

must consider a balance between overall team performance

and Chris’ preferences.

Bob thinks that he can lower the performance scores of

Chris’ negatively preferred staff appropriately. If so, there will

be an impact on the opportunities for staff to be chosen.

Therefore, Bob sets the weight of Chris’ negative prefer-

ences to 0.5 and the weight for positive preferences to 1.

Performance scores in Table II would therefore be adjusted,

i.e., if one’s score for a position is 0.9, then the score is

0.9×0.5 = 0.45 if she/he is in the negative preference list. Note

if she/he is in the positive preference list, the score remains

0.9. This can lower the chances of negatively preferred staff

to be chosen based on Chris’ preferences.

If Bob wants to choose staff according to the newly updated

performance score list, he still needs to consider those who are

not in Chris’ preference list, such as Ashley, Jojo, Richard, etc.

TABLE III

CHRIS’PREFERENCES OF STAFF’S PROPERTIES.(a)POSITIVE

PREFERENCE.(b)NEGATIVE PREFERENCE

(a)

(b)

TABLE IV

TAFF’S PROPERTIES AND PREFERENCES AFFILIATION

What weight should be assigned in this situation? If this

weight is too big, it will reduce chances of positively preferred

staff. On the other hand, if the weight is too small, positively

preferred staff with low-performance scores may be chosen.

As a result, the overall team performance is lowered.

In consideration of the above situations, Bob suggests that

a satisfactory solution, in light of such a challenge, may

require a signiﬁcant amount of time. Fortunately, Ann, as

an experienced administrator, understands the complexity of

剩余13页未读，继续阅读

评论收藏

内容反馈

weixin_38576811

粉丝: 6
资源: 890

Balance Preferences with Performance in Group Role Assignment

Windows Server 2008 Group Policy Preferences

preferences

Preferences

数据存储之Preferences

allegro_user preferences详解1-2

Android代码-Multiplatform-Preferences

Exploiting Group Recommendation Functions for Flexible Preferences

Android代码-preferences-helper

Hootsuite-2021年社交趋势报告（英文）-20212-54页.pdf

Android Preferences保存数据的简单实例

Android代码-rx-preferences

A GARCH option pricing model with α-stable innovations

利用Shared Preferences，在2个不同的Activity传递数据

Android Preferences

Android代码-android-secure-preferences

Eclipse Preferences for python

Android代码-一个快速方便地访问Android Shared preferences 库。

Teachers' use and children's preferences of rewards in elementary school

1613104635615_Tuning Dampers for Ride and Handling of Production Vehicles.pdf

android 数据存取Preferences

Android 使用Shared Preferences进行数据存储-样例.rar

Learning.Data.Mining.with.Python.1784396052

Preferences_android_

Android代码-secure-preferences

movie_preferences

Algorithmics of Matching Under Preferences

shared-preferences for flutter

android 定制preferences布局和自定义对话框（左边带图标的preferences）

最新资源