对静态QCD势进行超软校正的Renormalon自由部分资源-CSDN文库

Open

Access

187 浏览量 2020-04-03 09:43:51 上传评论收藏 436KB PDF 举报

资源推荐

资源详情

资源评论

Physics Letters B 783 (2018) 350–356

Contents lists available at ScienceDirect

Physics Letters B

www.elsevier.com/locate/physletb

Renormalon free part of an ultrasoft correction to the static QCD

potential

Hiromasa Takaura

Department of Physics, Tohoku University, Sendai, 980–8578, Japan

a r t i c l e i n f o a b s t r a c t

Article history:

Received

21 December 2017

Received

in revised form 19 May 2018

Accepted

9 July 2018

Available

online 12 July 2018

Editor:

J. Hisano

Keywords:

QCD

Summation

of perturbation theory

Perturbative calculations of the static QCD potential have the u = 3/2 renormalon uncertainty. In the

multipole expansion performed within pNRQCD, this uncertainty at LO is known to get canceled against

the ultrasoft correction at NLO. To investigate the net contribution remaining after this renormalon

cancellation, we propose a formulation to separate the ultrasoft correction into renormalon uncertainties

and a renormalon independent part. We focus on very short distances 

QCD

r  0.1and investigate the

ultrasoft correction based on its perturbative evaluation in the large-β

approximation. We also propose

a method to examine the local gluon condensate, which appears as the ﬁrst nonperturbative effect to the

static QCD potential, without suffering from the u = 2 renormalon.

(http://creativecommons.org/licenses/by/4.0/). Funded by SCOAP

1. Introduction

The static QCD potential plays an important role to investigate

the QCD dynamics. It has been investigated extensively by using

perturbation theory, effective ﬁeld theory and lattice simulations.

In perturbative evaluations, perturbative coeﬃcients are ex-

pected

to show factorial behaviors at large orders. Such divergent

behaviors, in particular those related to a positive renormalon, in-

duce

ambiguity to the resummation of the perturbative series [1].

For the static QCD potential, renormalons are located at positive

half integers in the Borel u-plane. The ﬁrst renormalon at u =1/2

causes

an uncertainty to the r-independent constant of the poten-

tial.

This renormalon is known to get canceled in the total energy

(i.e. the sum of the QCD potential and twice the pole mass) within

usual perturbation theory once the pole mass is expressed as a

perturbative series in terms of the MS mass.

In considering cancellation of the other renormalons, it is useful

to adopt the effective ﬁeld theory (EFT) known as potential non-

relativistic

QCD (pNRQCD) [2]. The renormalons are expected to get

canceled ultimately in the multipole expansion performed in this

EFT. The leading order (LO) term of this expansion is the singlet

potential V

(r), which behaves as O(1/r) and can be evaluated in

perturbation theory. The renormalons for V

are located at positive

half integers as mentioned above, and the leading r-dependent un-

E-mail address: t_hiromasa@tuhep.phys.tohoku.ac.jp.

certainty is caused by the u =3/2renormalon. The next-to-leading

order (NLO) term in the multipole expansion, which we denote by

δE

, represents the dynamics at the ultrasoft scale ∼ α

−1

)/r

and

its explicit r-dependence is O(r

). In Ref. [2], it was pointed

out within the leading-logarithmic approximation that the u = 3/2

renormalon

exists in δE

and it cancels against the u = 3/2renor-

malon

of V

. In Ref. [3], the perturbative evaluation of δE

the large-β

approximation was completed, and again, the u = 3/2

renormalon

cancellation was conﬁrmed.

Although

the u = 3/2renormalon cancellation has been estab-

lished,

it has not been clariﬁed what remains in the NLO calcula-

tion,

+δE

, as a consequence of this renormalon cancellation.

In particular, the net contribution to δE

remaining after this can-

cellation

has not been made clear. In this Letter, we investigate the

net contribution to δE

, which is not affected by the renormalon

cancellation. The distances considered here are 

QCD

r  0.1, where

δE

as well as V

can be evaluated perturbatively since the ul-

trasoft

scale satisﬁes α

−1

)/r  

QCD

. In this range, the leading

nonperturbative correction is given through the local gluon con-

densate.

In order to examine the local gluon condensate, the per-

turbative

part, i.e. V

+δE

, should be clearly known in advance.

Although the currently available order of perturbative expansion

is far from the (expected) relevant order to the u = 3/2renor-

The appearance of this nonperturbative effect has been ﬁrst considered in

Refs. [4–6], and can be understood in a systematic expansion of pNRQCD [2].

https://doi.org/10.1016/j.physletb.2018.07.014

0370-2693/

SCOAP

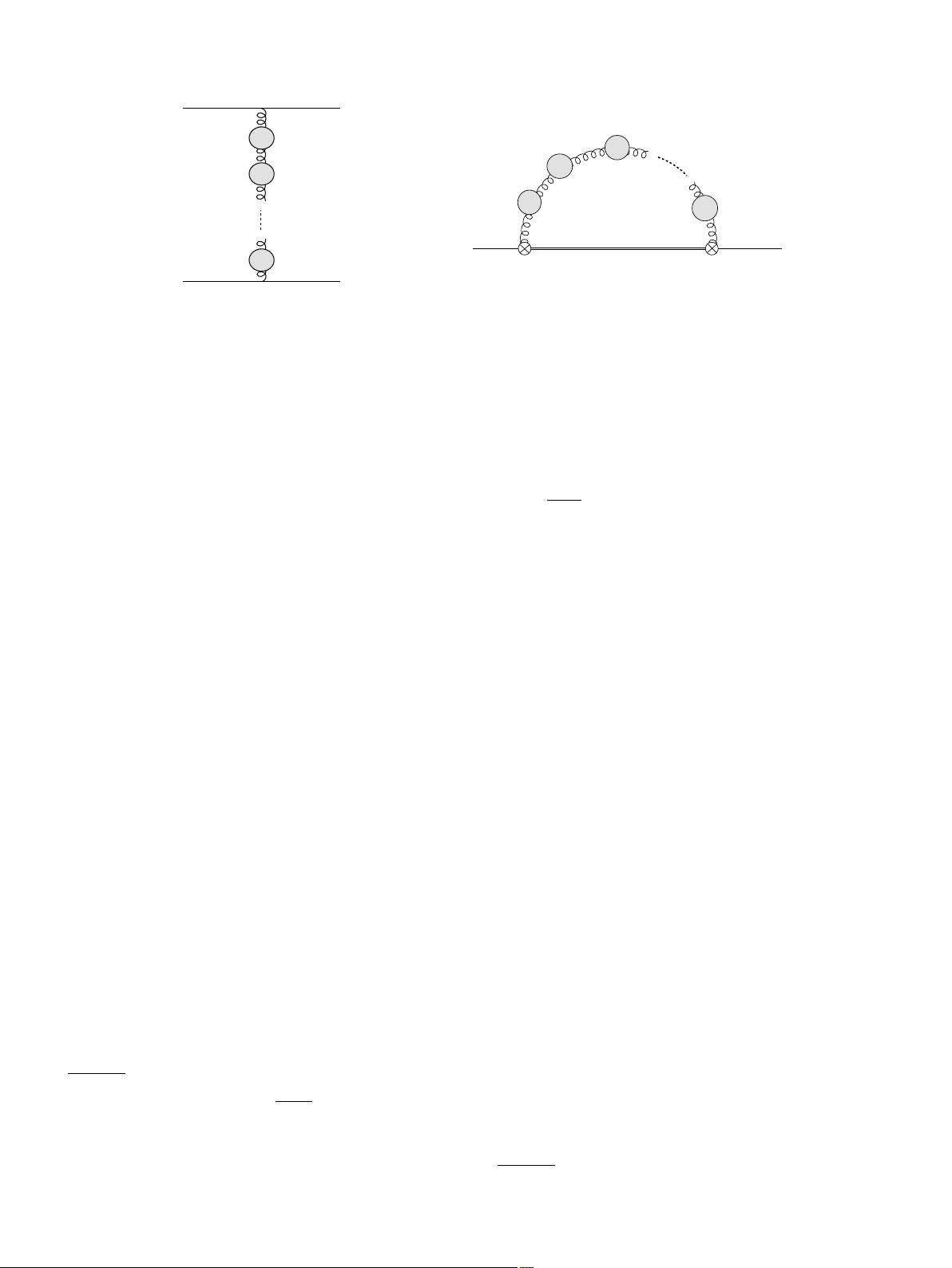
H. Takaura / Physics Letters B 783 (2018) 350–356 351

Fig. 1. Diagrams for the singlet potential (left) and δ E

(right) in the large-β

approximation.

malon,

this Letter aims at promoting theoretical understanding of

the static QCD potential without suffering from renormalons.

investigate the net NLO correction, we propose a formu-

lation

to separate δ E

into its renormalon uncertainties and a

renormalon free part. In perturbative evaluations, the large-β

ap-

proximation

is used. For the LO term V

, a renormalon separation

has been performed in Ref. [7]. In this Letter, we will see that the

u = 3/2renormalon uncertainty of V

separated out in Ref. [7]is

canceled against that of δ E

identiﬁed here. As a result, a the-

oretical

expression after the u = 3/2renormalon cancellation is

obtained by the sum of the renormalon free parts of V

and δE

Each is presented in an analytic form in this Letter.

Once the renormalon separation of δ E

is performed, it is

straightforward to cope with the residual renormalon at u =2. This

renormalon in δ E

(found explicitly in Ref. [3]) is consistent with

the fact that the local gluon condensate appears as the ﬁrst non-

perturbative

effect. The u = 2renormalon induces an O(

QCD

)

error to V

+ δE

, which is the same magnitude as the term of

the local gluon condensate. Hence, the u = 2renormalon is an

obstacle in examining the local gluon condensate even after the

u = 3/2renormalon is removed. We circumvent this problem by

including the u = 2renormalon uncertainty of δE

in the local

gluon condensate, which results in the cancellation of the u = 2

renormalon

in the local gluon condensate. This renormalon can-

cellation

is explicitly conﬁrmed in this Letter using the large-β

approximation. As a result, one can obtain the expansion in r up

to the order including the local gluon condensate such that each

term does not have the u = 3/2 and u = 2renormalons. Such a re-

sult

can be used to extract the local gluon condensate numerically,

for instance, by comparing lattice simulations with the calculation

presented here.

Our

formulation to extract a renormalon free part of δE

an extension of Refs. [8,9], which propose the method to extract a

renormalon free part in the leading term in operator product ex-

pansion

(see Ref. [10]as a related work). The characteristics of our

formulation is to introduce explicit cutoff scales, which are com-

patible

with the concept of the EFT.

This clariﬁes intuitively how

renormalon uncertainties appear and also vanish when combined

with contributions of different energy scales. In particular, we will

see how a renormalon free part is identiﬁed in connection with

the cutoff scales.

For the singlet potential V

, the relevant perturbation order to the u = 3/2

renormalon

is roughly estimated as n

∗

6π

−1

)

∼ 20, while the exact series is

currently known up to O(α

The u = 1/2renormalon uncertainty in V

is just omitted as it changes only

the r-independent constant.

The analytical result for V

that is free from renormalons has been given in

Ref. [7].

The cutoff scale dependence vanishes in the ﬁnal results.

2. Extraction of renormalon free part

In the multipole expansion performed within pNRQCD, the

static QCD potential is represented as [2]

QCD

(r) = V

(r) +δE

(r) +... , (1)

δE

(r)

=−

πα

∞



dt e

−iV (r)t





r ·



(t)ϕ

adj

(t, 0)



r ·



(0), (2)

where the dots denote higher order corrections in r; V (r) =

(r) −V

(r) denotes the difference between the octet and singlet

potentials, which speciﬁes the ultrasoft scale;



is the ultrasoft

chromoelectric ﬁeld. See Ref. [2]for details. In the following, we

evaluate V

and δE

in perturbation theory especially using the

large-β

approximation [11,12]. The corresponding diagrams are

shown in Fig. 1.

Let

us ﬁrst sketch what we will do in the following. We in-

troduce

cutoff scales μ

and μ

to divide the energy region:



QCD

μ

V  μ

r

−1

. We deﬁne V

as a soft quantity by

restricting the gluon momentum to be higher than μ

. Similarly,

we deﬁne δE

as an ultrasoft quantity by requiring the relevant

momentum p to be μ

< p < μ

. Accordingly, we perform the

multipole expansion as

QCD

(r) = V

(r;μ

) +δE

(r;μ

, μ

) +... . (3)

For the singlet potential V

(r; μ

), we follow the separation per-

formed

in Ref. [7]

(r;μ

) = V

(r) +C

(μ





(4)

where V

is a renormalon free part and has a Coulomb+lin-

ear

form. The leading cutoff dependence in V

(r, μ

), C

(μ

∼

, is caused by the u = 3/2renormalon. In this Letter, we show

that δE

(r; μ

, μ

) can be decomposed as

δE

(r;μ

, μ

) ∼δ E

(r) −C

(μ





(5)

where δE

(r) is independent of μ

and μ

and is free from renor-

malons.

As a result, in the multipole expansion (3), we have

QCD

(r) = V

(r) +δE

(r) +O





(6)

In this way, we can obtain a net contribution up to NLO, where

each term does not have renormalon ambiguity.

In Eq. (4), we omit the r-independent constant related to the u = 1/2renor-

malon.

剩余6页未读，继续阅读

评论收藏

内容反馈

weixin_38570459

粉丝: 3
资源: 931

对静态QCD势进行超软校正的Renormalon自由部分

红外超对称模型中的红外renormalon。

压缩时空中的Renormalon结构

用正态减法确定静态QCD势

在LHC上对WZ散射进行QCD和电弱校正

对大型强子对撞机具有轻子衰变的WZZ产物进行NLO QCD + NLO EW校正

标准模型EFT中的QCD校正适合WZ和WW生产

大型强子对撞机的轻子衰变导致三阶W产生的下一阶QCD和电弱校正

共振区域中对Drell-Yan过程的主要混合QCD电弱O（αsα）校正

混合QCD-EW对胶子聚变中希格斯玻色子产生的贡献的高阶校正

全息QCD相图与相互和n部分信息之间的相互作用

在物理点上对晶格QCD的μon异常磁矩进行强等旋断裂校正

与矢量玻色子相关的NLO QCD + EW校正双光子产生

通过胶子聚变对W + W −产生的QCD校正

来自复晶格QCD势的中等P波石英

广角康普顿散射中对软观众的QCD辐射校正

强子对撞机通过胶子聚变生产希格斯对：NLO QCD校正

QCD校正胶子融合中矢量玻色子对的产生，包括在LHC上对壳外希格斯干涉的影响

HAL QCD的波函数当量法中的当前矩阵元素

静态夸克自由能对μB和Nf = 2 + 1 QCD的交越温度的依赖性

QCD中平面两环五部分散射振幅的解析形式

在TeV尺度引力模型中对Drell-Yan截面的NNLO QCD校正

对包括6维算子在内的希格斯对产生的NLO QCD更正

关于对重胶子传播子的QCD RFT校正

QCD对大量颜色八位字节矢量玻色子对产生的校正

CEPC对e + e−。→μ+ μ−H的混合电弱QCD校正具有有限宽度效应WC和YJ的工作部分文章

Padé近似值对强子τ衰变的高阶QCD校正

最新资源