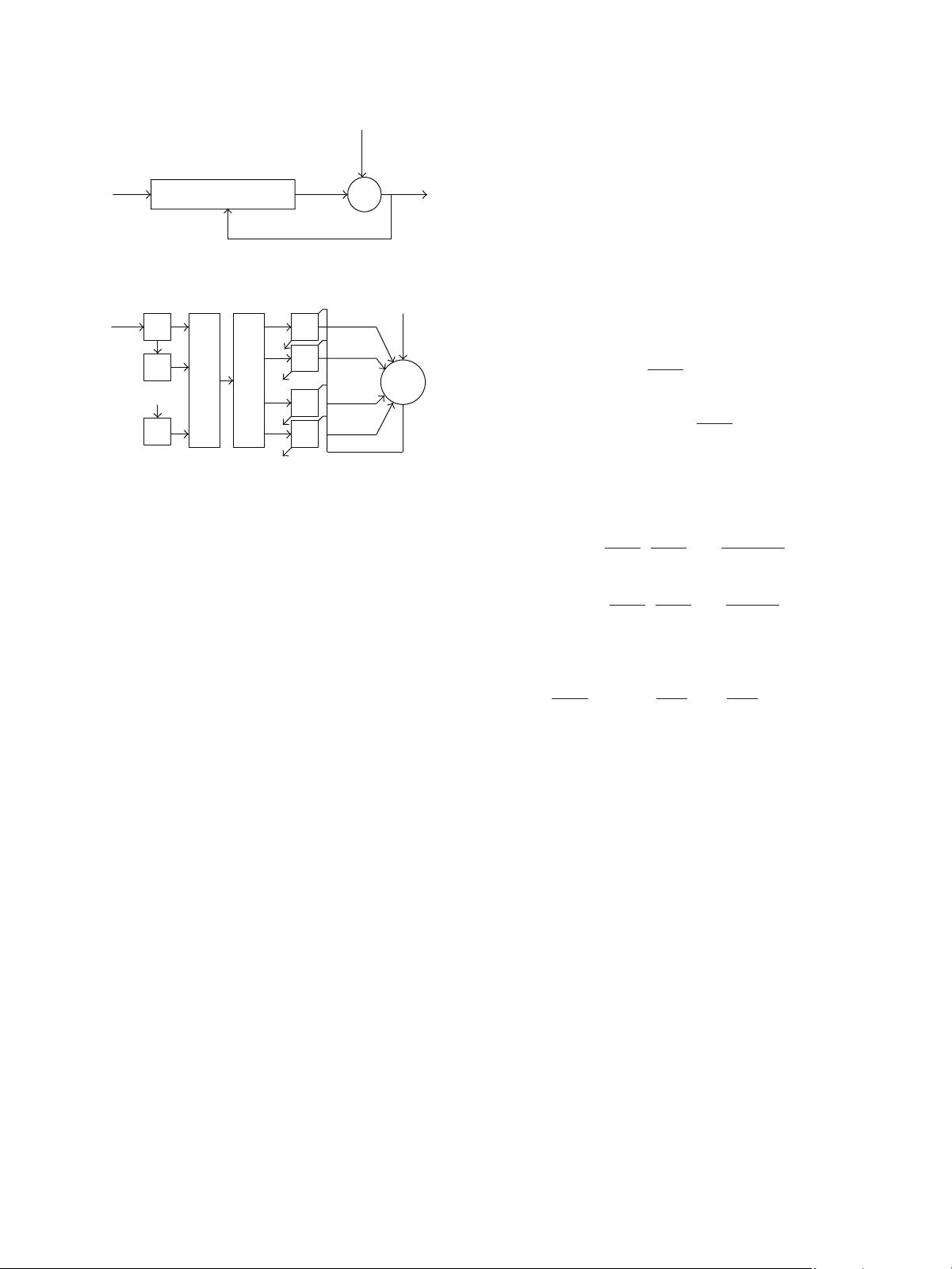
这篇文章主要讲述了小波自适应算法及其在磁流变弹性体(MRE)噪声控制系统中的应用。文章的主要内容包括:传统自适应算法在主动噪声控制系统中的局限性,基于小波的自适应算法的提出和研究,以及这两种算法在包括MRE在内的噪声控制系统中的应用。模拟结果显示,基于小波的分解最小均方算法(D-LMS)和分解重建最小均方算法(DR-LMS)能够显著提高MRE控制系统的降噪性能,相比于传统的最小均方算法(LMS)。 文章介绍了传统自适应算法在主动噪声控制系统中的局限性。传统的自适应算法主要采用Widrow-Hoff LMS算法,其流行性主要归因于其计算复杂度低和对实现错误的鲁棒性强。Widrow-Hoff LMS算法的目标是通过调整控制滤波器的权重来最小化输出误差。然而,当参考信号的自相关矩阵的特征值分布广泛时,LMS算法产生的过剩均方误差主要取决于自相关矩阵的条件数。 为了解决这一问题,文章提出了两种基于小波的自适应算法,分别是分解最小均方算法(D-LMS)和分解重建最小均方算法(DR-LMS)。这两种算法被应用于包括磁流变弹性体(MRE)在内的噪声控制系统。MRE是一种智能粘弹性材料,其复杂的模量取决于振动频率,并且可以通过外部磁场进行控制。 文章通过模拟结果表明,基于小波的D-LMS和DR-LMS算法能够显著提高MRE控制系统的降噪性能,相比于传统的LMS算法。这一发现对于主动噪声控制系统的性能提升具有重要意义。 文章的主要知识点包括: 1. 主动噪声控制(ANC)系统:ANC系统是一种用于减少或消除不需要的声音或噪声的技术,通常用于减少机械设备的噪声或者改善声学环境。 2. 自适应算法:自适应算法是一种能够根据环境变化自动调整其参数的算法,广泛应用于信号处理、控制系统等领域。 3. 小波变换:小波变换是一种用于分析信号的数学方法,它能够将信号分解为一系列在时间-频率平面上具有特定形状和大小的“小波”。这种方法在信号去噪、数据压缩等领域有着广泛的应用。 4. 磁流变弹性体(MRE):MRE是一种新型智能材料,其力学性能可以通过外部磁场进行调节。这种材料在机械工程、汽车工业等领域有着广泛的应用前景。 5. Widrow-Hoff LMS算法:这是一种广泛应用于自适应滤波器设计的算法,其主要目标是通过调整滤波器的权重来最小化输出误差。 6. 分解最小均方算法(D-LMS)和分解重建最小均方算法(DR-LMS):这两种算法是基于小波变换的自适应算法,主要用于提高噪声控制系统的性能。通过模拟实验,这两种算法被证明能够显著提高MRE控制系统的降噪性能。 通过这篇文章,我们可以了解到小波自适应算法在噪声控制系统中的应用前景,以及小波变换在信号处理领域的重要作用。同时,文章也为进一步研究如何提高噪声控制系统的性能提供了新的思路和方法。

剩余8页未读,继续阅读

- 粉丝: 3
- 资源: 970
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- deepseek 与 ChatGPT 的比较.pdf
- 开关电源变压器设计-卢经纬.pdf
- DeepSeek-VL2:用于高级多模态理解的专家混合视觉语言模型.pdf
- DeepSeek 提示词编写技巧.pdf
- MAME模拟器二进制软件
- DeepSeek的启示:地方如何培育创新.pdf
- DeepSeek官方服务器无法使用的替代方案指南.pdf
- DeepSeek常用高级指令 -60个 保姆级指令.pdf
- Deepseek满血版私用部署手把手教程.pdf
- DeepSeek强势崛起:AI创新狂潮下的安全警钟.pdf
- DeepSeek如何赋能职场应用?——从提示语技巧到多场景应用.pdf
- deepseek私域部署指南 -应用-接入-部署大全.pdf
- DeepSeek行业级应用白皮书 精准数据洞察与自动化效能提升方法论.pdf
- DeepSeek行业应用案例集:解锁智能变革密码.pdf
- DeepSeek与AI幻觉研究报告.pdf
- 一文读懂MongoDB之单机模式搭建


 信息提交成功
信息提交成功