FlowtransitionsinmodelCzochralskiGaAsmelt(2006年)资源-CSDN文库

自然科学

论文

需积分: 5 140 浏览量 2021-04-23 07:19:16 上传评论收藏 267KB PDF 举报

资源推荐

资源详情

资源评论

J Chongqing Univ.-Eng. Ed.

Mechanical & Electrical Engineering

Vol. 5 No. 2

June 2006

Article ID: 1671-8224(2006)02- 0063-08

Flow transitions in model Czochralski GaAs melt

∗

CHEN Shu-xian

1,a

, LI Ming-wei

1,2

Institute of Power Engineering of Chongqing University, Chongqing 400030, P. R. China

Second-Term National 985 Project within Research Center of Biological Function Information and Instruments of

Chongqing University, Chongqing 400030, P. R. China

Received 7 December 2005; revised 24 March 2006

Abstract: The flow and heat transfer of molten GaAs during Czochralski growth are studied with a time-dependent and three-

dimensional turbulent flow model. A transition from axisymmetric flow to non-axisymmetric flow and then back to axisymmetric

flow again with increasing the crucible rotation rate is predicted. In the non-axisymmetric regime, the thermal wave induced by the

combination of coriolis force, buoyancy and viscous force in the GaAs melt is predicted for the first time. The thermal wave is

confirmed to be baroclinic thermal wave. The origin of the transition to non-axisymmetric flow is baroclinic instability. The critical

parameters for the transitions are presented, which are quantitatively in agreement with Fein and Preffer’s experimental results.

The calculated results can be taken as a reference for the growth of GaAs single-crystal of high quality.

Keywords: Flow transitions; thermal wave; baroclinic instability; GaAs melt

CLC number: TF061.23 Document code: A

1 Introduction

The Czochralski (CZ) technique is the most common

technique to grow single crystals. It has been pointed

out by several researchers (e.g. Ref. [1]) that melt flow

in the crucible plays an important role on the quality of

the crystals in terms of impurity and grain orientation.

The melt convection during crystal growth represents a

balance among many competing driving forces: viscous

damping, buoyancy, centrifugal, and Coriolis forces.

Small changes in these competing driving forces have

been observed to have a dramatic effect on the melt

flow patterns. So, understanding the flow transitions

and associated instabilities in the Czochralski system is

of great importance.

In the past 20 years, there have been many works

(e.g. Ref. [2] and references cited therein) that have

dealt with flow transitions and instabilities in the

Czochralski crystal growth system. Most of these

results were however obtained for the high Prandtl (Pr)

number melt such as Gd

and Bi

SiO

. There

are few reports on the melt flow transitions and

instabilities for low Prandtl (Pr) number melt such as Si

and GaAs. Especially for GaAs, only Polezhaev, et al.

[3] studied the convective interaction and instabilities

in the CZ GaAs melt. But they used the laminar model

CHEN Shu-xian(陈淑仙): Female; Born 1975; PhD candidate;

Research interest: energy, momentum and mass transfer in CZ

crystal growth; E-mail: bellesavana@163.com

Supported by the Natural Science Foundation of China (No

50376078).

to simulated the melt flow which gets further into the

turbulent regime with Grashof and Rayleigh numbers

beyond 10

[4], and only discussed the origin of the

pure buoyant convective instability without capturing

the flow transition characteristic and its instability

under the complex interaction of viscous damping,

buoyancy, centrifugal, and Coriolis forces.

In the present investigation, a time-dependent and

three-dimensional numerical simulation of the flow and

heat transfer in the CZ GaAs melt with a rotating

crucible is performed, aiming at a fundamental

understanding of the flow transitions and their

associated instabilities, determination of the reason and

the parameter for the onset of these transitions and the

possibilities of damping them. The comparison with the

available results is done.

2 Physical and mathematical model

2.1 Physical model

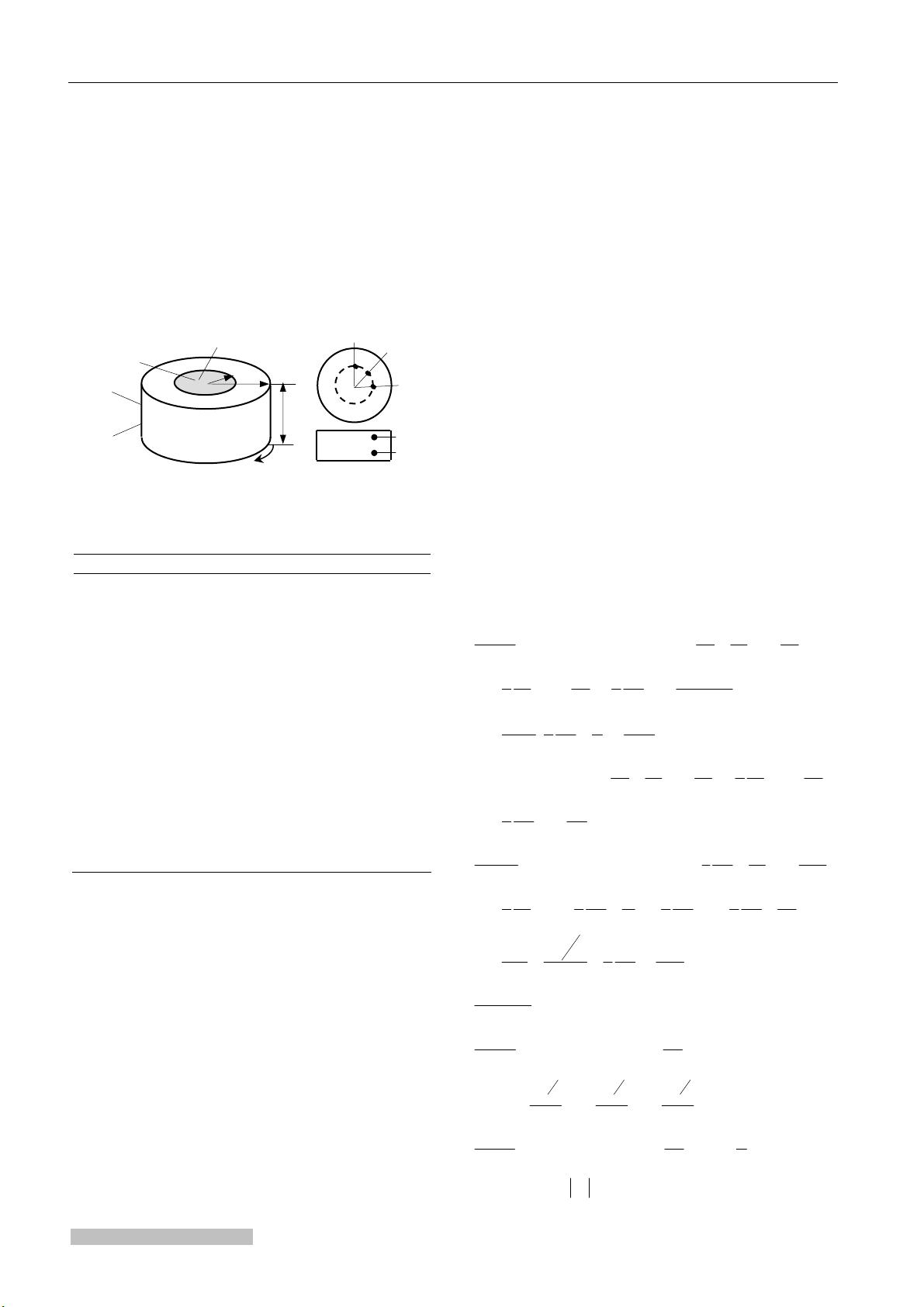
Schematic diagram adopted in the present simulation

is shown in Fig.1. The crucible contains GaAs melt

with height H and radius R

. The crystal, represented

by a copper disc, has a constant radius R

. The crucible

rotates at an angular velocity Ω

in the clockwise

direction from a top view, whereas the crystal is

standing still. The melt/crystal interface is assumed flat

with the melting temperature T

. The bottom wall of

the crucible is adiabatic and the inside wall of the

crucible is at a fixed temperature of T

= 1 521 K. The

free surface is assumed to be plane and has a radiate

J Chongqing Univ.-Eng. Ed.

Mechanical & Electrical Engineering

Vol. 5 No. 2

heat exchange with the ambient environment with a

temperature of T

= 1 512 K. The Marangoni force at

the free surface is taken into account. No-slip boundary

conditions are applied on all the rigid boundaries. As

the initial conditions for the melt, zero velocity

components and a homogeneous temperature

distribution with T

init

=0.5 (T

+ T

) are assigned. The

thermo-physical properties of GaAs melt and the

processing parameters used here are given in Table 1.

Fig.1. Schematic illustration of the calculating model for the

melt in (a) the CZ crystal growth configuration; and (b) the

arrangement of monitors.

Table 1 Physical properties and processing parameters

Parameter Symbol Value Unit

Density ρ 572 0 kg/m

Dynamic viscosity μ 0.002 79 kg /m s

Kinematic viscosity ν 4.878×10

−7

Thermal conductivity λ 17.8 W/m K

Specific heat c

434 J/kg K

Emissivity ε

0.3

Thermal diffusivity α 7.17×10

−6

Melting temperature T

1511 K

Coefficient of thermal

expansion

β 0.000 187 K

−1

surface tension

temperature coefficient

−1.2×10

−3

N/m K

Crucible radius R

0.075 m

Crystal radius R

0.037 5 m

melt height H 0.06 m

Crucible rotation rate Ω

0 to 16 r/min

To detect thermal waves, at two vertical positions

z=0.018 5 m and z= 0.048 5 m indicated by indices of b

and d in Fig. 1b, three monitor points are located at the

same radial position r=0.038, and they are separated

azimuthally by Φ=π/4 in the clockwise direction as

shown in Fig. 1b. The melt flow in the convection cell

is characterized by the Grashof number (Gr =

gβH

ΔT/ν

), rotational Reynolds number (Re

= Ω

/ν), Marangoni number (Ma = γ

ΔT(R

-R

)/ρν

), thermal

Rossby number (Ro

= gβHΔT /4Ω

) and Taylor

number (Ta = 4Ω

/ν

H), where β is the volumetric

thermal expansion coefficient of GaAs melt, g the

gravitational acceleration, γ

the surface tension

temperature coefficient,

ΔT the driving temperature

difference between the disk wall and the side-wall of

the crucible, Ω

the rotational rate of the crucible, and ν

the kinematic viscosity. The calculation is carried out

in the following parameter ranges: Gr=1.665×10

Ma=3.306×10

, Ω

=0 to 16 r/min, Re

=0-1.545 7×10

=∞-0.017 43, Ta=0-1.866 5×10

2.2 Mathematical model

Because the Grashof number Gr is of the order of

, so the flow in the melt is turbulent [4]. The flow

and heat transfer in the melt are governed by the three-

dimensional Reynolds-averaged equations for an

incompressible melt expressing the conservation of

mass, momentum and energy. Buoyancy is taken into

account by the Boussinesq approximation. The

Reynolds stress tensor in the Reynolds-average

equations of motion is described using the k-ε model

formulation. In the well-known family of k-ε models,

the low-Reynolds number k-ε model is proved to be the

most successful in describing the melt and near-wall

flow [5]. So the low-Reynolds number k-ε model

proposed by Jones and Launder is used here. In a

cylindrical coordinate system centered at the bottom of

the crucible, the governing equations and the

constitutive relationship can be written as follows:

∇

⋅= (1)

eff eff

() v

() ( ) ( )

11(/)

( ) [ ]

Vu u

trzr

urwr

rr r r r

ρμ μ

μμ

∂∂∂∂

∇⋅ =∇⋅ ∇ − + +

∂∂∂∂

∂∂ ∂∂

+−

∂∂∂ ∂

eff

( )

wu w

rr r r

∂

(2)

eff eff eff

)( ) ( ) ( )

pv u

Vv v r

zzrr z

ρμ μ μ

∂

∂∂ ∂ ∂

∇⋅ ∇ − + + +

∂∂ ∂ ∂ ∂

eff ref

( ) ( )

μρβ

∂

−−

∂∂

(3)

eff eff

() 1

() ( ) ( )

11 112

[ ( )] [ ( )]

wpv

Vw w

tzr

uw w u

rr r r r r r

ρμ μ

θθ

μμ

θθθ

∂∂∂∂

∇⋅ =∇⋅ ∇ − + +

∂∂∂∂

∂∂ ∂∂

−+ + +

∂∂ ∂∂

eff

()

[ ]

vuv

rrr r

∂

+−

∂∂

(4)

eff

()

()()

Vc T k T

∂

∇⋅ =∇⋅ ∇

∂

(5)

()

() [( )]

Vk k G G

μρε

∂

∇⋅ =∇⋅ + ∇ + + − −

∂

111

222

2[()()()]

kkk

rzr

∂∂∂

(6)

()

() [( ))][

VcfG

εε

ρε μ ε

∂

∇⋅ =∇⋅ + ∇ + −

∂

122

]

cG c f

εε

−

(7)

(b)

(a)

Inside wall

of crucible

stal

Ω

剩余7页未读，继续阅读

评论收藏

内容反馈

weixin_38503233

粉丝: 9
资源: 918

Flow transitions in model Czochralski GaAs melt (2006年)

最新资源

Flow transitions in model Czochralski GaAs melt (2006年)

Phase transitions in information spreading on structured populations 翻译

Magnetoabsorption spectra of magnetoexciton transitions in GaAs/Ga0.7Al0.3As quantum wells

Python有限状态机——transitions

spring webflow 官方中文版权威指南PDF

Simulink的Stateflow教程

Transitions and Animations in CSS3

Transitions and Animations in CSS mobi

前端开源库-glsl-transitions

Transitions Plus v4.0

spring web flow 官方文档

Stateflow教程.pdf

Possibility of superradiant phase transitions in coupled two-level atoms

spring web flow权威指南

spring webflow的一个例子

0-π transitions in mesoscopic Josephson junctions with magnetic impurity interlayers

spring-webflow-reference.pdf

Android代码-Transitions-Everywhere

Transitions-150组视频转场动画

spring-webflow-2.3.1官方jar包

UI专用的特效插件-Beautiful Transitions 新版本

webflow2.42 jar包

spring web flow入门demo

stateflow教程

spring webflow

spring web flow 小项目

基于MATLAB/SIMULINK的并网型双馈风力发电机仿真模型的研究 (2010年)

BUCK/BOOST转换器小信号建模与稳定性分析 (2009年)

最新资源