没有合适的资源?快使用搜索试试~ 我知道了~
资源推荐
资源详情
资源评论

高 校 毕 业 生 就 业 竞 争 力 分析
倡
杨春华, 杨 玲
(保山师范高等专科学校,云南 保山 678000)
摘 要: 根据 2009 年严峻的就业形势和历年高校毕业生就业情况,基于全国高校毕业生就业状况大
规模抽样调查数据。 建立综合、科学而全面的高校毕业生就业竞争力评价体系。 采用数理统计中的回
归分析,分析影响高校毕业生就业竞争力的种种因素,以便学生、高校、社会更好的提高毕业生的就业竞
争力,以便解决当前严峻的就业形势。
关键词: 竞争力;评价体系;回归分析;对策
中图分类号: O212畅1 文献标识码: A 文章编号: 1007 -9793(2009)05 -0039 -07
自上世纪末本世纪初高校大规模扩招和毕业生就业模式改革以来,由于种种原因,高校毕业生就业
难的问题日渐突出突出。 据教育部统计,除去 10%考研、考博学生、专升本学生以及出国留学学生,再
加上去年待就业的 70 万 ~90 万人,今年实际需要就业的人数约在 611 万人左右。 从往年高校毕业生
就业率情况来看,即使不发生全球性金融危机也是很难解决这么多人就业问题的,更何况我们还处在全
球金融危机的阴影下。 更为严重的是,综合各方面的信息来看,高校毕业生就业难的问题未来比较长的
一个时期内很难得到根本性的解决。
这一形势不仅向在校大学生而且也向各高校提出了应该怎样提高就业竞争力的挑战? 要更好地迎接
这个挑战,我们首先必须首先解决究竟哪些因素影响毕业生就业竞争力的问题。 国内不少学者就这个问
题作了许多有成效的探索与研究,岳昌君等
[3]
的研究指出:内因对毕业生就业竞争力影响显著大于外部因
素;罗昌勤
[9]
用因子分析法分析了就业竞争力的 8 个影响因子,发现能力因子和交际因子的影响最为突
出;岳昌君等
[10]
进一步指出:影响高校毕业生就业的因素还包括就业市场、专业结构以及就业观念等等。
这些工作用不同的方法,从不同的角度探讨了影响毕业生就业竞争力问题,为我们更深入地探索这个问题
奠定了良好的基础。 本文利用调查数据,用 Logistic 模型建立了高校毕业生就业竞争力影响因素模型,并
以模型结论为基础提出了一些学生个人、学校和社会三方面提高就业竞争力的对策建议。
1 高校毕业生就业竞争力评价体系
毕业生就业受多种因素的影响,各种因素的相对重要性又如何? 应该从社会、学校和学生三种角度
综合考虑,本文只讨论学校和学生自身因素。 根据北京大学“高等教育规模扩展与劳动力市场”课题组
的三次对全国高校毕业生的就业状况进行了大规模调查的就业影响因素的归纳总结和实际情况建立以
下的毕业生就业竞争力评价体系(简称就业竞争力评价体系)。 (见图 1)
2 高校毕业生就业竞争力模型
我们希望根据调查数据找出就业竞争力评价体系中的三级指标对毕业生就业竞争力(简称就业竞
第 29 卷第 5 期
2009 年 9 月
云南师范大学学报
Journal of Yunnan Normal University
Vol.29 No.5
Sep.2009
倡
收稿日期:2009 -04 -24
作者简介:杨春华(1973 -),男,云南省施甸县人,讲师,在职硕士,主要从事最优化理论及其应用方向研究 畅
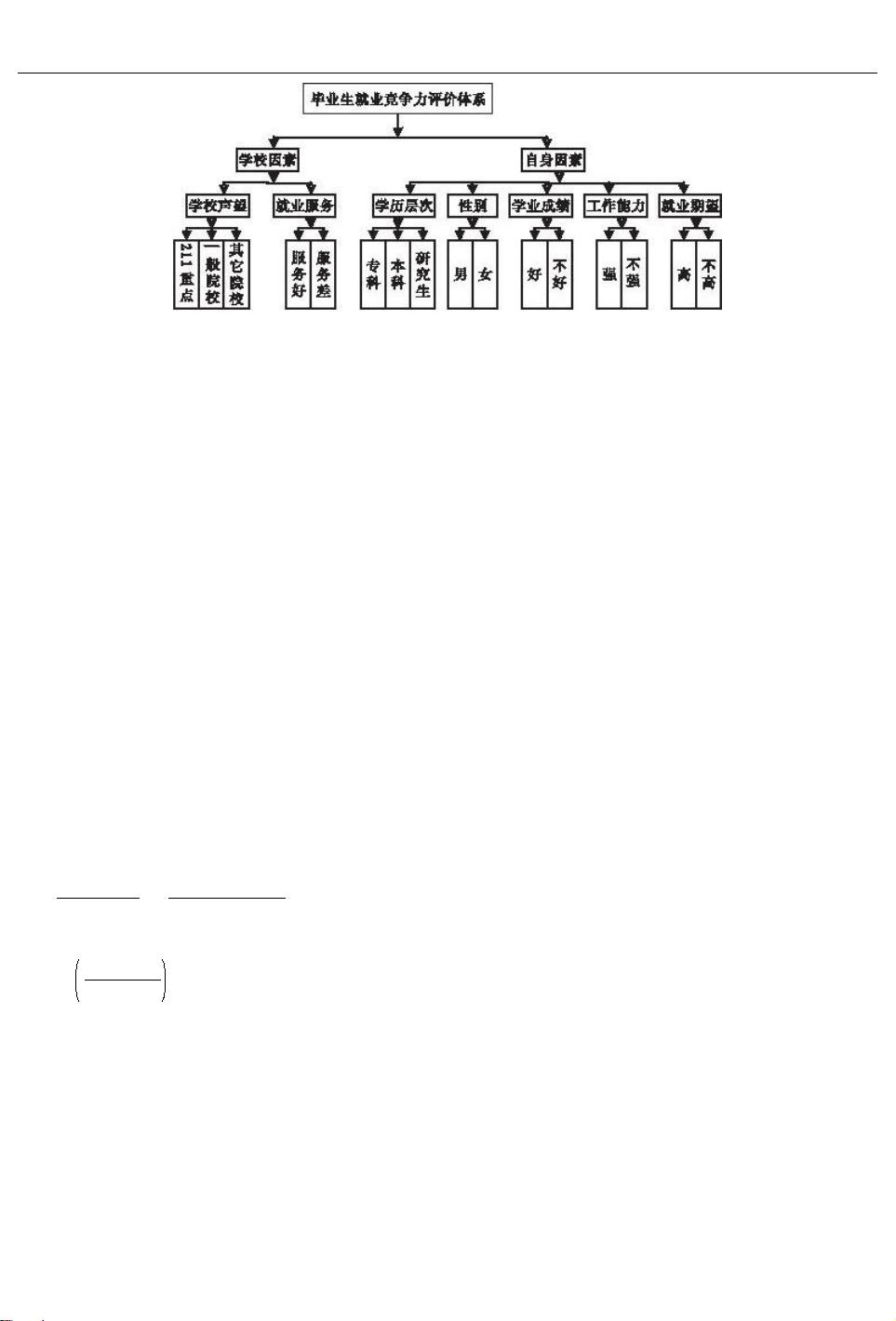
图 1 毕业生就业竞争力评价体系
Fig畅1 Graduates'Employment Competition Evaluation System
争力)的影响方式,即找出就业竞争力关于学校声望、就业服务、学历层次、性别、学业成绩、工作能力、
就业期望的某种函数关系。
由于毕业生的就业情况只有成功与失败两种,因此,我们可以用一个二值随机变量来描述就业情
况。 在给定影响因素取值的条件下,如果一位毕业生就业竞争力高,那么,他成功就业的概率就大,否
则,他成功就业的概率就小,因此,我们可以用在给定影响因素取值的条件下成功就业的概率来衡量就
业竞争力。 这个特性与 Logistic 模型的特点吻合,因此,后面我们用 Logistic 模型来建立就业竞争力模
型。
2畅1 Logistic 模型
Logistic 模型常用于分析若干影响因素对二值被解释变量的影响,其一般形式为:
被解释变量(随机变量) Y 服从二点分布,其中,Y 的取值定义为:当我们关心的随机事件 A 发生时,
Y =1,否则 Y =0。
解释变量(即影响试验结果的因素) 组为 X =(X
1
,X
2
,……,X
P
)。
假设:在给定 X 的条件下,事件 A 发生(Y =1) 的概率 p(X) 是关于 X 的如下函数:
p(X) =P(Y =1 |X) =e
β
0
+β
1
x
1
+……β
p
x
p
厕(1 +e
β
0
+β
1
x
1
+……β
p
x
p
(1)
根据假设,在给定 X 的条件下,事件 A 不发生(Y =0) 的概率为:
P(Y =0 |X) =1 -P(Y =1 |X) =1 -p(X) =(1 +e
β
0
+β
1
x
1
+……β
p
x
p
)
-1
因此,在给定 X 的条件下,事件 A 发生(Y =1) 的概率与事件 A 不发生(Y =0) 的概率之比为:
p(X)
1 -P(X)
=
P(Y =1 |X)
P(Y =0 |X)
=e
β
0
+β
1
x
1
+……β
p
x
p
上式两边取对数并加上常数项和扰动项,就得到 Logistic 模型的对数回归方程:
In
p(X)
1 -p(X)
=α+∑
p
i =1
β
i
X
i
+ε
其中,回归子 X
i
的系数 β
i
的意义为:若 β
i
>0,则 X
j
的影响为正;否则,X
i
的影响为负。
Logistic 模型的参数估计方法是极大似然估计,似然函数为:
ln L =∑
N
i =1
[y
i
(β
0
+β
1
x
i1
+……β
p
x
ip
) -ln(1 +exp(β
0
+β
1
x
i1
+……β
p
x
ip
))]
Logistic 模型的检验:同普通的线性回归一样,对回归系数 β
i
的估计值 β
^
i
进行显著性检验,通常用
Wald 检验,其公式为:W =β
^
i
厕D(β
^
i
)。其中 D(β
^
i
) 为回归系数 β
i
的估计值 β
^
i
的标准差。如果 β
i
的估计
值 β
^
i
Wald 检验显著,则表示自变量对因变量影响显著,否则影响不显著。
2畅2 就业竞争力影响力模型的设定
根据本节开始的分析和 Logistic 模型的特点,我们设定模型变量为:
被解释变量:毕业生的就业情况,用二值随机变量 Y 来描述,其取值定义为:如果就业成功,则 Y =
1;否则 Y =0。
·04·
云南师范大学学报(自然科学版) 第 29 卷
剩余6页未读,继续阅读
资源评论

weixin_38502762
- 粉丝: 0
- 资源: 925
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功

