稀有衰减π0→e+e-：超出超前阶的校正资源-CSDN文库

Open

Access

135 浏览量 2020-04-02 01:03:54 上传评论收藏 727KB PDF 举报

资源推荐

资源详情

资源评论

Eur. Phys. J. C (2014) 74:3010

DOI 10.1140/epjc/s10052-014-3010-4

Regular Article - Theoretical Physics

Rare decay π

→ e

−

: on corrections beyond the leading order

Tomáš Husek

, Karol Kampf

,Jiˇrí Novotný

Faculty of Mathematics and Physics, Institute of Particle and Nuclear Physics, Charles University, V Holešoviˇckách 2, Praha 8, Czech Republic

Received: 29 May 2014 / Accepted: 25 July 2014 / Published online: 20 August 2014

Abstract The preceding experimental and theoretical

results on the rare decay π

→ e

−

are brieﬂy summarized.

Already computed two-loop QED corrections are reviewed

and the bremsstrahlung contribution beyond the soft-photon

approximation is analytically calculated. The possible fur-

ther contribution of QCD loop corrections is estimated using

the leading logarithm approximation. The complete result

can be used to ﬁt the value of the contact interaction cou-

pling χ

(r)

to the recent KTeV experiment with the result

(r)

) = 4.5 ± 1.0.

1 Motivation

Experimental measurements of the rare decay of a neutral

pseudoscalar meson to a lepton pair and comparison with

theoretical predictions offer an interesting way to study low-

energy (long-distance) dynamics in the Standard Model (SM)

[1–3]. Systematical theoretical treatment of the process dates

back to 1959, when the ﬁrst prediction of the decay rate was

published by Drell [4]. While the possible contributions of the

weak sector of the SM are small enough to be neglected, the

leading order QED contribution is described by two virtual

photon exchange triangle diagram. That is why t he double

off-shell pion transition form factor F

∗

, which is not

known from the ﬁrst principles, plays an essential role.

Because of this one-loop structure for the leading order,

the process is very rare and suppressed in t he comparison to

two-photon decay (π

→ γγ) by a factor of 2(αm

)

due to the approximate helicity conservation of the inter-

action and thus may be sensitive to possible effects of the

physics beyond the SM (the expected branching ratio from

the pure SM calculation is about 10

−7

e-mail: husek@ipnp.mff.cuni.cz

e-mail: karol.kampf@mff.cuni.cz

e-mail: jiri.novotny@mff.cuni.cz

Recently, this decay has attracted the attention of theorists

again in connection with a new precise branching ratio mea-

surement. The KTeV-E799-II experiment at Fermilab [5] has

observed π

→ e

−

events (altogether 794 candidates),

where K

→ 3π

decay was used as a source of neutral

pions. The KTeV result is

(π

→ e

−

, x > 0.95)

(π

→ e

−

γ, x > 0.232)

= (1.685 ± 0.064 ± 0.027) × 10

−4

. (1)

Here we have introduced the Dalitz variable

x ≡

( p + q)

(P − k)

= 1 −

, (2)

where p, q, and k are four-momenta of electron, positron, and

photon, respectively, P = ( p+q +k) is the four-momentum

of neutral pion π

with a mass M and E

is the energy of the

real outgoing photon in the pion CMS. The lower bound of

the Dalitz variable x is used to suppress the contribution of

the Dalitz decay π

→ e

−

γ , which naturally arises with

lower x.

By means of extrapolating the Dalitz branching ratio in

(1) to the full range of x, the branching ratio of the neutral

pion decay into an electron–positron pair was determined to

be equal to

B(π

→ e

−

(γ ), x > 0.95)

= (6.44 ± 0.25 ± 0.22) × 10

−8

. (3)

Here the ﬁrst error is from data statistics alone and the second

is the total systematic error. For the matter of interest, current

PDG average value (6.46 ±0.33) ×10

−8

[6] is mainly based

on this new result.

The KTeV Collaboration used the result (3) for further

calculations. They used the early calculation of Bergström [7 ]

to extrapolate the full radiative tail beyond x > 0.95 and to

scale the result back up by the overall radiative corrections of

123

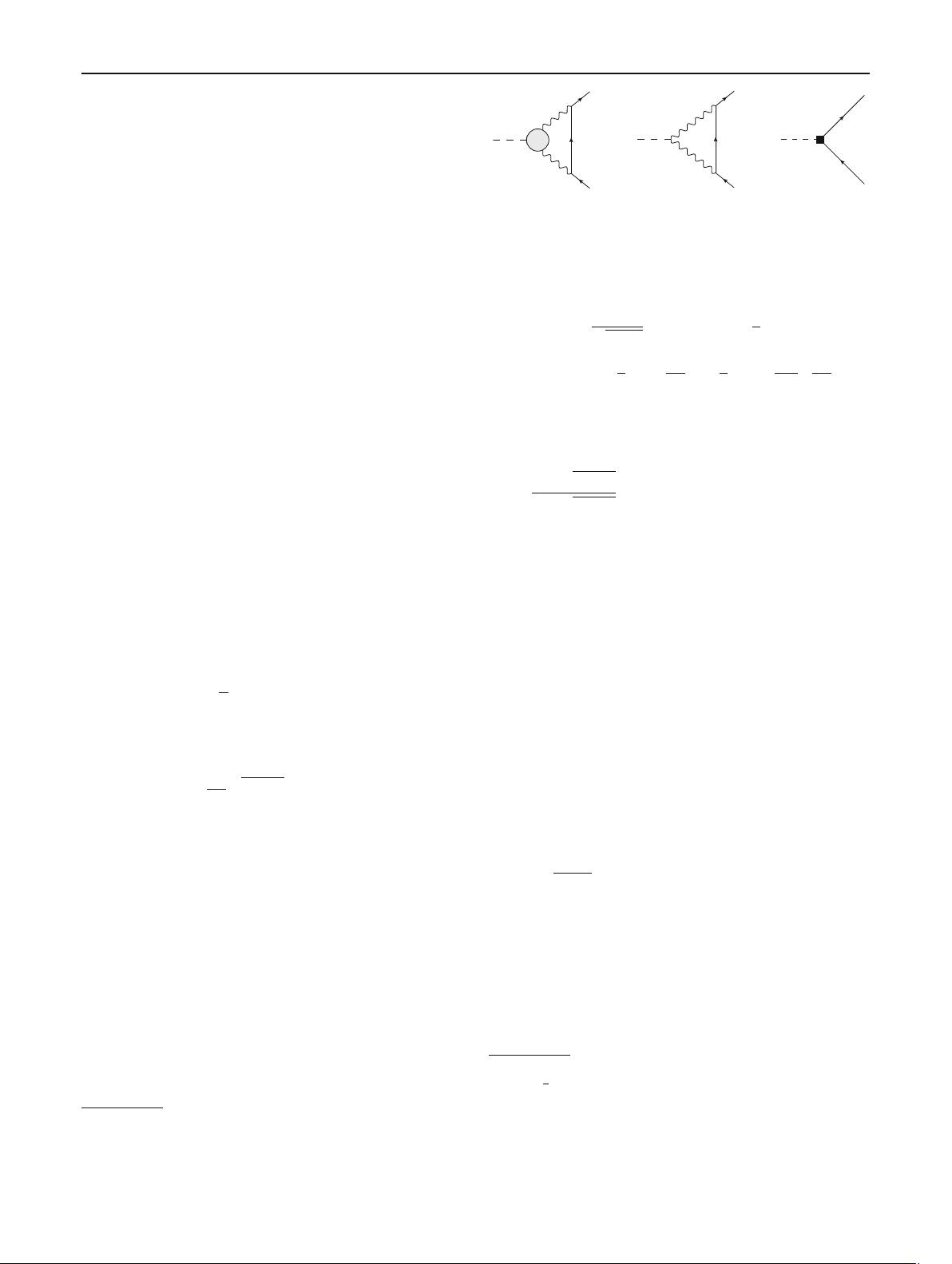
3010 Page 2 of 11 Eur. Phys. J. C (2014) 74:3010

3.4 % to get the lowest order rate (with the ﬁnal state radiation

removed) for π

→ e

−

process. The ﬁnal result is

no-rad

KTeV

(π

→ e

−

) = (7.48 ± 0.29 ± 0.25) × 10

−8

(4)

Subsequent comparison with theoretical predictions of the

SM was made in [1,2] using pion transition form-factor data

from CELLO [8] and CLEO [9] experiments. Finally, it has

been found that according to the SM the result should be

no-rad

(π

→ e

−

) = (6.23 ± 0.09) × 10

−8

. (5)

This can be interpreted as a 3.3 σ discrepancy between

the theory and the experiment. Of course, the discrep-

ancy initiated further theoretical investigation of its possible

sources [10,11]. Aside from the attempts to ﬁnd the corre-

sponding mechanism within the physics beyond the SM, also

the possible revision of the SM predictions has been taken

into account. Many corrections of this kind have been already

made, but so far with no such a signiﬁcant inﬂuence on the

ﬁnal result.

2 Leading order

According to the Lorentz symmetry the on-shell invariant

matrix element of the π

→ e

−

process can be generally

written in terms of just one pseudoscalar form factor

iM(π

→ e

−

) = u( p, m)γ

v(q, m)P(p

, q

, P

) (6)

and, as a consequence, the total decay rate is given by

(π

→ e

−

) =

8π



1 − ν



P(m

, m

, M

)



, (7)

where m stands for electron mass and ν ≡ 2m/M. The lead-

ing order in the QED expansion is depicted as the left hand

side of the graphical equation in Fig. 1. Here the shaded

blob corresponds to the off-shell pion transition form factor

∗

,(P − l)

) where l is the loop momentum. This

form factor serves as an effective UV cut-off due to its 1/l

asymptotics governed by OPE (see e.g. [12]) and the loop

integral over d

l is therefore convergent. It is convenient to

pick up explicitly the non-analytic contribution of the two-

photon intermediate state (the imaginary part

is determined

uniquely up to the normalization given by the on-shell value

of F

∗

(0, 0) ≡ F

γγ

) and express the form factor in

the following way (cf. [13]):

Imaginary part of this contribution is given by Cutkosky rules cutting

the two virtual photon lines in the Fig. 1.

Fig. 1 Leading order contribution in the QED expansion and its repre-

sentation in terms of the leading order of the chiral perturbation theory

, m

, M

)

= α

γγ

√

1−ν



(z) − Li





+iπ log(−z)



+2α

γγ



log





−

+ χ





(8)

Here, Li

is the dilogarithm,

z =−

1 −

√

1 − ν

1 +

√

1 − ν

, (9)

and μ represents the intrinsic scale connected with the form

factor

∗

. The function χ(P

/μ

, m

/μ

) represents

the remainder which collects the contributions of higher

intermediate states and is real and analytic

for P

/μ

< 1.

The leading order terms in the chiral expansion of the

form factor P

are depicted as the right hand side of the

graphical equation in Fig. 1.Theπ

γγ vertex in the loop

graph is local and corresponds to the leading order term of

the chiral expansion of the form factor F

∗

. Therefore

the loop integration is no more UV ﬁnite and a countert-

erm (represented by the tree graph in Fig. 1) is necessary.

The sum of these two terms can be written in the form (8),

where the transition form factor F

γγ

and the remainder

χ(P

/μ

, m

/μ

) are replaced by their leading orders in

the chiral expansion,

γγ

4π

,χ

/μ

, m

/μ

) = χ

(r)

(μ), (10)

where χ

(r)

(μ) is the ﬁnite part of the above mentioned coun-

terterm renormalized at scale μ. The graphical equation in

Fig. 1 can be understood as the matching condition for

(r)

(μ) at the leading order in the chiral expansion. It enables

one to determine χ

(r)

(μ) once the form factor F

∗

known. The latter can be theoretically modeled e.g. by the

It means the scale at which the loop integral is effectively cut off.

The term

log(m

/μ

) represents the leading dependence of the form

factor P on this scale.

Note that the higher intermediate states, which appear when also the

blob in Fig. 1 is cut, start for P

∼ μ

123

剩余10页未读，继续阅读

评论收藏

内容反馈

weixin_38502722

粉丝: 5
资源: 926

稀有衰减π0→e + e-：超出超前阶的校正

最新资源

稀有衰减π0→e + e-：超出超前阶的校正

衰减D0→K-π+ e + e-的观察

研究稀有Bs0和B 0衰减到π+π-μ+μ-最终状态

Z→π+ π−，K + K−：微扰QCD方法的试金石

涉及c→ul + l-（li∓lj±）跃迁的魅力介子衰变中的新物理效应

相对论夸克模型中的稀有$$ \ Lambda _c \ rightarrow p \ ell ^ + \ ell ^-$$Λc→pℓ+ℓ-衰减

搜索过程e + e-→η

衰减μ→ee + e-νν¯$$ \ mu \至e \ kern0.22em \ left（{e} ^ {+} {e} ^ {-} \ right）的次要阶数预测 \; \ nu \ kern0.2em \ overline {\ nu} $$

通过WASA-at-COSY搜索在衰变中的违规行为→

通过使用角度不对称性探索B→Dℓ+ℓ-衰变中的新物理学

对齐的两希格斯-双重峰模型中的Λb→Λ（→pπ-）μ+μ-衰减

近似物理介子质量的稀有钾衰变K +→π+νν¯的格子QCD研究

在B→K ** ++-衰变中建立轻子风味普遍性违规

相对论夸克模型中的稀有B→πll和B→ρll衰减

搜索衰减Ds +→γe+νe

B包含性稀有B衰变和B现象的远距离效应$$ \ overline {B} $$→X dℓ+ℓ-

稀有衰变中的魅力散发贡献

Qt 5实现串口调试助手 （源工程文件、0积分下载）

【SystemVerilog】路科验证V2学习笔记（全600页）.pdf

AutoSAR标准协议4.2.2

光伏-储能并网系统仿真.rar

XCP协议的规范文档

GD32替换STM32注意事项.pdf

NPPJSONViewer.zip

蓝牙BLE协议中文版.pdf

CANoe通过CAPL脚本实现自动测试

AD20官方中文教程.pdf

最新资源

Qt 5实现串口调试助手（源工程文件、0积分下载）