受限玻尔兹曼机研究综述1

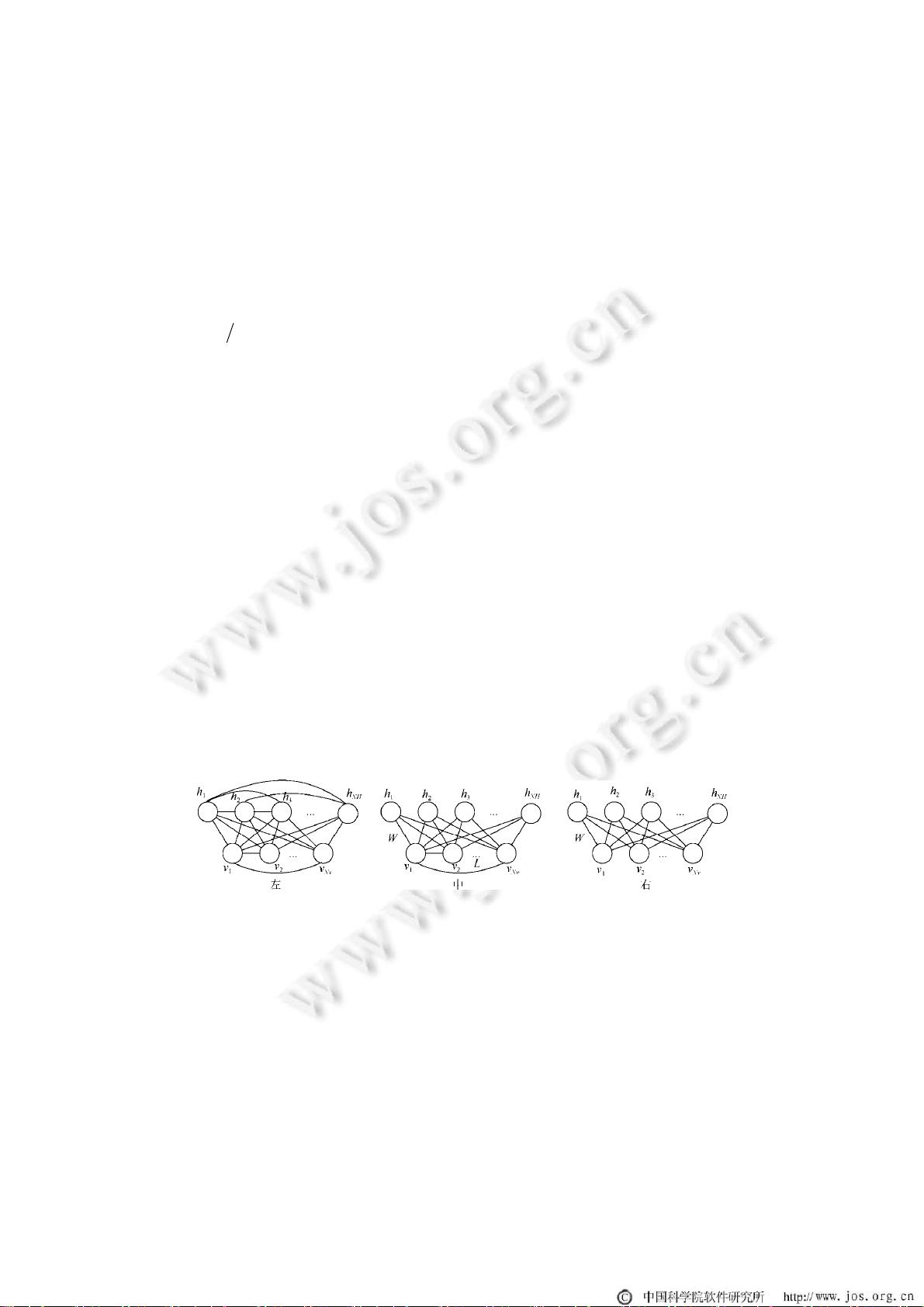
受限玻尔兹曼机（Restricted Boltzmann Machines, 简称RBM）是一种无向概率图模型，它在机器学习领域中占有重要地位，尤其是在深度学习和图像、语音处理等应用中。RBM最初由Geoffrey Hinton等人提出，它的主要特点是能够通过无监督学习来捕获数据的潜在结构。 一、基本概念与训练算法 RBM由两层神经元构成：可见层（Visible layer）和隐藏层（Hidden layer）。可见层神经元通常对应输入数据，而隐藏层神经元则用于学习数据的特征表示。RBM的训练目标是找到一组权重参数，使得模型能够尽可能地复现其训练数据。常用的训练算法包括对比散度（Contrastive Divergence, CD-k）和玻尔兹曼机蒙特卡洛（Boltzmann Machine Monte Carlo, Gibbs Sampling）等。这些算法都是基于最大似然估计，通过迭代更新权重来逼近数据的真实分布。 CD-k算法是一个近似方法，通过k步的马尔可夫链采样来近似真实分布，其中k值的选择对训练效果有很大影响。Gibbs Sampling则是通过模拟系统的热力学演化，达到从模型分布中采样的目的，但其收敛速度较慢。 二、RBM的最新研究进展 近年来，RBM的研究不断深化，引入了新的优化策略和技术。例如，对抗损失（Adversarial Loss）被引入到目标函数中，以增强模型对异常数据的鲁棒性。此外，Wasserstein距离也被用来改进模型的学习过程，使其更加稳健。同时，RBM与变分自编码器（Variational Autoencoders, VAEs）的结合形成了基于RBM先验的变分自编码模型，这种模型能够更好地进行概率分布的建模，生成更为逼真的样本。 三、RBM在深度学习中的应用 RBM作为预训练模型在深度信念网络（Deep Belief Networks, DBNs）中起到了关键作用，通过逐层预训练可以有效地初始化深度网络的权重，从而改善深度网络的训练效率。此外，RBM也被应用于协同过滤推荐系统、自然语言处理、计算机视觉等多个领域。 四、问题与未来研究方向 尽管RBM在许多任务中表现出色，但仍存在一些挑战，如训练复杂度高、收敛速度慢等。未来的研究方向可能包括： 1. 提升训练效率：寻找更有效的优化算法或并行计算策略，以减少训练时间。 2. 结构改进：探索新的网络结构，如深度RBM，以增强模型的表达能力。 3. 结合其他模型：与其他深度学习模型（如卷积神经网络）融合，以提升模型的性能。 4. 理论完善：进一步理解RBM的统计力学性质，以及如何更好地利用其生成和判别能力。 受限玻尔兹曼机作为一种强大的概率图模型，已经并将继续在机器学习和深度学习领域发挥重要作用。随着理论和算法的不断进步，RBM有望在更多领域找到新的应用。