习题 9-31

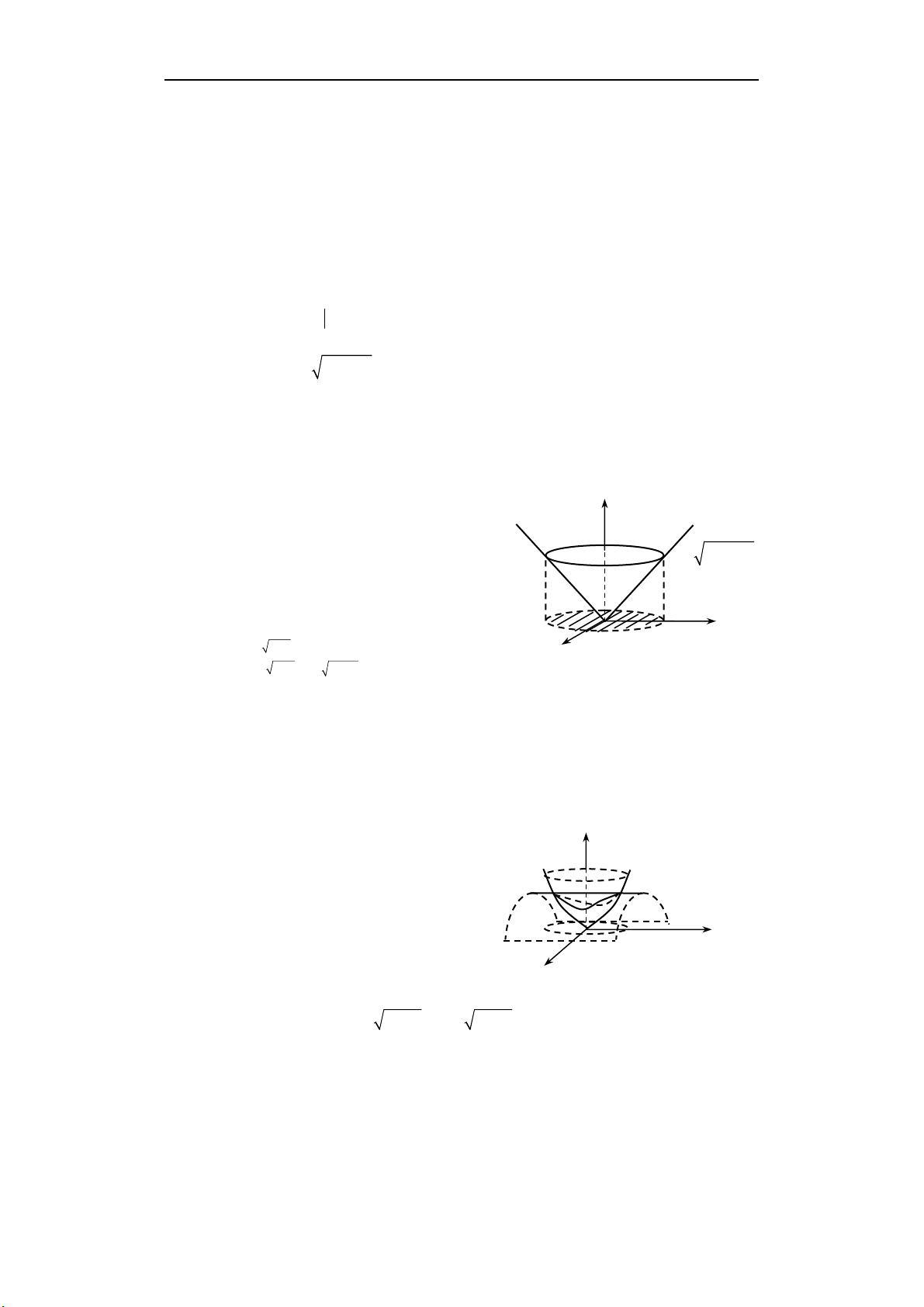
【知识点详解】 三重积分是数学中用于计算三维空间中物体体积、质量、密度等问题的一种积分形式。在直角坐标系中，三重积分通常表示为 ∫∫∫f(x, y, z)dV，其中f(x, y, z)是被积函数，dV代表微元体积。 在习题9-31中，我们需要将三重积分转化为直角坐标系下的三次积分，并计算给定的积分区域的体积。 1. 第一部分：( , , ) 02,13, 02x y zxyzΩ =≤≤≤≤≤≤ 这个积分区域是一个立方体，其边界为x=0, y=0, z=0, x=2, y=2, z=3。因此，三重积分可以表示为： ∫∫∫f(x, y, z)dxdydz，其中积分的上下限分别为x从0到2，y从0到2，z从0到3。 2. 第二部分：由锥面22zxy=+与平面1z = 围成的闭区域 这个区域在xOy平面上的投影是一个半径为1的圆，因此可以先对xOy面上的圆进行积分，然后再对z进行积分。三重积分可以写为： ∫∫∫f(x, y, z)dA dz，其中dA是圆上的元素面积，dz是从1到锥顶的积分。 3. 第三部分：由双曲抛物面 zxy=及平面1xy+= ,0z =围成的闭区域 投影在xOy平面上是两条对角线形成的矩形，然后对z进行积分。三重积分可以表达为： ∫∫∫f(x, y, z)dy dx dz，其中积分的边界是根据x和y的范围来确定的。 4. 第四部分：由曲面222zxy=+及22zx=−围成的闭区域 投影在xOy平面上是两个相交的圆，可以先计算这两个圆在z=0和z=2之间的体积，再相减。三重积分会涉及到两部分的积分。 对于第二部分的解答，我们先在xOy平面上计算圆的面积，然后对z从1到2积分，即： ∫∫[f(x, y, z)|_{z=1}^{z=2}]dA，其中dA是圆上的元素面积。 第三部分的解答中，我们可以看到Ω在xOy平面上的投影由x轴、y轴和直线1xy+=围成，因此： ∫∫[f(x, y, z)|_{z=0}^{z=1}]dy dx，积分区域为0≤x≤1, 0≤y≤1。 第四部分，需要先找出两个圆在z=0和z=2时的交集，然后进行积分，即： ∫∫[f(x, y, z)|_{z=2}^{z=0}]dA - ∫∫[f(x, y, z)|_{z=2}^{z=0}]dA'，其中dA和dA'分别是两个圆的面积元素。 在问题的第二小问中，如果被积函数f(x, y, z)可以分解为f(x) * g(y) * h(z)，那么三重积分可以转化为三个二重积分的乘积。这利用了积分的线性性质和积分次序的可交换性。 第三小问提供了几个具体的三重积分的计算示例，包括不同几何形状的闭区域，需要结合积分的几何意义来确定积分的上下限。 总结来说，解决这类问题的关键在于理解积分区域的几何特性，正确选择积分变量的顺序，并掌握如何将三重积分转化为二维积分或一维积分进行计算。通过这样的转换，我们可以有效地求解三重积分问题，从而得到所求的体积或其他物理量。