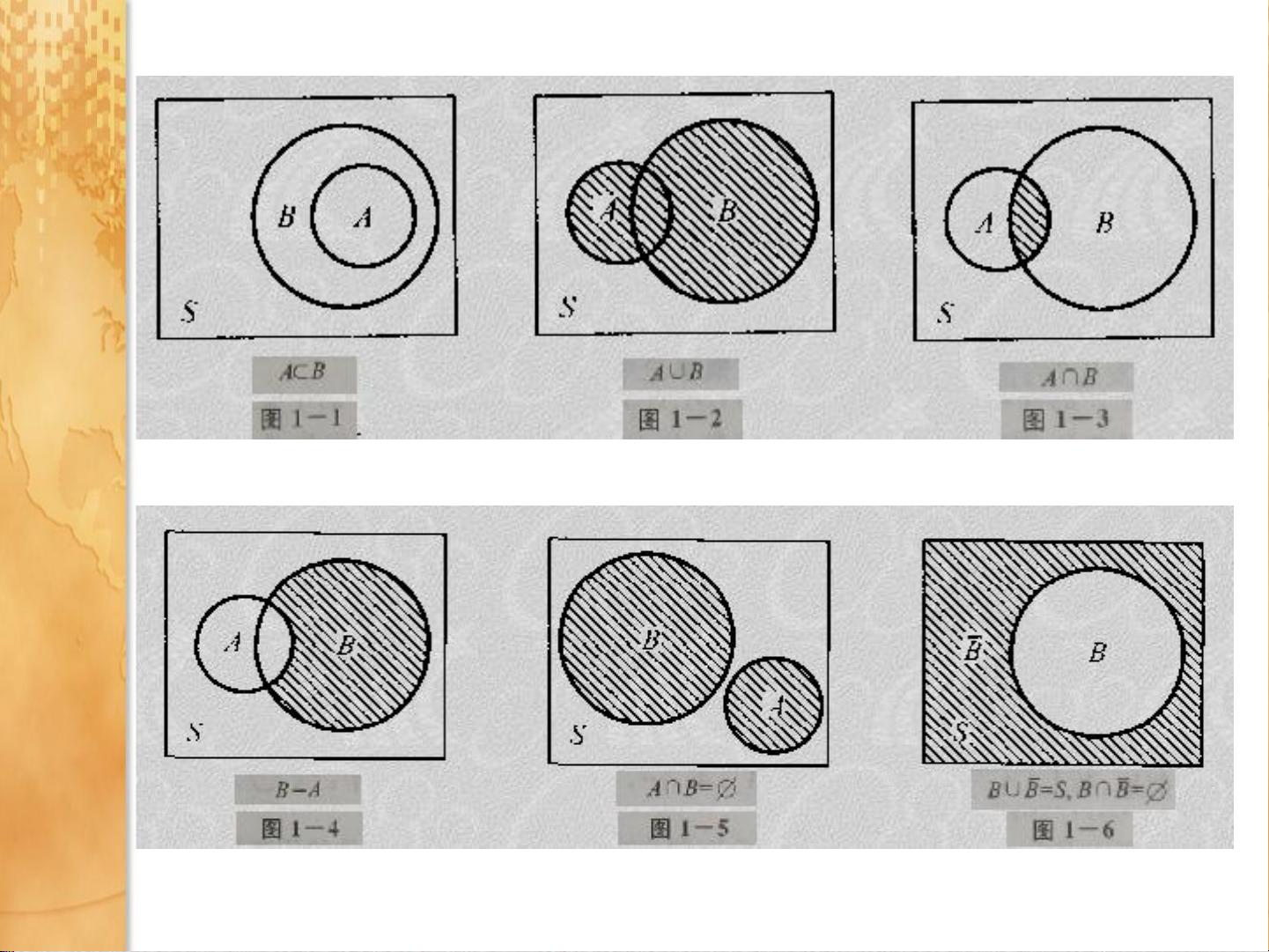
概率论与数理统计总复习3

【概率论与数理统计总复习3】 概率论是一门研究随机现象的数学理论，它主要探讨事件发生的可能性。在本复习中，我们将重点关注事件间的关系及其运算定律，以及概率的定义、性质和计算方法。 1. **事件间的关系** - **包含关系**：事件A发生必然导致事件B发生，表示为A⊆B。 - **相等关系**：如果两个事件A和B的发生完全相同，我们写成A=B。 - **积事件**：事件A和B同时发生，记为AB。 - **和事件**：事件A或B至少有一个发生，记为A∪B。 - **差事件**：事件A发生而B不发生，记为A-B。 - **互斥事件**：事件A和B不可能同时发生，即A∩B=∅，也称它们为互不相容事件。 - **逆事件**：事件A的逆事件是"A不发生"，记为A'，A和A'互为对立事件，即A∪A'=Ω（样本空间）。 2. **事件的运算律** - **交换律**：A∪B=B∪A，A∩B=B∩A。 - **结合律**：(A∪B)∪C=A∪(B∪C)，(A∩B)∩C=A∩(B∩C)。 - **分配律**：A∪(B∩C)=(A∪B)∩(A∪C)，A∩(B∪C)=(A∩B)∪(A∩C)。 - **对偶律（德摩根律）**：A∪B'=A'∩B'，A∩B'=A'∪B'。 - **减法**：A-(B∪C)=A∩B'∩C'，A-(B∩C)=A-(A∩B)∪(A∩C')。 3. **概率的定义与性质** - **频率定义**：在大量重复试验中，事件A发生的频率趋于稳定值P，P即为事件A的概率，记为P(A)。 - **公理化定义**： - 非负性：P(A)≥0。 - 规范性：P(S)=1，其中S是样本空间。 - 可列可加性：若事件Ai两两互斥，那么P(A1∪A2∪...)=P(A1)+P(A2)+...。 4. **概率性质** - **有限可加性**：对于有限个两两互斥的事件Ai，有P(A1∪A2∪...∪An)=P(A1)+P(A2)+...+P(An)。 - **对立事件**：若B是A的对立事件，则P(A)+P(B)=1。 - **概率的非负性和上限**：0≤P(A)≤1。 - **乘法原理**：对于独立事件A和B，P(AB)=P(A)P(B)。 5. **组合计数原理** - **分类计数原理**：如果有k类方法，每类有mi种，完成任务的方法总数为m1+m2+...+mk。 - **分步计数原理**：若有k个步骤，每步有ni种方法，完成任务的方法总数为n1×n2×...×nk。 - **排列**：从n个不同元素中取m个进行排列，排列数为n!/(n-m)!。 - **组合**：从n个不同元素中取m个组合，组合数为C(n,m)=n!/(m!(n-m)!). 6. **等可能概型（古典概型）** - **定义**：样本点有限且等概率出现的随机试验。 - **计算公式**：事件A的概率P(A)=k/n，其中k是事件A包含的结果数，n是所有可能结果数。 7. **条件概率** - **定义**：已知事件A发生的情况下，事件B发生的概率P(B|A)。 - **计算公式**：P(B|A)=P(AB)/P(A)。 在实际问题中，概率论与数理统计的知识被广泛应用于数据分析、决策制定、风险评估等多个领域，是理解复杂随机现象的关键工具。通过深入理解和熟练运用这些概念，我们可以更好地预测和解释不确定性事件。