PB16110173-徐煜森-project31

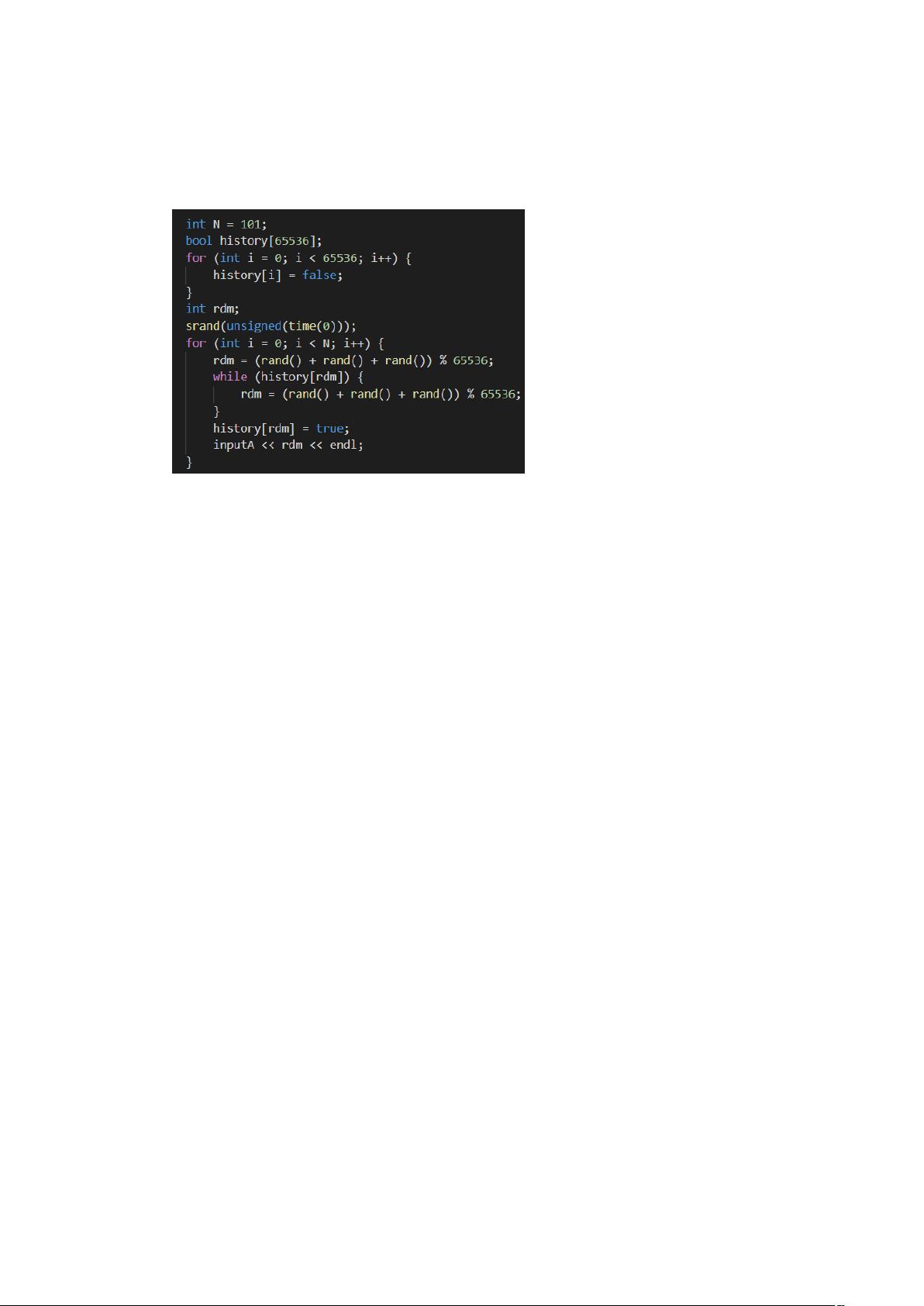
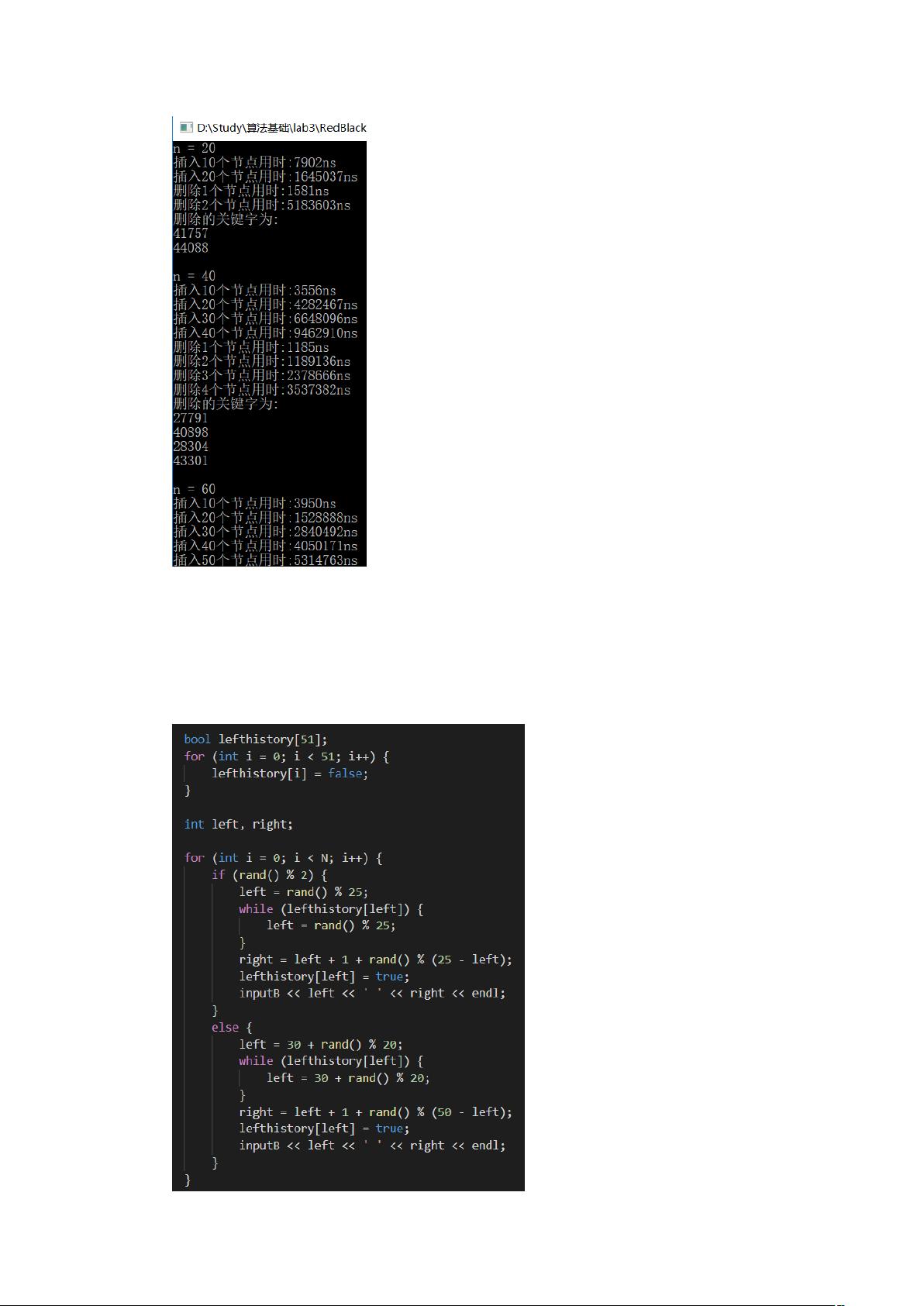
【红黑树与区间树实验】 红黑树是一种自平衡二叉查找树，它具有以下性质： 1. 每个节点要么是红色，要么是黑色。 2. 根节点是黑色。 3. 每个叶节点（NIL或空节点）是黑色。 4. 如果一个节点是红色，则它的子节点必须是黑色。 5. 对每个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点。 在实验1中，徐煜森实现了红黑树的基本算法，包括插入和删除操作。对于不同规模的输入（20, 40, 60, 80, 100个节点），他观察到插入和删除的时间性能。虽然期望的复杂度是O(logn)，但在较小规模的数据下，运行时间更接近线性，这可能是由于fixup函数的调用时间和硬件因素的影响。 在实验2中，区间树被实现，它是一种特殊类型的红黑树，用于存储具有区间属性的数据。区间树的关键特性在于可以快速查找与给定值重叠的区间。徐煜森在区间树中增加了对节点最大值的维护，使得插入、删除、遍历和查找区间变得更加高效。 关键代码部分涉及了红黑树的旋转、插入、删除及其修正操作，以及区间树中对节点max值的维护。旋转操作包括左旋和右旋，用于在插入或删除后保持树的平衡。插入和删除操作会触发相应的修正函数，以确保红黑树的性质得以维持。在区间树中，还需要额外更新max值，以反映区间的变化。 实验结果显示，无论是插入还是删除，当节点数量较少时，运行时间似乎与节点数成线性关系，而不是期望的对数关系。这可能是由于在小规模数据下，修复操作的时间成本相对较高，或者是由于系统缓存的影响。对比C++标准库中的红黑树实现（如`std::set`），得到了相似的结果。 这个实验揭示了红黑树和区间树在实际应用中的性能特点，以及在不同规模数据下性能的微妙变化。在设计和实现自定义数据结构时，需要考虑到这些因素，以便优化算法以适应特定场景的需求。同时，实验也强调了在进行性能测试时，理解并考虑底层实现细节和环境因素的重要性。