徐煜森-PB16110173-Report31

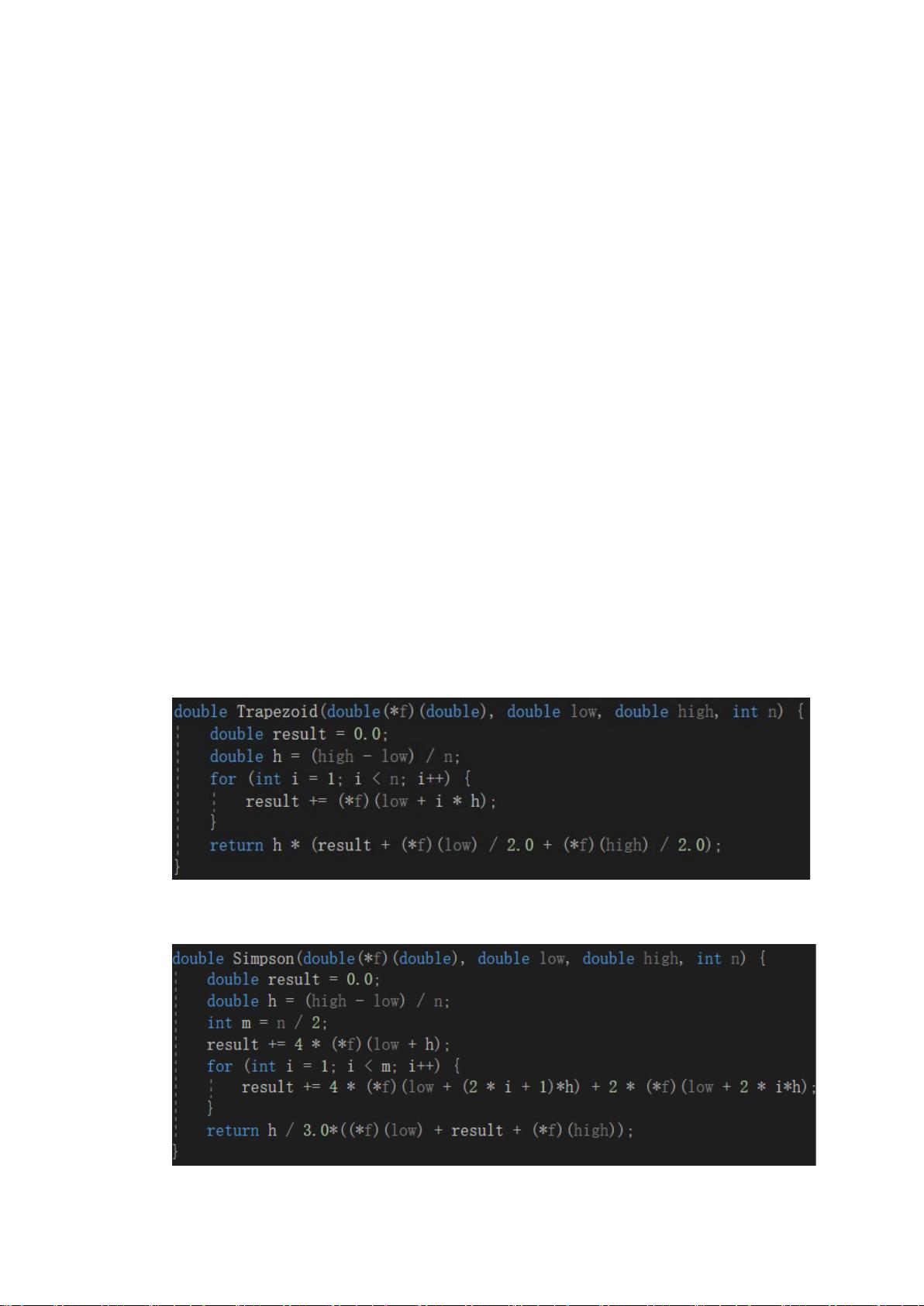
报告31是由学生徐煜森完成的一份关于数值积分算法分析的实验报告，主要探讨了复化梯形积分和复化Simpson积分方法。在实验中，他使用这两种方法计算了一个特定的积分问题，并对计算结果进行了分析和比较。 1. 算法分析： 在本次实验中，徐煜森采用复化梯形积分和复化Simpson积分来求解积分问题：∫ sin(x^6) dx，其中x的范围未明确给出，但积分区间被等距分割。为了实现算法的通用性，他利用函数指针传递需要积分的函数、积分区间以及节点数。算法的核心部分是两个循环，循环变量k分别用于调用复化梯形积分和复化Simpson积分的计算函数。 复化梯形积分是一种基于梯形法则的数值积分方法，通过将积分区间分解成多个子区间并累加每个子区间的梯形面积来近似原积分。 复化Simpson积分则是基于Simpson法则，它在每个子区间上使用二次多项式进行插值，然后求和这些二次多项式的积分。这种方法通常比梯形法则更精确，因为它考虑了函数的曲率。 2. 计算结果： 实验结果显示了随着节点数K增加，两种积分方法的误差均逐渐减小，误差阶趋于稳定。复化梯形积分的误差阶接近理论值2，而复化Simpson积分在K较小的时候误差阶接近4（理论上误差阶为4）。 然而，当K达到12时，复化Simpson积分的误差阶出现波动。这可能是因为在计算过程中，对于某些特定的K值，函数在积分区间内的变化非常小，导致近似误差在计算过程中被放大。 3. 结果分析与对比： 通过对结果的分析，可以得出以下几点： - 当K值相同时，复化Simpson积分的误差小于复化梯形积分，这表明复化Simpson积分具有更高的精度。 - 误差阶的稳定性反映了算法的收敛性。复化梯形积分的误差阶稳定在2，符合其理论预期；而复化Simpson积分在大部分情况下误差阶接近4，但在K=12时有异常，这可能是由于近似误差在计算过程中的敏感性。 - 根据误差阶的理论值（代数精度+1），可以推断复化Simpson积分的代数精度为3，高于复化梯形积分的2，进一步证明了复化Simpson积分的优越性。 总结： 实验表明，复化Simpson积分在处理给定积分问题时，不仅具有更小的计算误差，而且其代数精度更高，因此在实际应用中更优。然而，当积分区间和函数特性使得积分结果非常接近时，可能会出现较大的误差波动，这是需要注意的问题。在数值积分中选择合适的方法取决于具体问题的需求和函数的性质。