数据结构之堆1

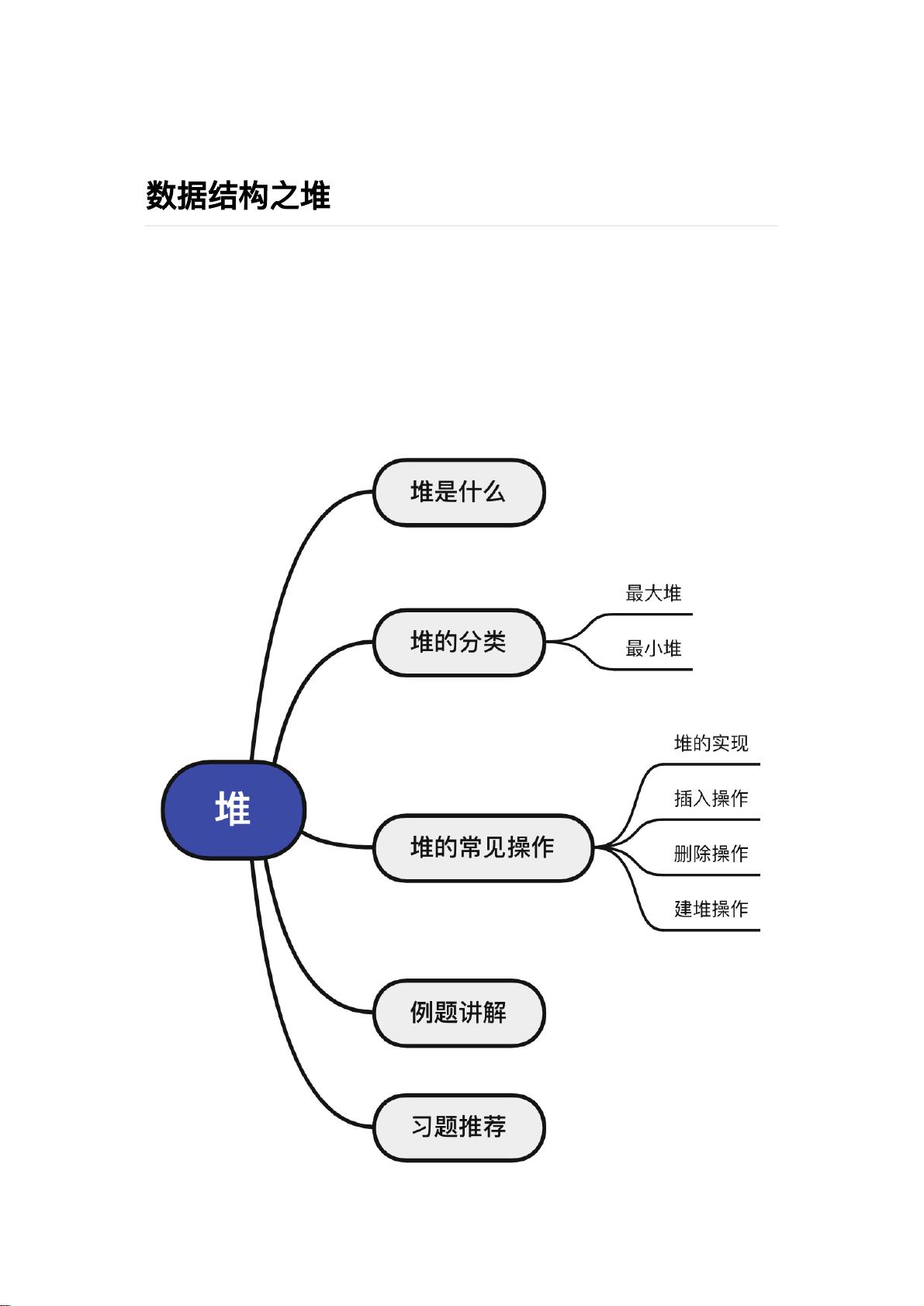
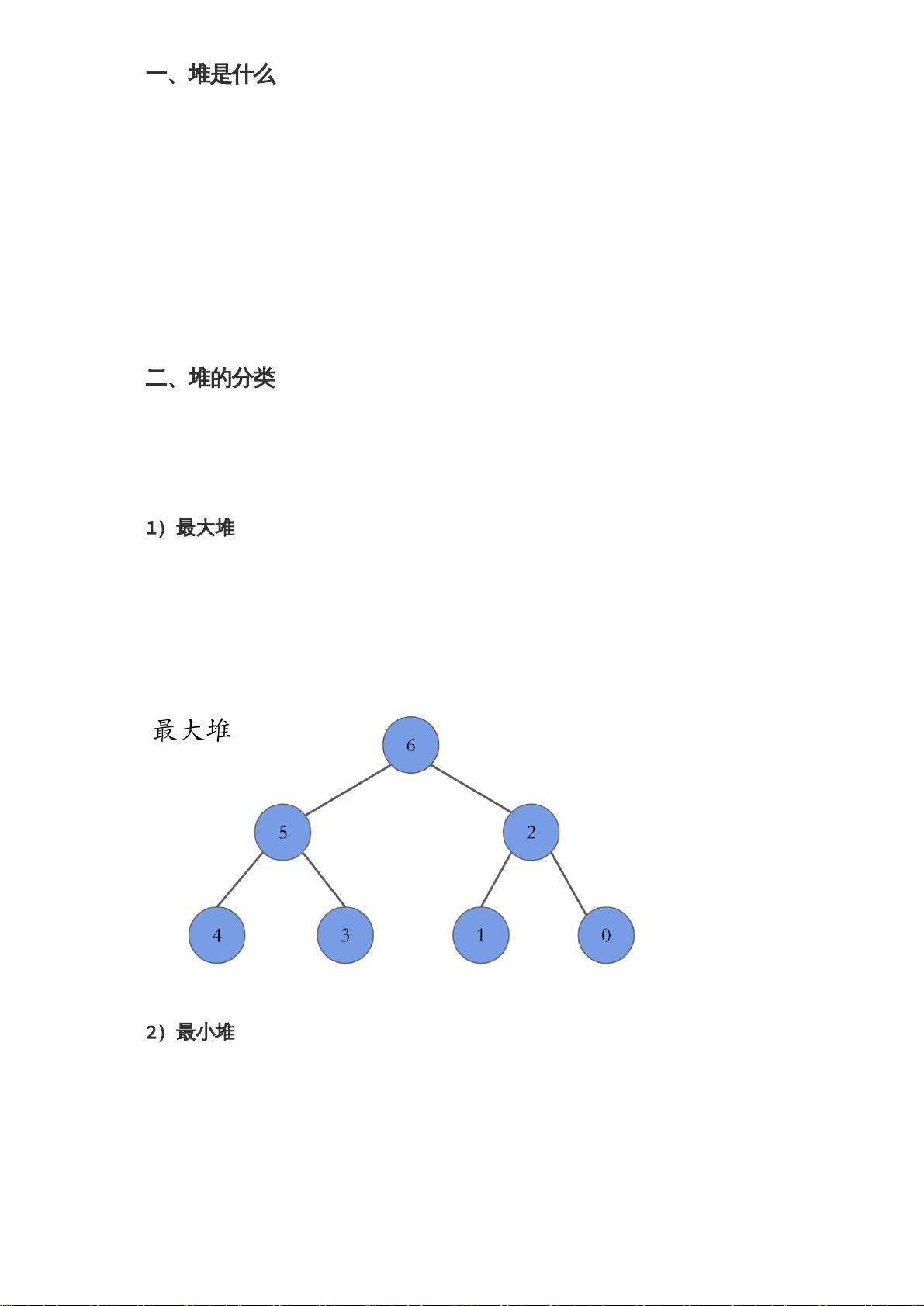
【数据结构之堆1】是关于数据结构中堆的详细解析，主要涵盖了堆的概念、分类、常见操作以及在LeetCode等刷题平台上的应用。堆作为一种特殊的完全二叉树，通常用于实现优先队列，以高效地进行最大值或最小值的查找、插入和删除。 **1. 堆的定义** 堆是一种特殊的完全二叉树，分为最大堆和最小堆。最大堆中，每个父节点的值大于或等于其子节点的值，堆顶元素为整个堆的最大元素。相反，最小堆中，每个父节点的值小于或等于子节点的值，堆顶元素为最小值。 **2. 堆的分类** - **最大堆**：每个节点的值大于或等于其子节点的值，堆顶元素为最大值。 - **最小堆**：每个节点的值小于或等于其子节点的值，堆顶元素为最小值。 **3. 堆的实现** 通常使用数组来存储堆，因为堆满足完全二叉树的特性，可以使用数组下标轻松表示父子节点关系。例如，对于下标为i的节点，其父节点下标为 (i-1)/2，左子节点下标为2i+1，右子节点下标为2i+2。 **4. 常见操作** - **插入操作**：新元素插入到数组末尾，然后通过“向上调整法”保证堆的性质，即如果新节点的值大于其父节点，就与其交换位置，直到满足堆的性质或达到根节点，时间复杂度为O(logn)。 - **删除操作**：最常用的删除方法是“向下调整法”，将根节点与最后一个叶子节点交换，删除叶子节点，然后调整新根节点到正确位置，时间复杂度也为O(logn)。 - **建堆操作**：可以使用排序、逐个插入或自底向上调整等方法，其中自底向上调整的时间复杂度为O(n)。 **5. 应用实例** 在LeetCode的703. 数据流中的第 K 大元素问题中，可以利用最小堆来解决。保持堆内元素数量不超过K，每次添加新元素后，如果堆大小超过K，就移除堆顶元素（最小值）。这样，堆顶元素始终为当前数据流中的第K大元素。 通过以上介绍，我们可以理解堆在解决实际问题中的重要性，特别是在需要高效处理最大值和最小值场景下的优势。学习和掌握堆的数据结构，对于提升算法能力和解决编程问题具有重要意义。