
2018/8/21
1
本节内容
树的基本概
念
王道考研/CSKAOYAN.COM
王道考研/CSKAOYAN.COM
树
a1
a2
一对一的线性结构
a3
a4 a5
一对多的树性结构
树是递归定义的结构
树是N(N≥0)个结点的有限集合,N=0
时,称为空树,这是一种特殊情况。在
任意一棵非空树中应满足:
1)有且仅有一个特定的称为根的结点。
2)当N>1时,其余结点可分为m(m>0)
个互不相交的有限集合T
1
,T
2
,…,T
m
,
其中每一个集合本身又是一棵树,并且
称为根结点的子树。
a6
a5
a6
王道考研/CSKAOYAN.COM
树的相关概念
a1
a2
a3
a4 a5
a6
王道考研/CSKAOYAN.COM
树的相关概念
a1
a2
a3
a4 a5
a6
第一层
第二层
第三层

2018/8/21
2
王道考研/CSKAOYAN.COM
树的性质
1.树中的结点数等于所有结点的度数加1。
a1
a2
a3
a4 a5
a6
证明:不难想象,除根结点以外,每
个结点有且仅有一个指向它的前驱结
点。也就是说每个结点和指向它的分
支一一对应。
假设树中一共有b个分支,那么除了根
结点,整个树就包含有b个结点,所以
整个树的结点数就是这b个结点加上根
结点,设为n,则n=b+1。而分支数b
也就是所有结点的度数,证毕。
王道考研/CSKAOYAN.COM
树的性质
2.度为m的树中第i层上至多有m
i
−1个结点(i≥1)。
root
证明:(数学归纳法)
首先考虑i=1的情况:第一层只有根结点,即一个结点,i=1带入
式子满足。
假设第i-1层满足这个性质,第i-1层最多有m
i-2
个结点。
………
........
..
i-1层
………
又因为树的度为m,所以对于第i-1层的每个结点,最多
有m个孩子结点。所以第i层的结点数最多是i-1层的m
倍,所以第i层上最多有m
i-1
个结点。
最多m个
最多m
i-2
个
王道考研/CSKAOYAN.COM
树的性质
3.高度为h的m叉树至多有(m
h
-1)/(m-1)个结点
证明:(利用性质2:度为m的树中第i层上至多有m
i−1
个结点)
所以高度为h的m叉树至多有
N=m
0
+m
1
+m
2
+m
3
+…m
h-2
+m
h-1
=m
0
(1-m
h
)/(1-m) (等比数列求和公式)
=(m
h
-1)/(m-1)
4.具有n个结点的m叉树的最小高度为 log
m
(n(m-1)+1)
最小高度时,这个树是一个满m叉树。
由性质3,知道满m叉树的结点数为(m
h
-1)/(m-1)。
于是(m
h
-1)/(m-1)=n 解这个方程,可以得到
h=log
m
(n(m-1)+1)。
因为这个是高度,是整数,所以要向上取整。
a1
a4
a2
a3
a6
a5 a7
满二叉树
本节内容
树的存储结
构
王道考研/CSKAOYAN.COM

2018/8/21
3
王道考研/CSKAOYAN.COM
顺序存储结构
双亲表示法:用一组连续的存储空间存储树的结点,同时在每个结点中,用一个变量存储该结点的双亲结点在
数组中的位置。
typedef char ElemType;
typedef struct TNode{
ElemType data; //结点数据
int parent; //该结点双亲在数组中的下标
}TNode; //结点数据类型
data
parent
结点类型
#define Maxsize 100
typedef struct {
TNode nodes[MaxSize]; //结点数组
int n; //结点数量
}Tree; //树的双亲表示结构
data
parent
data
parent
………
………
树
王道考研/CSKAOYAN.COM
顺序存储结构
a
d
b
c
e f
data parent
a
b
c
d
e
f
-1
0
下标
0
1
2
3
4
5
0
1
1
2
双亲表示法可以根据parent值找到该结点的双亲结点,时间复杂度为O(1)。
可是如果想找某个结点的孩子结点?
王道考研/CSKAOYAN.COM
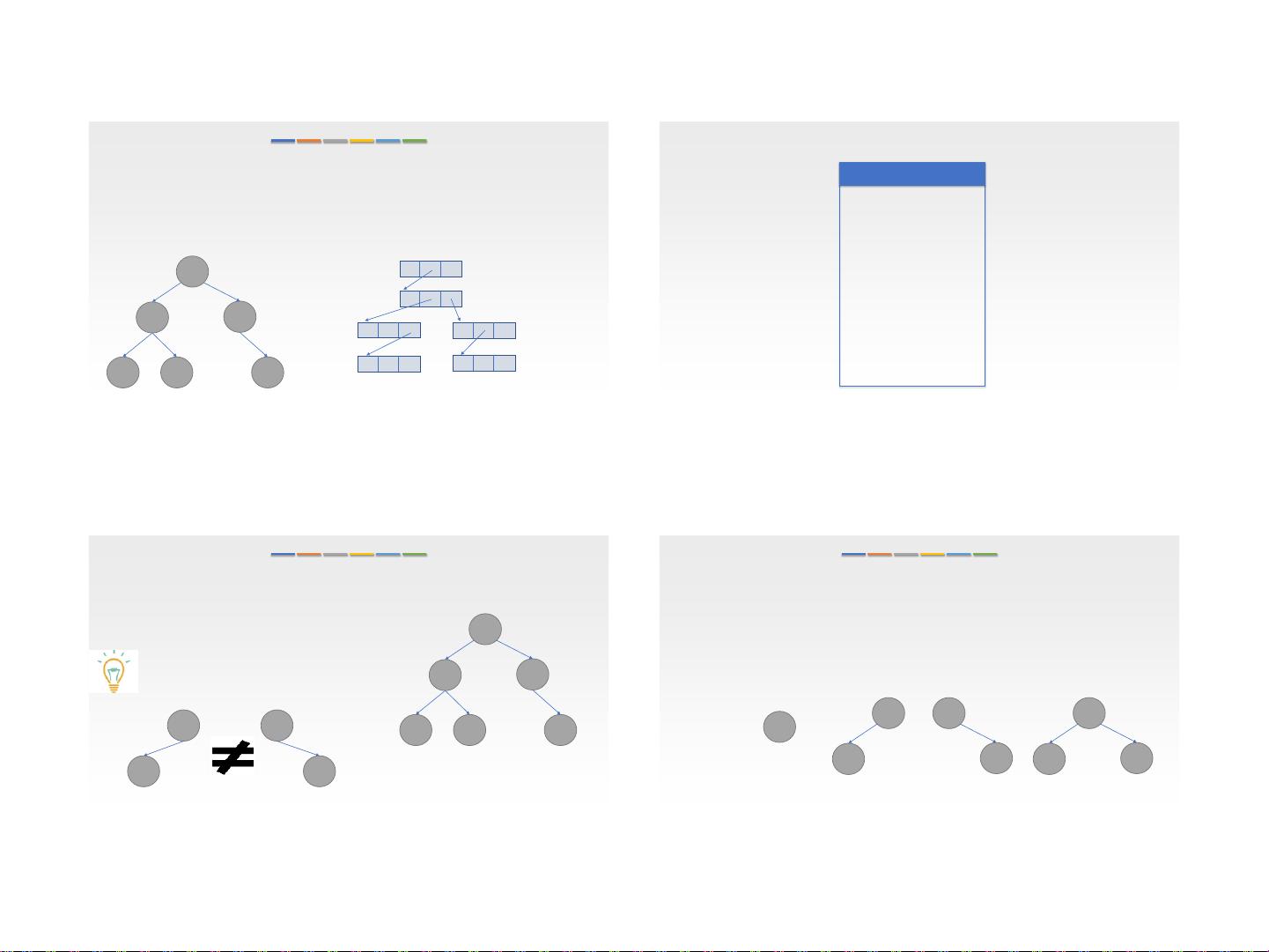
链式存储结构(1)
孩子表示法:把每个结点的孩子结点排列起来存储成一个单链表。所以n个结点就有n个链表;
如果是叶子结点,那这个结点的孩子单链表就是空的;
然后n个单链表的的头指针又存储在一个顺序表(数组)中。
需要设计两种结点结构类型:一是孩子链表的孩子结点,二是每个孩子链表的表头结点(存在
数组中)。
typedef char ElemType;
typedef struct CNode{
int child; //该孩子在表头数组的下标
struct CNode *next; //指向该结点的下一个孩子结点
}CNode,*Child; //孩子结点数据类型
typedef struct {
Elemtype data; //结点数据域
Child firstchild; //指向该结点的第一个孩子结点
}TNode; //孩子结点数据类型
王道考研/CSKAOYAN.COM
链式存储结构(1)
a
d
b
c
e f
data
parent
a
b
c
d
e
f
-1
0
下标
0
1
2
3
4
5
0
1
1
2
firstchild
^
^
^
1
3
5
2
4
^
^
^
#define Maxsize 100
typedef struct {
TNode nodes[Maxsize]; //结点数据域
int n; //树中结点个数
}Tree; //树的孩子表示结构
2018/8/21
4
王道考研/CSKAOYAN.COM
链式存储结构(2)
孩子兄弟表示法:顾名思义就是要存储孩子和孩子结点的兄弟,具体来说,就是设置两个指针,分别指向该结
点的第一个孩子结点和这个孩子结点的右兄弟结点。
typedef char ElemType;
typedef struct CSNode{
ElemType data; //该结点的数据域
struct CSNode *firstchild,*rightsib; //指向该结点的第一个孩子结点和该结点的右兄弟结点
}CSNode; //孩子兄弟结点数据类型
a
d
b
c
e f
a
b
d
e
c
f
^
^ ^
^
^
^
^
^
本节内容
二叉树
王道考研/CSKAOYAN.COM
王道考研/CSKAOYAN.COM
二叉树
二叉树是n(n≥0)个结点的有限集合:
① 或者为空二叉树,即n=0。
② 或者由一个根结点和两个互不相交的被称为根的左子树
和右子树组成。左子树和右子树又分别是一棵二叉树。
A
D
B
C
E F
1.每个结点最多有两棵子树。
2.左右子树有顺序
A
B
A
B
王道考研/CSKAOYAN.COM
二叉树
二叉树的五种基本形态:
1.空树
2.只有一个根结点
3.根结点只有左子树
4.根结点只有右子树
5.根结点既有左子树又有右子树
∅
root
left
right
root
root
left
root
right

















评论30