05.EM算法1
需积分: 0 130 浏览量
更新于2022-08-03
收藏 1004KB PDF 举报
EM算法,全称为Expectation Maximization(期望最大化)算法,是一种在处理含有隐变量的数据集时,用于估计概率模型参数的迭代方法。该算法源于极大似然估计,但解决了最大似然估计在处理不完全数据时的困难。在EM算法中,数据被分为观测数据和隐藏数据两部分,通过E步骤(期望)和M步骤(最大化)交替进行,逐步逼近最优参数。
回顾极大似然估计的基本步骤:
1. 书写似然函数𝐿(𝜃) = 𝑃(𝑋|𝜃),其中𝜃是待估计的参数。
2. 将似然函数取对数,简化为 Hv(𝜃) = log𝐿(𝜃) = log(𝑃(𝑋; 𝜃))。
3. 对对数似然函数求导,并令其等于0,得到似然方程。
4. 解这个方程,获得参数估计。
在EM算法中,由于存在隐变量𝑍,我们无法直接写出似然函数𝐿(𝜃)。因此,我们需引入隐变量条件下的似然函数𝑃(𝑍|𝑋, 𝜃)和联合分布𝑃(𝑋, 𝑍|𝜃)。目标是最大化对所有可能的隐变量状态求和后的似然函数,即希尔伯特函数𝐻(𝜃) = ln𝑃(𝑋|𝜃)。
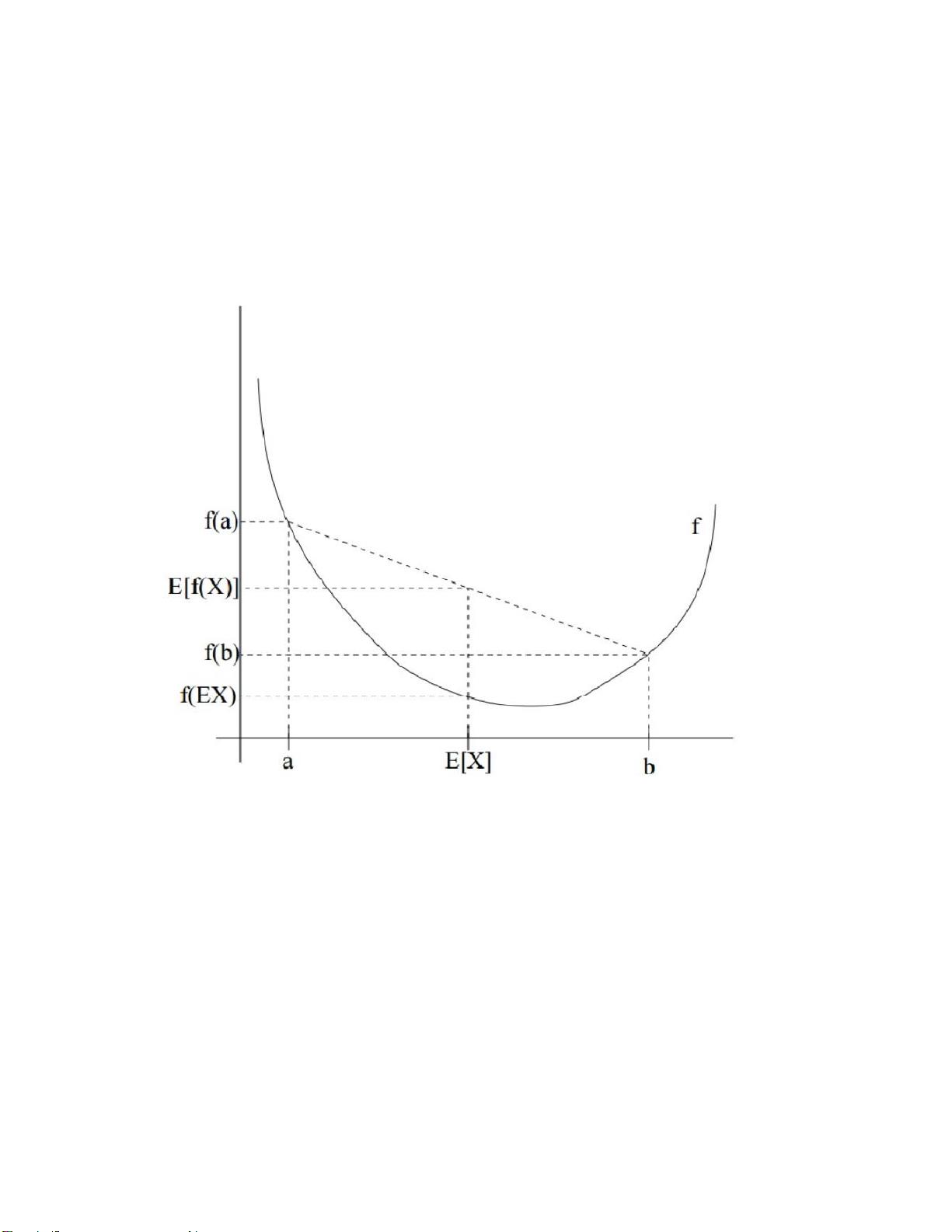
Jensen不等式在此处起关键作用。对于一个凸函数𝑓(𝑥),期望Ef[𝑓(𝑥)]总是大于等于f[E[𝑥]]。这为EM算法的推导提供了理论基础。
EM算法的具体步骤如下:
1. E步骤(期望):给定当前参数估计𝜃',计算每个观测数据点对隐变量状态的后验概率𝑞(𝑍|𝑋, 𝜃') = 𝑝(𝑍|𝑋, 𝜃')。这一步相当于估计隐变量的期望值。
2. M步骤(最大化):保持E步骤得到的分布不变,最大化Q函数𝑄(𝜃, 𝜃') = ∑𝑞(𝑍)ln 𝑝(𝑋, 𝑍|𝜃),更新参数𝜃为新的估计值,使Q函数达到最大。
这两个步骤交替进行,直到参数的改进趋近于零或者达到预设的迭代次数,从而完成参数估计。
在数学推导中,引入了Kullback-Leibler散度𝐾𝐿(𝑞||𝑝)来衡量分布𝑞(𝑍)和𝑝(𝑍|𝑋, 𝜃)的差异。当𝑞(𝑍) = 𝑝(𝑍|𝑋, 𝜃')时,KL散度最小,此时Q函数成为希尔伯特函数 Hv(𝜃) 的下界。
EM算法广泛应用于机器学习和统计建模中,例如混合高斯模型、隐马尔科夫模型等。它的优势在于能处理缺失数据和复杂的模型结构,通过迭代优化逐步逼近最优参数估计。然而,EM算法并不保证全局最优解,而是寻找局部最优,因此在实际应用中需要注意初始化和收敛条件的设置。
宝贝的麻麻
- 粉丝: 42
- 资源: 294
最新资源
- 仙岭小学结构建模revit
- 第6章习题参考答案.zip
- BeautifyAPP的产品设计(论文+源码)_kaic.zip
- 俄罗斯方块游戏系统的设计与实现(源码+论文)_kaic.zip
- 仓库管理系统的设计与实现(论文+源码)_kaic.zip
- 基于BC模式的电商平台的设计与实现(论文+源码)_kaic.zip
- 基于C#的超市收银管理系统设计与实现(论文+源码)_kaic.zip
- 妇幼保健信息管理系统设计(论文+源码)_kaic.zip
- 基于Java技术的养生知识管理系统设计与实现(论文+源码)_kaic.zip
- 基于springboot框架的高校就业管理系统设计与实现(论文+源码)_kaic.zip
- 基于web的电影购票管理系统的设计与实现(论文+源码)_kaic.zip
- ssm149学生成绩管理系统+vue.rar
- 深度报告:CPU研究框架.pdf
- Freertos-freertos
- BootstrapAdmin-c#
- XTools-idea