《大学计算机-计算思维导论》19-20学时-递归-ding-20201

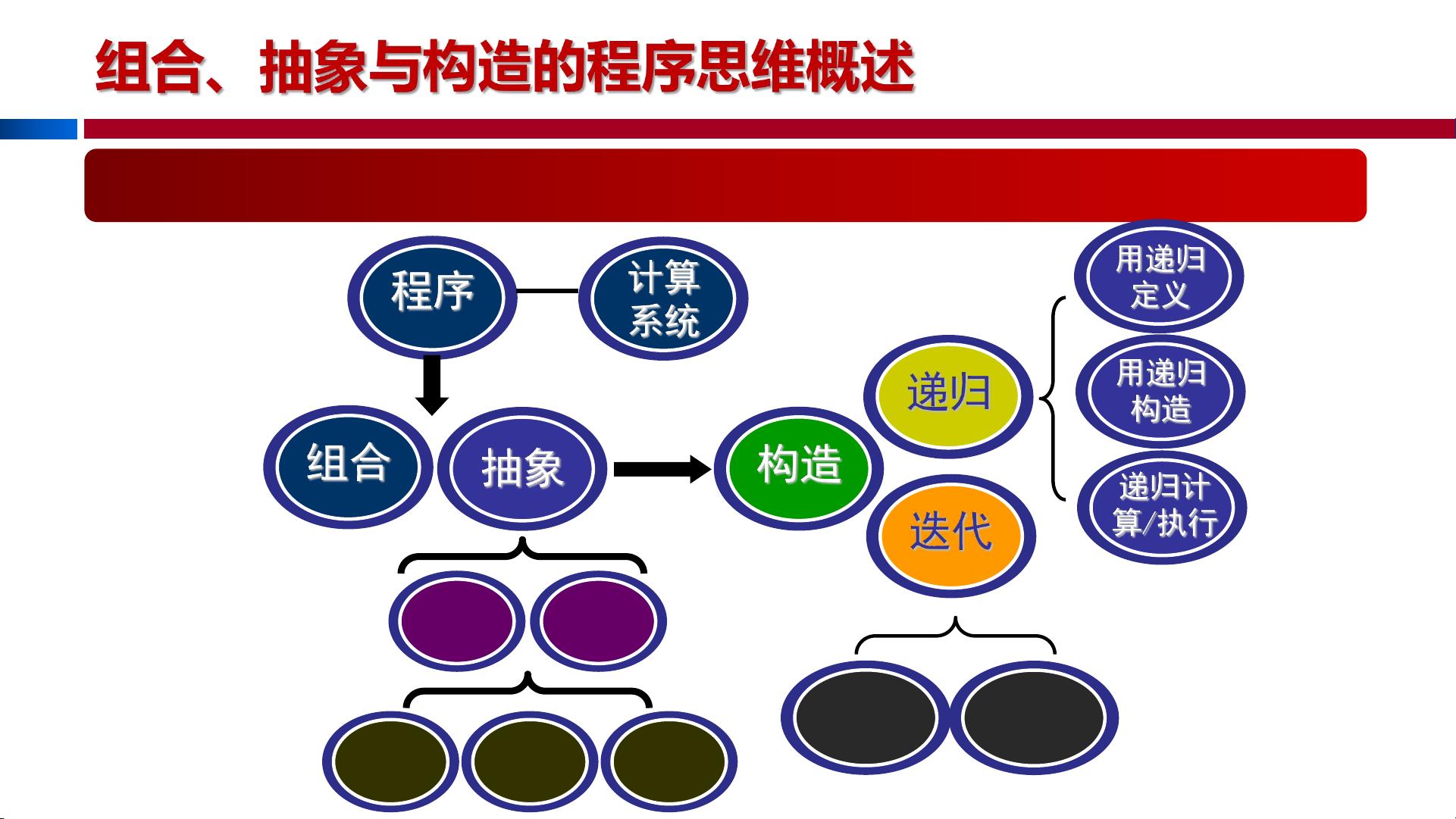
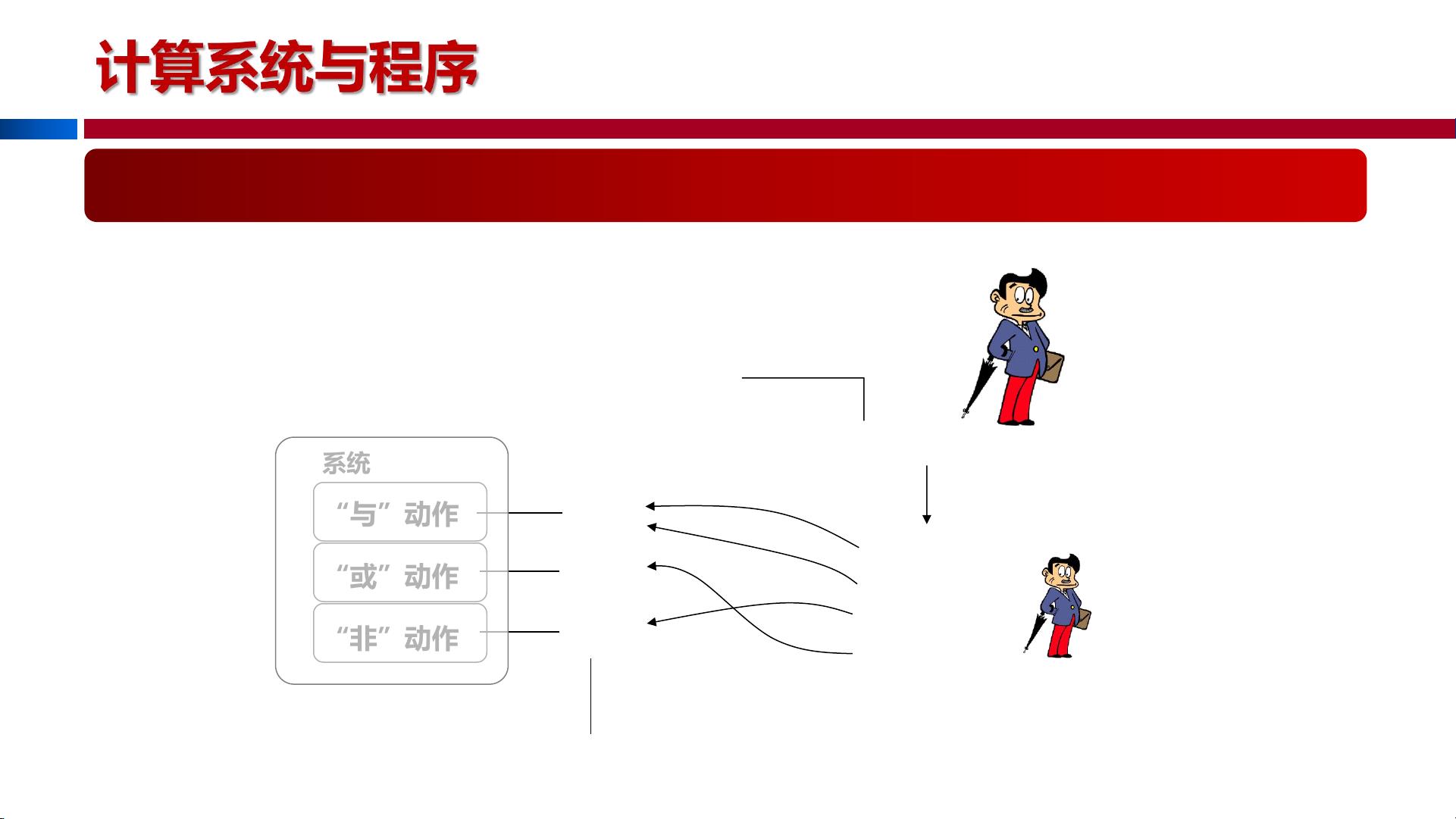
《大学计算机-计算思维导论》课程中，第19-20学时重点讨论了递归和程序构造的基本概念。递归是程序构造的重要手段之一，它涉及到计算系统与程序的关系，以及如何通过基本动作的组合来实现复杂的计算。 递归是一种自包含的解决问题的方法，其中一个问题的解决方案依赖于较小规模相同问题的解决方案。原始递归函数是递归的基础，它们可以通过组合和递归的方式定义。复合是指将简单函数合并为更复杂的函数，而递归则是通过调用自身来解决问题。递归函数分为两种类型：直接递归和间接递归。递归与迭代是两种常见的程序执行策略，它们都可以用来解决相同的问题，但执行机制不同。在理解递归和迭代的过程中，关键在于掌握如何设计递归函数，并理解其执行过程。 计算系统的核心是计算对象，它包括基本的运算符（即函数），这些运算符可以定义并执行对数据的操作。在最基本的层面上，这些运算符包括逻辑运算如“与”、“或”和“非”。通过组合这些基本运算符，可以构建更复杂的逻辑表达式，甚至模拟加减乘除等算术运算。例如，加减法可以转换为逻辑运算，进而实现加减乘除的逻辑化表示。 程序的构造通常包括三个主要步骤：定义、构造和执行。在定义阶段，我们需要明确计算的对象和操作。构造阶段涉及将基本动作（如逻辑运算）组合成指令，形成执行序列。执行阶段则由程序执行机构负责，它解释指令并按照顺序调用基本动作来完成计算任务。计算系统不仅仅是基本动作的集合，还包括控制这些动作执行的指令，以及负责解释和执行指令的程序执行机构。 程序的作用和本质在于通过抽象和组合实现复杂动作。在更高的抽象层次上，我们可以定义新的指令，这些指令是由低层次系统实现的更复杂操作的封装。这种分层构造使得程序设计更加模块化，更易于理解和维护。例如，基本的算术运算如加、减、乘、除，可以作为更高层次的指令使用，它们是通过基本的逻辑运算组合实现的。 在编程中，我们经常使用中缀表示法（运算符在数值之间）或前缀表示法（运算符在数值之前）来表达运算组合式。运算组合式是程序的一种表达形式，它允许我们用简洁的方式描述一系列计算。例如，`(+ 100 205)` 表示100和205的和，而`(- 200 50)`则表示200减去50的结果。 递归是程序设计中的强大工具，它可以帮助我们以简洁和优雅的方式解决复杂问题。通过理解和掌握递归原理，我们可以更深入地理解计算系统的运作机制，从而更好地设计和实现计算程序。