PCA_主成分分析1

PCA（主成分分析）是一种广泛应用于数据分析领域的统计技术，主要用于高维数据的降维处理。它的核心思想是通过线性变换找到数据集的新坐标系，使得数据在新坐标系下的投影能够最大程度地保留原始数据的信息，同时使得这些新坐标轴（主成分）之间互为正交，且按照数据方差的大小排序。这样，我们就可以通过选取方差较大的前几个主成分来降低数据的维度，同时保持大部分的信息。 PCA 的具体步骤如下： 1. 数据预处理：将原始数据按列组成一个 n 行 m 列的矩阵 X，其中 n 为样本数量，m 为特征数量。接着，对矩阵 X 的每一行（每个特征字段）进行零均值化，即将每一行的均值减去，确保数据的中心化，这一步是为了消除数据量纲的影响，使得后续计算更为合理。 2. 计算协方差矩阵：对零均值化的数据矩阵 X 计算其协方差矩阵，协方差矩阵反映了各个特征之间的相关性。协方差矩阵的元素是对角线上的每个特征的方差和非对角线上的特征之间的协方差。 3. 求解特征值与特征向量：对协方差矩阵求解特征值 λ 和对应的特征向量。特征值代表了各个主成分的重要性，即数据在相应方向上的方差；特征向量则指示了数据在新坐标系中的方向。 4. 排序与选择：将特征向量按照对应的特征值大小进行排序，大的特征值对应的特征向量表示了数据的主要变化方向。通常，我们会选取最大的 k 个特征值对应的特征向量，组成一个 k × m 的矩阵 P。 5. 数据降维：将原始数据矩阵 X 乘以特征向量矩阵 P 的转置，得到降维后的新数据矩阵，这个新矩阵的行数不变，列数减少为 k，即实现了数据的降维。 PCA 在多个场景中有广泛应用，如： 1. 非监督学习：PCA 是一种无监督的学习方法，适用于那些没有标签或者分类信息的数据集。 2. 特征选择：PCA 允许用户根据方差比例自主决定保留多少特征，从而控制降维后的数据信息损失。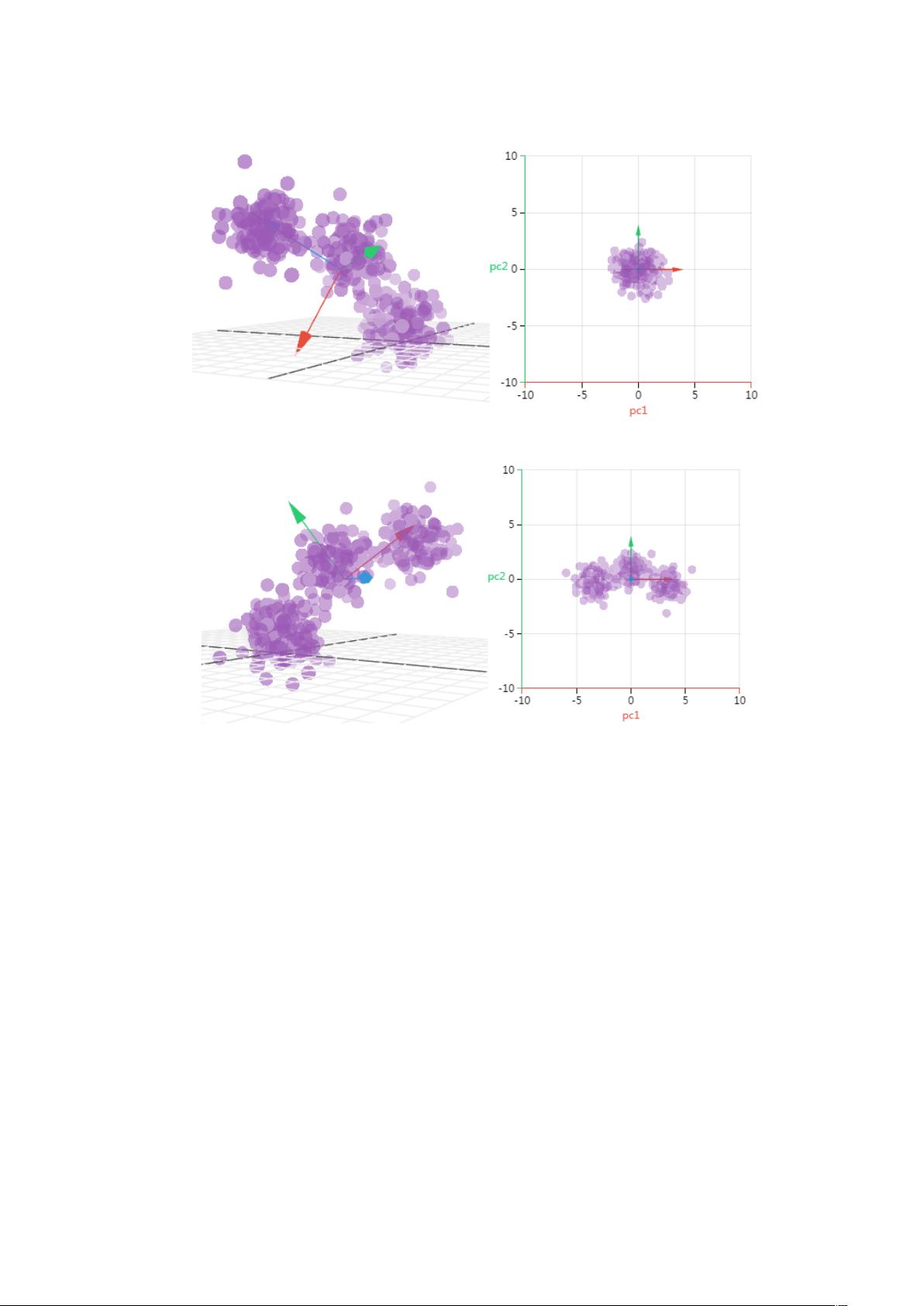 3. 数据可视化：在高维数据中，PCA 可以帮助我们将数据投影到二维或三维空间，便于观察和理解数据结构。 4. 提升算法效率：降维后，计算复杂度降低，尤其对于大数据集，PCA 能显著提高算法的运行速度和降低内存需求。 5. 去噪：PCA 可以通过去除低方差的特征来减少噪声影响。 除了 PCA，还有其他降维方法，如奇异值分解（SVD）、因子分析（FA）、独立成分分析（ICA）等。这些方法各有优缺点，选择哪种方法取决于具体的应用需求和数据特性。降维技术在机器学习、图像处理、生物信息学等多个领域都扮演着重要的角色，它简化了数据处理，提高了模型的效率和解释性，同时也为复杂数据的可视化提供了可能。