考研数学历年真题(1998-2007)年数学二1

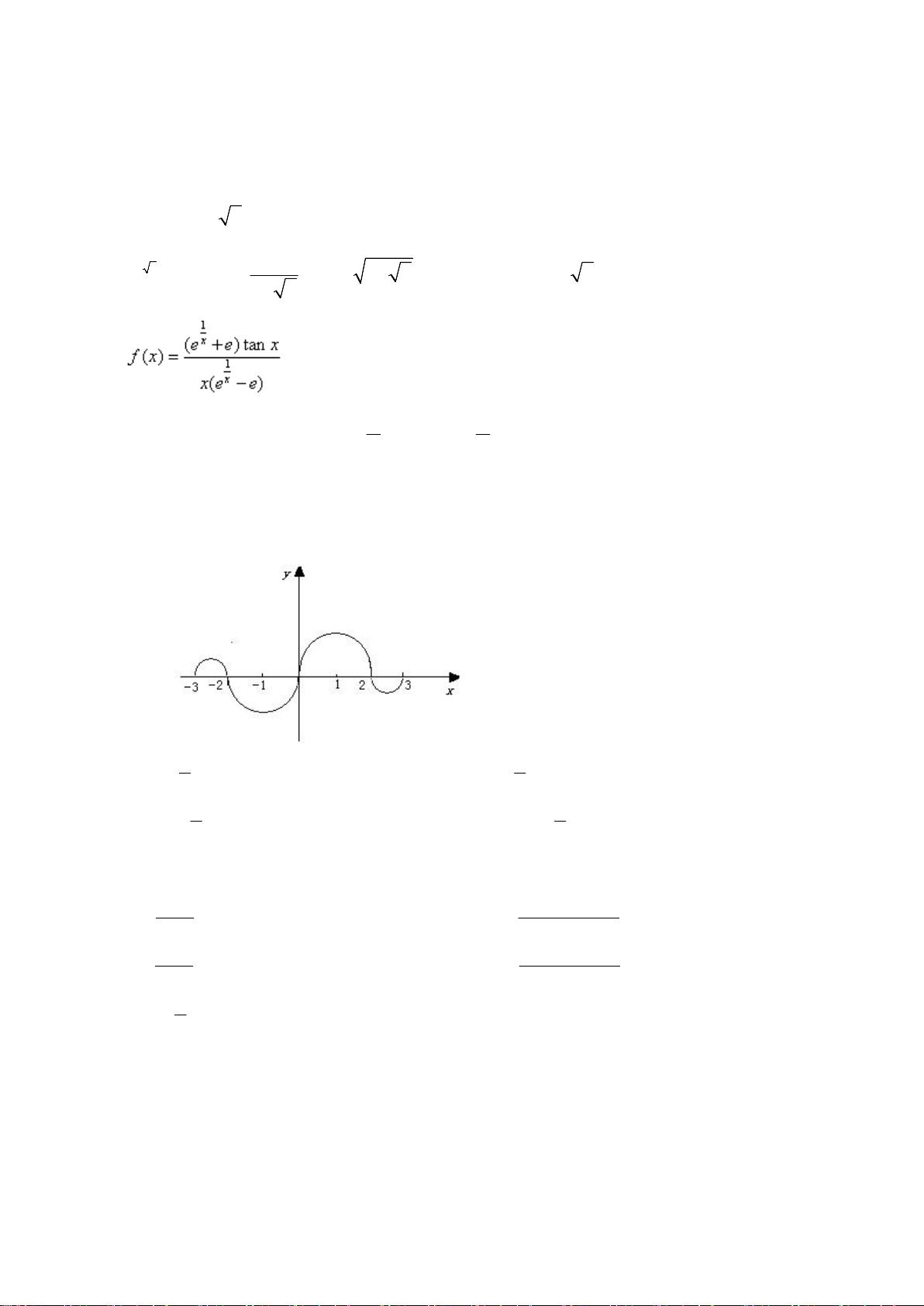
【考研数学历年真题(1998-2007)年数学二1】是一份关于考研数学二科目的历年真题集，主要涵盖了选择题和填空题两种题型，旨在测试考生对高等数学相关知识的掌握程度。这份试题涉及到的知识点包括无穷小的比较、函数的间断点类型、定积分的应用、极限的存在性及其性质、曲线的渐近线、数列的收敛性、多元函数的可微性、二次积分的计算、线性代数中的向量组线性相关性以及矩阵的性质等。 1. **无穷小的比较**：题目（1）考查了无穷小量的等价关系，要求判断随着x趋近于0，哪些量与x等价。这涉及到了高阶无穷小的概念，答案是与x等价的无穷小量是\(1 - e^x\)。 2. **函数的间断点**：题目（2）询问函数在某点的间断点类型，这需要识别第一类间断点（跳跃间断点、可去间断点、无穷间断点）。 3. **定积分的应用**：题目（3）通过一个几何问题考察定积分的几何意义，即计算面积，要求判断哪个结论正确，这需要理解定积分与面积的关系。 4. **极限的存在性及其性质**：题目（4）至（6）涉及到极限的性质，如左极限、右极限的存在性与函数值的关系，以及函数的二阶导数与数列收敛性的关系。 5. **曲线的渐近线**：题目（5）要求确定曲线的渐近线数量，这涉及到渐近线的分类：水平渐近线、垂直渐近线和斜渐近线。 6. **数列的收敛性**：题目（6）讨论了两个数列的乘积的收敛性，根据数列的比较准则来判断。 7. **多元函数的可微性**：题目（7）是关于二元函数在某点可微的充分条件，涉及到偏导数、方向导数以及Jacobian矩阵。 8. **二次积分的计算**：题目（8）涉及到了积分的几何意义，计算曲面下的面积，需要利用极坐标进行变换。 9. **线性代数中的向量组线性相关性**：题目（9）通过向量组的线性组合，考察线性相关性和线性无关性的概念。 10. **矩阵的性质**：题目（10）讨论了矩阵的合同关系和相似关系，这是线性代数的重要概念。 填空题部分同样涉及到了极限、曲线的切线斜率、函数的幂级数展开、二阶非齐次微分方程的通解、偏导数的计算以及矩阵的秩等知识点。 解答题部分则要求考生解答具体问题，例如利用已知条件求解函数、计算曲线下方的面积、分析函数的性质、求解微分方程、证明线性相关性等，这些题目不仅检验了考生的理论知识，还考察了解题技巧和逻辑推理能力。