信号与系统实验2_截图1

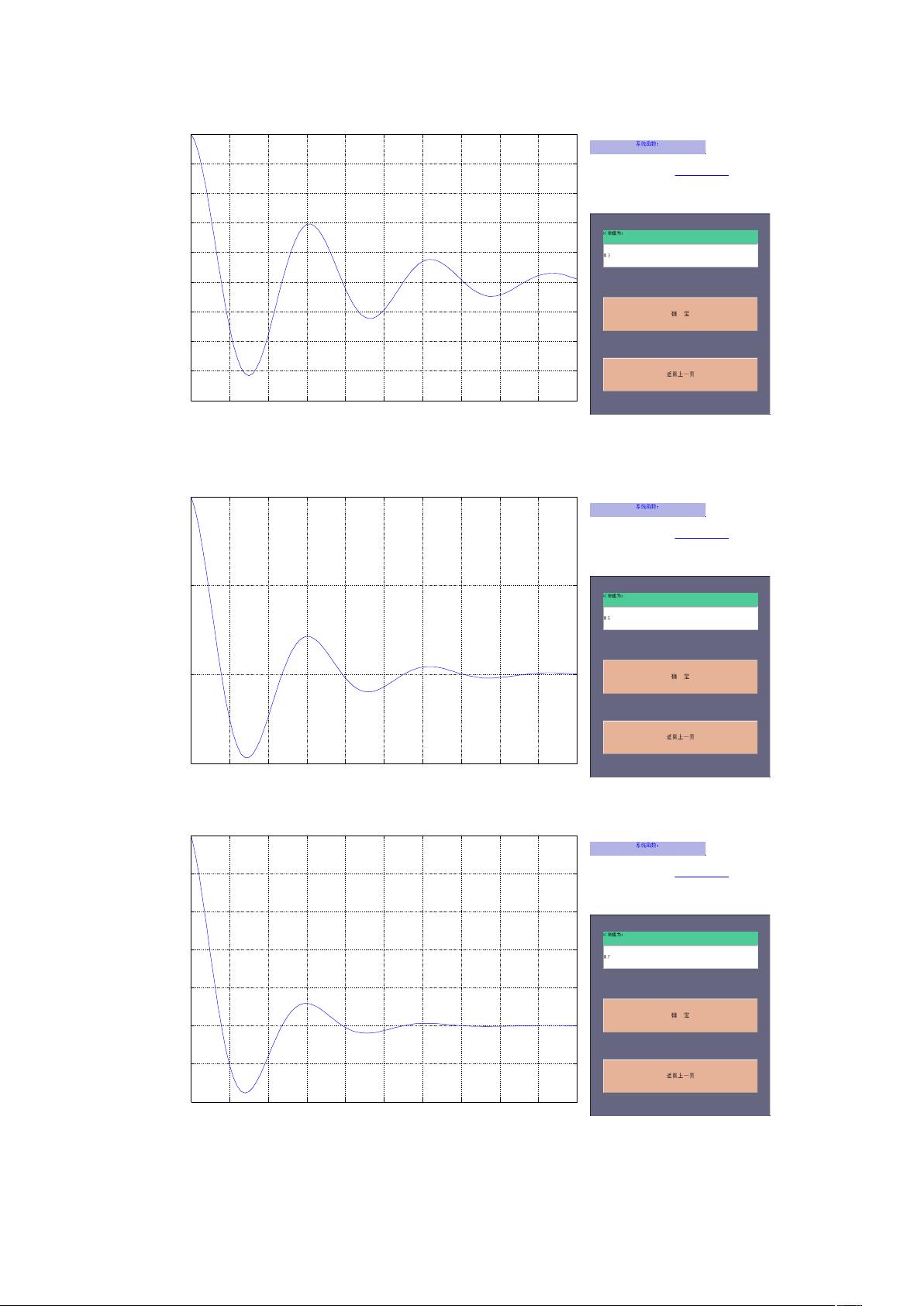
在深入探讨信号与系统的实验中，我们会聚焦于信号处理领域中至关重要的两个概念：冲激响应与单位阶跃响应，以及系统稳定性的分析。通过对实验数据的分析，我们将揭示不同系统参数配置下系统的动态行为特征和稳定性状态。 让我们探究冲激响应的概念。冲激响应是线性时不变系统（LTI系统）对一个理想冲激输入的响应。在数学中，冲激函数通常用δ(t)表示，它是一个理想化的函数，定义为在t=0时刻有无限大的值，但在其他时刻值为0，且其在全实数轴上的积分为1。在冲激响应的研究中，拉普拉斯变换是一种常用的方法，其可以将时域中的微分方程转化为s域中的代数方程。因此，系统对冲激输入的响应可以表示为某个表达式关于s的函数。例如，描述中给出了形式为(s+k)² + 4 / 10(s+k)的冲激响应函数，其中s和k是系统参数。通过进行逆拉普拉斯变换，我们可以将该函数转换为时间域内的实际响应曲线。 紧接着，我们来分析单位阶跃响应，单位阶跃响应描述的是系统对单位阶跃输入信号的反应。在数学上，单位阶跃函数通常用u(t)表示，它在t≥0时取值为1，在t<0时取值为0。在信号处理和控制系统中，单位阶跃响应是理解和分析系统动态行为的一个基本工具。通过对系统施加一个阶跃输入，我们可以观察系统随时间变化的输出响应，从而评估系统的动态特性，例如上升时间、峰值时间、超调量以及稳态值等。 在实验中，我们注意到不同系统参数（如a和b）的组合会产生不同的单位阶跃响应。例如，参数组合a=5, b=1 2 2 4，与a=4 3, b=1 2 2 4时，输出响应在峰值和达到峰值的时间上有着明显的差异。这些差异揭示了系统参数如何影响其动态行为，进而影响系统的性能表现。 系统稳定性分析是信号与系统实验的核心内容之一。稳定性分析关注的是系统对外部扰动和内部变化的抵抗能力，以及系统是否能够在受到这些干扰后恢复或保持其性能。根据拉普拉斯变换理论，系统的稳定性可以通过分析系统函数的所有极点来确定。如果所有极点都位于复平面的左半部，系统是稳定的；如果所有极点都位于虚轴上或复平面右半部，系统是不稳定的。在临界稳定状态下，系统的极点会位于虚轴上或在复平面上的实部为零。在实验数据中，通过对不同参数组合下的系统单位阶跃响应曲线的分析，我们可以判断系统的稳定性状态。例如，对于参数组合a=1 3, b=1 2 3 5，如果响应曲线显示出持续的振荡且没有趋于零的趋势，系统可能不稳定。而对于参数组合a=1 2 6, b=1 2 2 4，如果响应曲线最终趋于一个非零常数值，那么系统可能是稳定的。 综合实验数据和系统响应曲线，我们可以总结出，当系统的参数改变时，不仅影响了单位阶跃响应的动态特性，而且也直接关联到系统的稳定性。通过对冲激响应和单位阶跃响应的深入分析，结合稳定性理论，我们可以对系统进行有效的评估和设计，确保系统在实际应用中能够达到预期的性能和稳定性要求。 信号与系统实验2的研究成果在实际工程应用中具有重要的意义。无论是控制理论中的反馈控制系统设计，还是通信工程中的信号传输系统设计，又或者是信号处理中对信号的分析与重构，理解冲激响应、单位阶跃响应及其稳定性特征都是至关重要的。通过这些实验，工程师和研究人员能够更好地理解和设计复杂的信号处理系统，确保系统在实际操作中的可靠性和有效性。