第4次作业答案（批注）1

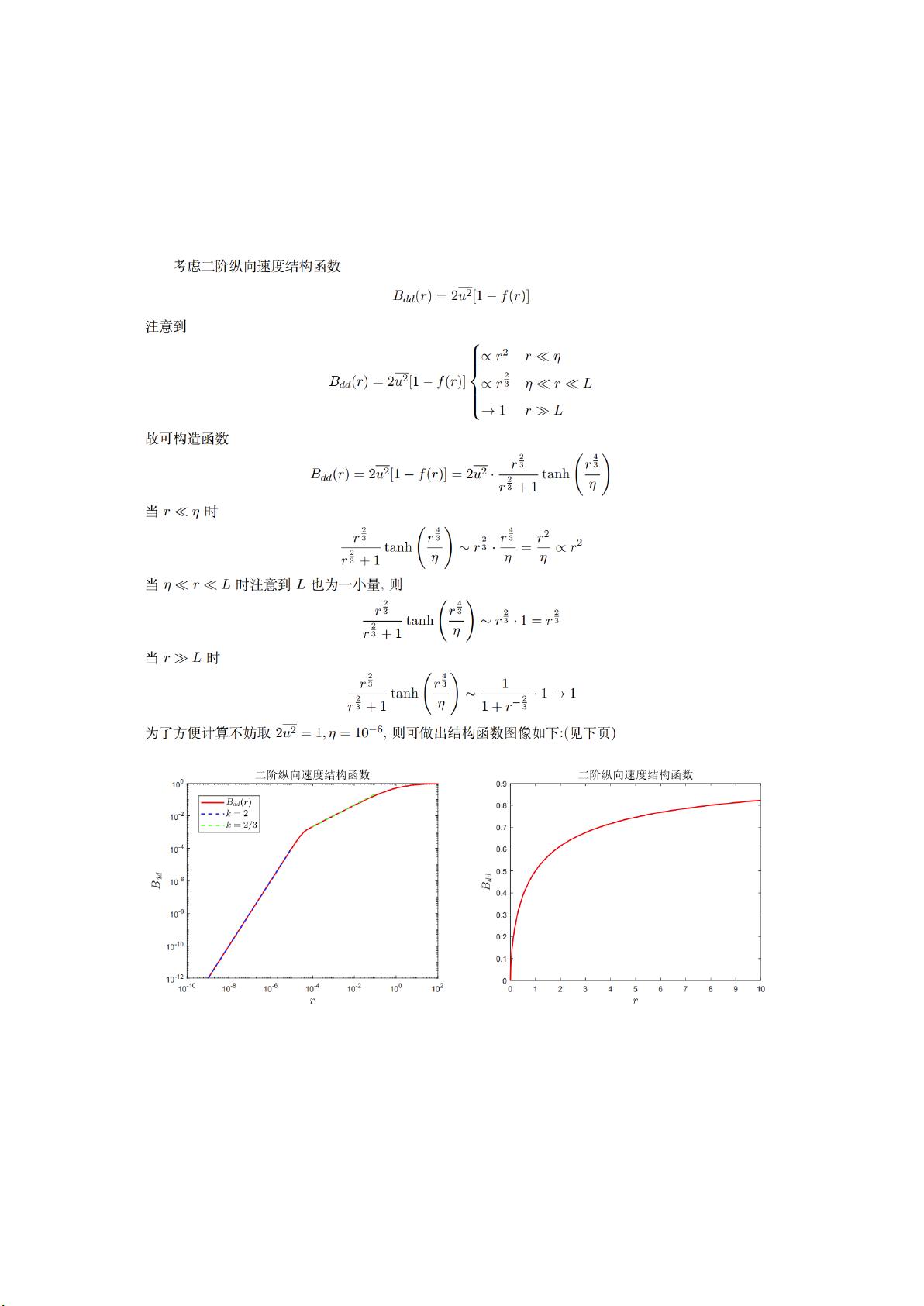
【知识点详解】 1. "2/3"定律与二阶纵向速度结构函数： "2/3"定律，也称为Kolmogorov的-2/3幂律，是湍流理论中的一个重要概念，它描述了小尺度涡旋在湍流能量耗散中的行为。在均匀各向同性湍流中，二阶纵向速度结构函数定义为两个距离为r的点之间的速度差的平均平方，即斯特列托夫函数(S2(r))。理想的"2/3"定律表示S2(r)与r的平方成正比，比例常数与平均速度平方成正比，即S2(r) ≈ C_u * r^2/3，其中C_u是一个常数。题目要求构造一个在小尺度范围内满足这一规律的结构函数，同时考虑其数学表达式的简单性和解析性。 2. Pao的能量传递模型： Pao模型是由Pao（鲍亦和）提出的，用于描述湍流能量在不同尺度间的传递过程。该模型假设能量从大尺度向小尺度以线性的方式传递，直到被小尺度涡旋耗散掉。在均匀各向同性湍流的衰减过程中，可以通过Pao模型计算无量纲的三维能谱函数，并绘制不同初始雷诺数下的能谱曲线，观察衰减规律。 3. "5/3"定律与一维能谱函数： "5/3"定律是K41理论的另一个重要部分，它涉及到一维能谱函数𝜙1(κ)。一维能谱函数是描述能量密度随波数κ分布的函数。在Kolmogorov理论中，对于小波数κ，能量谱以κ^-5/3的形式下降，这反映了湍流中小尺度涡旋的能量分布。题目中要求通过构造的结构函数计算一维能谱，并验证是否符合"5/3"定律。为了实现这一目标，通常需要进行傅里叶变换并将结构函数转换到频域。 4. She-Leveque标度律： She-Leveque层次相似律（SLHS）是针对湍流的一种非线性标度理论，它提出了一个更广泛适用的自相似假设，以解释实验数据中的非幂律行为。该理论指出，即使在非幂律的结构函数中，仍存在一种层次相似性。题目要求证明SLHS是广义扩展自相似律（GESS）的特例。GESS是一种考虑多尺度关联的自相似性方法，它允许在不同尺度上对结构函数进行扩展，从而揭示隐藏的自相似结构。证明过程涉及递推关系的建立和分析，以展示SLHS满足GESS的一般形式。 5. "-10/7"衰减规律： Kolmogorov的1941年论文中，除了著名的"2/3"定律外，还讨论了湍流动能随时间的衰减规律。在他的第二篇论文中，他提出了动量通量的衰减率约为-10/7。这个规律可以从能量守恒和湍流耗散的考虑中推导出来。对于其他衰减规律，如湍流动能的指数衰减，可以通过修改假设，例如考虑特定几何形状或边界条件的影响，理论上是可以推导出来的，但这需要对湍流动力学有深入的理解。 这些知识点涵盖了湍流理论的基本概念，包括标度律、能量传递模型、能谱函数的计算以及非线性相似理论的应用。理解和掌握这些内容对于深入研究湍流现象及其在工程和物理科学中的应用至关重要。