Lab3 崔俞崧 赵奕帆 11811305 118120111

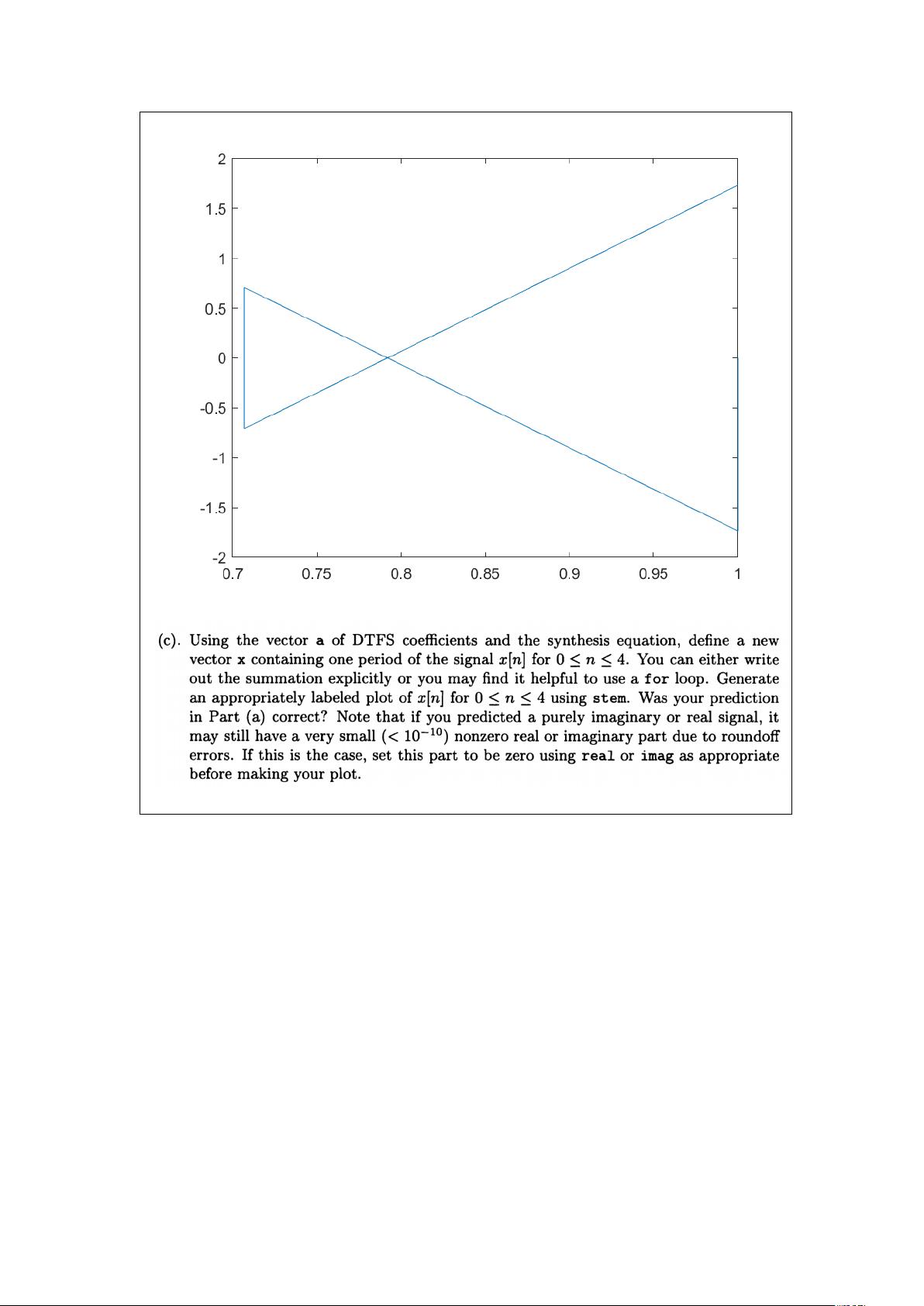
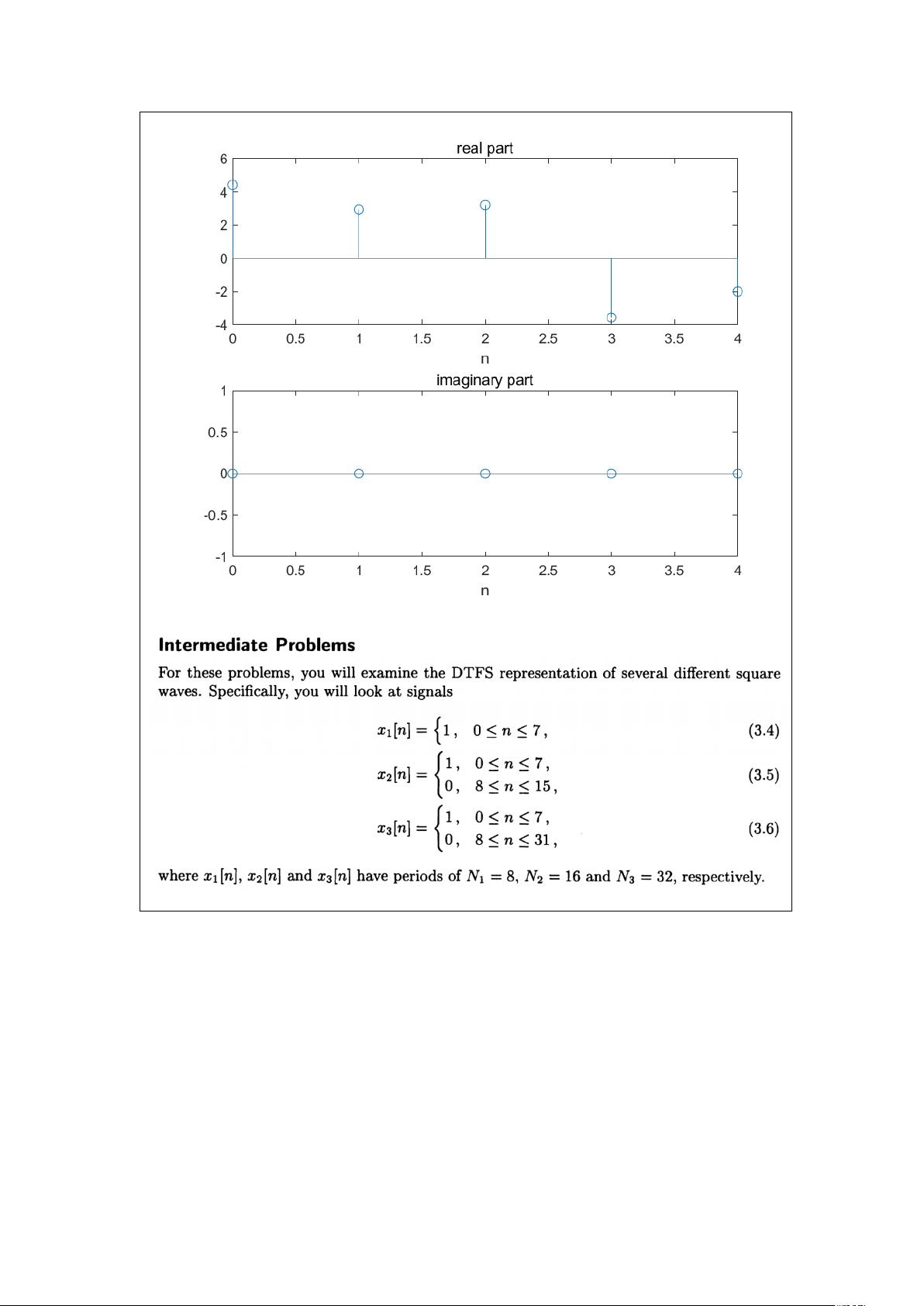
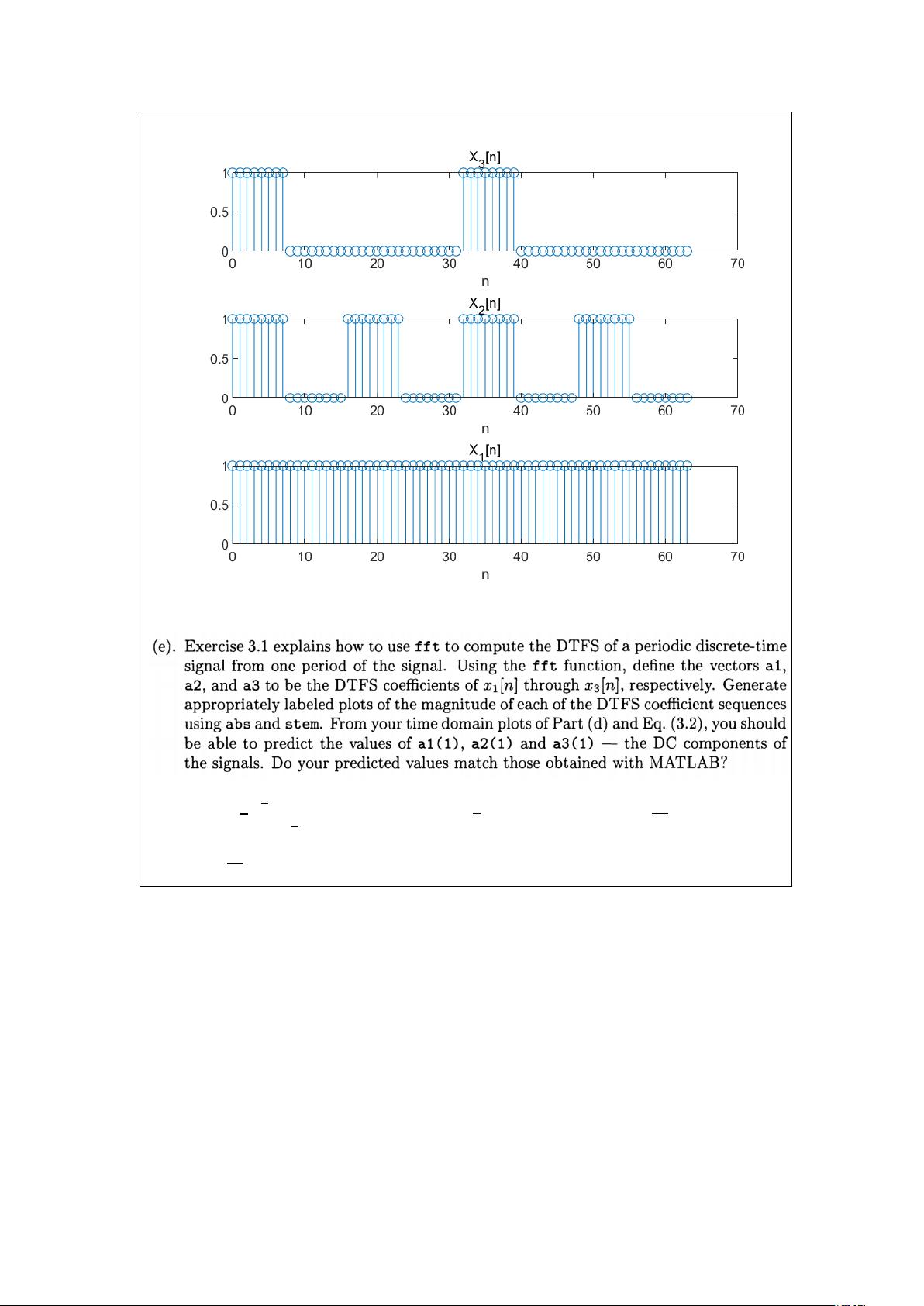
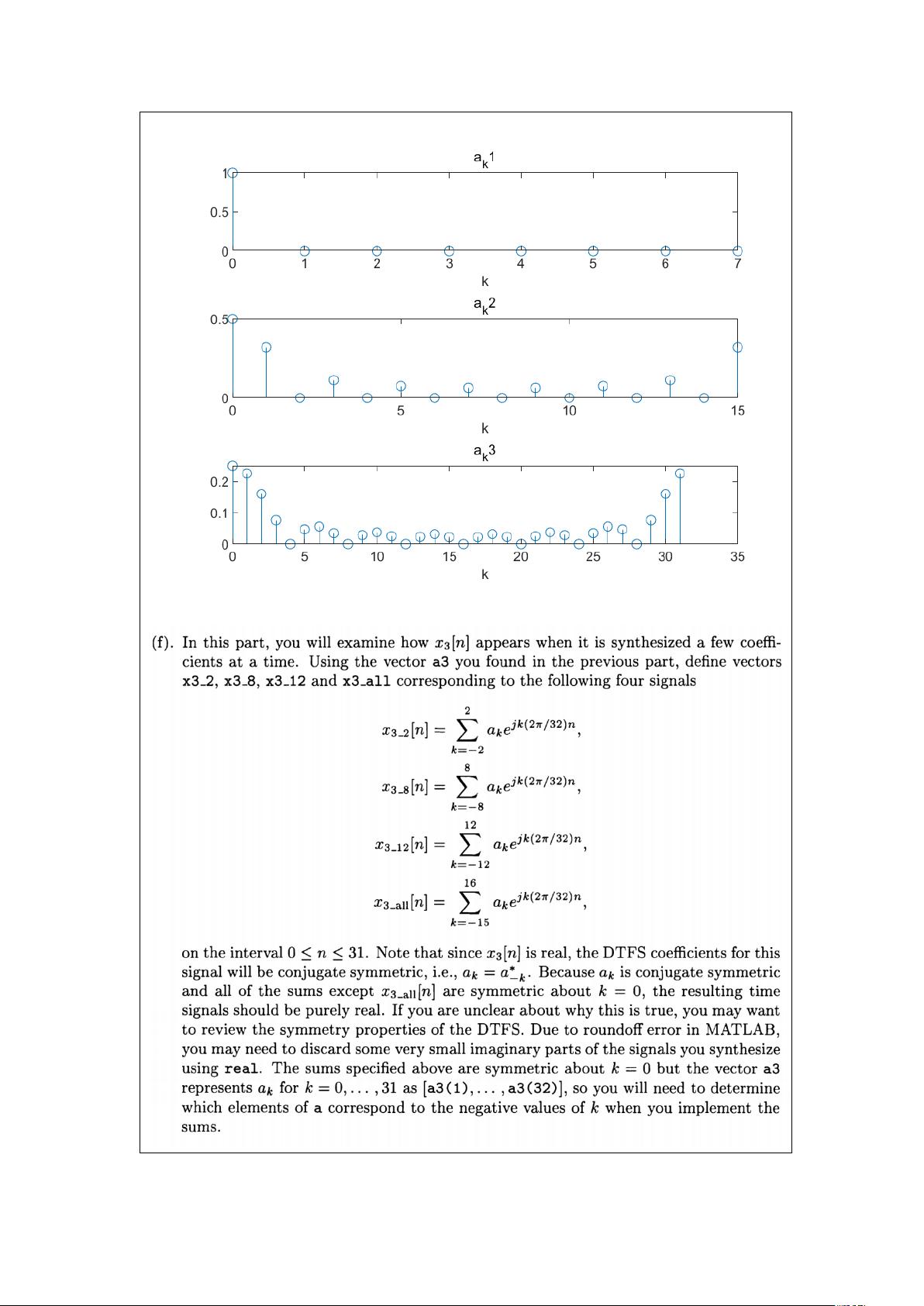
在本次实验Lab3中，主要探讨了离散时间信号的傅里叶变换（FFT）以及其在滤波器中的应用。实验由崔俞崧和赵奕帆两位同学完成，他们的学号分别是11811305和11812020。实验涉及了离散时间信号的特性、滤波效果以及FFT的计算效率优势。 1. 离散时间信号的特征与合成： 实验中的Exercise 3.5研究了离散时间信号的特征函数性质和合成。特征函数是信号的基础，它们可以用来表示信号的不同频率成分。通过合成不同幅度和相位的特征函数，可以重建原始信号。 2. 滤波器对周期性信号的影响： Exercise 3.8和3.9考察了简单滤波器对周期性离散时间和连续时间信号的效果。滤波器可以改变信号的频谱特性，例如低通滤波器会保留低频成分，而去除高频成分，从而实现信号的平滑或降噪。 3. FFT的计算效率： Exercise 3.10展示了快速傅里叶变换（FFT）相对于直接实现离散时间傅里叶级数（DTFS）的计算优势。FFT算法极大地减少了计算复杂度，使得大规模信号的频谱分析变得高效。 实验结果与分析： - 当N=5时，信号𝑥[𝑛]的傅里叶系数为：𝑎0 = 1, 𝑎1 = 2𝑒^(-𝑗π/3), 𝑎2 = 𝑒^(-𝑗π/4), 𝑎3 = 𝑒^(𝑗π/4), 𝑎4 = 2𝑒^(𝑗π/3)。其中，𝑎1, 𝑎3和𝑎4的共轭对称性表明信号𝑥[𝑛]是实数。 - 分析了𝑥1[𝑛], 𝑥2[𝑛], 和 𝑥3[𝑛]的傅里叶系数，发现随着系数数量的增加，重构的信号与原始信号更加接近。 - 在傅里叶级数合成中，观察到𝑥3_𝑎𝑙𝑙的虚部为0，进一步证实了信号𝑥[𝑛]的实数特性。 - Gibbs现象（吉布斯现象）在离散傅里叶级数近似周期函数的跳跃不连续点处表现明显，表现为高点和低点。实验中，随着参与合成的系数减少，Gibbs现象的范围更宽；反之，如果使用更多系数，由于绘图精度限制，这种现象可能难以辨识。 实验中使用的`dtfs`函数用于计算离散时间傅里叶级数，它遍历信号并对每个频率分量进行累加，然后归一化。该函数考虑了初始索引`n_init`的正负值，以确保正确地构建傅里叶系数向量。 总结来说，本次实验深入研究了离散时间信号的傅里叶变换特性，以及滤波器对信号的影响，并突显了FFT在处理大规模数据时的高效性。通过对信号的傅里叶分析，我们可以更好地理解和操纵信号的频域特性，这对于信号处理和通信系统的设计至关重要。