5. 逻辑回归(logistic regression)的本质——极大似然估计 - zjuPeco的博客 - CSDN博客1

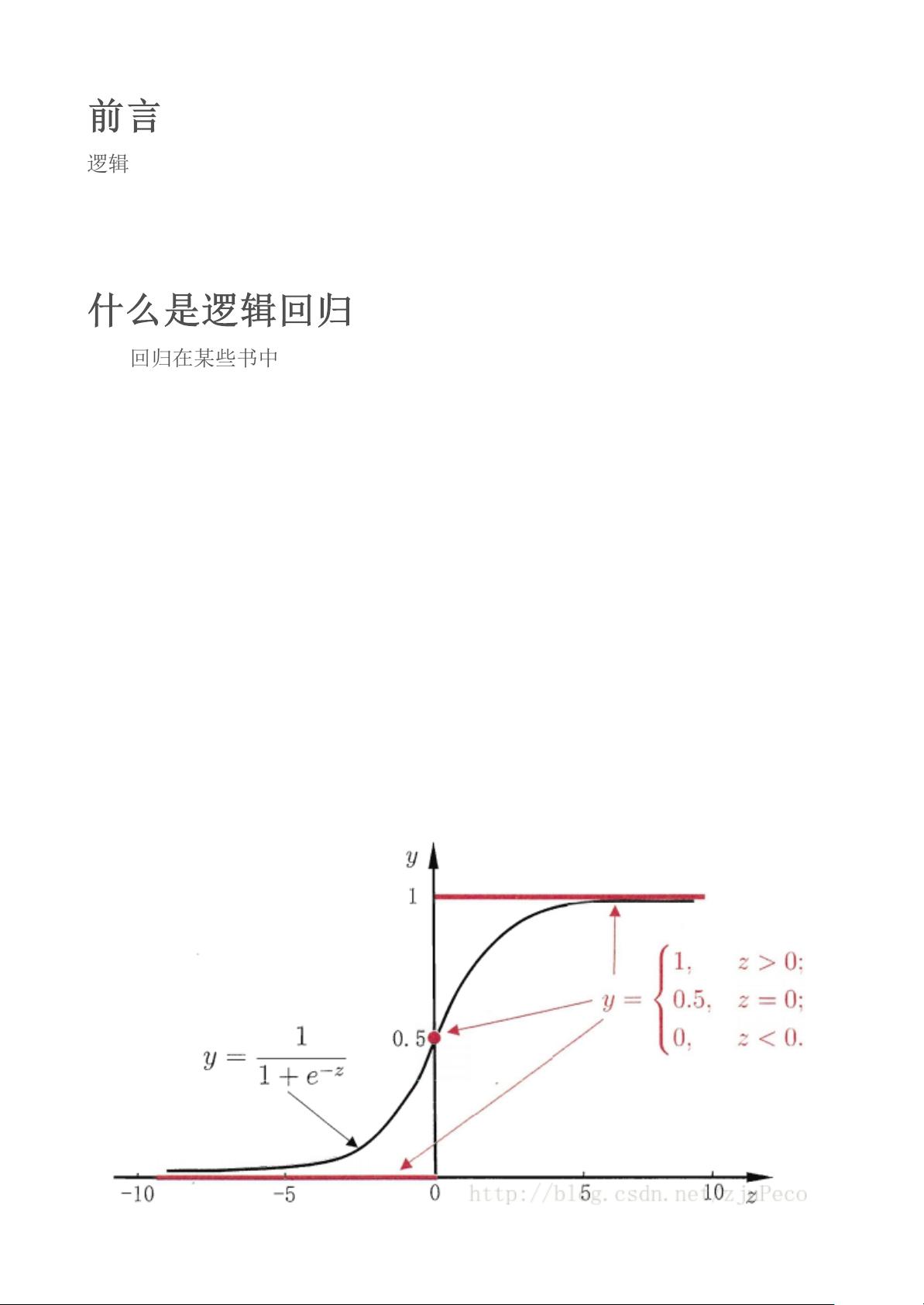
《逻辑回归(logistic regression)的本质——极大似然估计》 逻辑回归是一种广泛应用的分类方法，它虽然名字中含有“回归”，但实际上是解决分类问题的一种有效工具。逻辑回归的核心思想是通过引入Sigmoid函数，将连续的线性预测值转化为离散的类别概率。 Sigmoid函数，数学表达式为 ϕ(z) = 1 / (1 + e^(-z))，是一个在0和1之间连续且可微的S形函数。它能够将任何实数值映射到(0,1)区间，这恰好符合概率的定义。在二分类问题中，Sigmoid函数的输出可以被解释为类1的概率p(y=1|x)，而1-p(y=1|x)则为类0的概率。 逻辑回归模型的网络结构类似于自适应线性网络(Adaline)，区别在于激活函数的不同。Adaline使用线性函数y=x，而逻辑回归使用Sigmoid函数。这种差异使得逻辑回归更适合处理非线性可分的数据。 在确定模型参数w的过程中，我们通常采用极大似然估计方法。首先定义损失函数，最直观的选择是类似于线性回归的均方误差。然而，当使用Sigmoid函数时，这样的损失函数是非凸的，导致多个局部最小值，优化困难。因此，我们转而采用对数似然函数，通过取对数简化表达式： l(w) = ∑ni=1 y(i)ln(ϕ(z(i))) + (1 - y(i))ln(1 - ϕ(z(i))) 然后对l(w)取负值，得到代价函数J(w)，这样我们就可以寻找使J(w)最小的w值。这个代价函数的设计确保了，对于y=1的样本，当估计值接近1时，代价降低；对于y=0的样本，当估计值接近0时，代价同样降低。 在优化过程中，我们常使用梯度下降法更新参数w。Sigmoid函数的一个重要性质是其导数 ϕ'(z) = ϕ(z)(1 - ϕ(z))，这一特性使得我们能够在梯度下降过程中方便地计算代价函数关于w的梯度。通过迭代调整w，我们可以逐步减小代价函数，从而找到最优的模型参数。 总结来说，逻辑回归通过Sigmoid函数将连续的线性预测转换为概率，利用极大似然估计优化模型参数，并通过梯度下降法进行参数更新。这种方法不仅适用于二分类问题，还可以通过扩展处理多分类任务。逻辑回归的理论基础和实践应用使其成为机器学习领域不可或缺的一部分。