第13章1

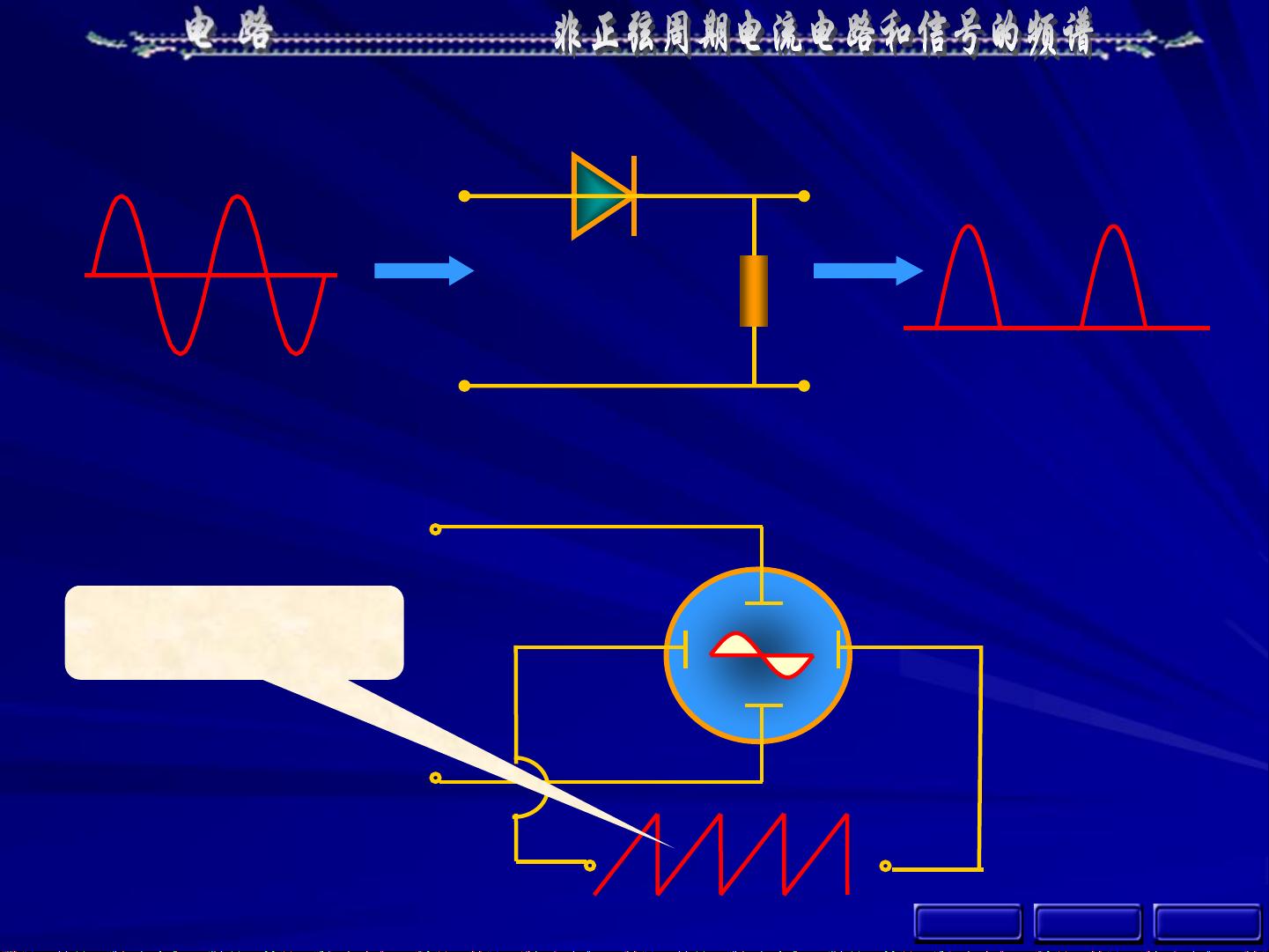
第13章主要探讨了非正弦周期电流电路的相关理论，这一章的关键点包括非正弦周期信号的分析、傅里叶级数的应用以及电路计算。在实际的电子技术、自动化、计算机和无线通信领域中，电压和电流往往不是简单的正弦波形，而是复杂的非正弦周期波形。 非正弦周期信号是指不遵循标准正弦波规律的周期性信号，它们可能呈现出如脉冲、锯齿波或半波整流等形态。例如，示波器的水平扫描电压可能是周期性的锯齿波，而半波整流电路的输出则是脉冲信号。这些信号在交、直流共存电路中也十分常见，如图例所示的脉冲电路和交直流混合电路。 非正弦周期函数可以被分解为傅里叶级数，这是数学中将复杂周期函数转化为简单正弦或余弦函数的工具。傅里叶级数的分解要求函数满足狄里赫利条件，即在一个周期内函数的极值点和间断点数量有限，且函数绝对可积。通过这种方式，非正弦周期函数可以表示为直流分量加上一系列不同频率的谐波分量。每个谐波分量由对应的系数（A0、ak、bk）和角频率（ωk）定义，系数可以通过对函数进行积分计算得出。 对于偶函数和奇函数，傅里叶级数的系数有特殊性质，这使得计算过程可以简化。周期函数的频谱图则可以展示其包含的不同频率成分的幅度和相位，这对于理解和分析非正弦信号的特性至关重要。 在电路计算中，非正弦周期电流电路的分析涉及到有效值、平均值和平均功率的概念。有效值是衡量非正弦交流电流等效于恒定直流电流的参数，平均值用于描述信号在一段时间内的平均效应，而平均功率则反映了信号在时间上的能量消耗。例如，矩形波电流可以通过傅里叶级数分解，计算其直流分量、各次谐波分量的有效值和平均功率，这对于设计和分析实际电路至关重要。 总结来说，第13章的核心内容是非正弦周期信号的傅里叶分析和其在电路计算中的应用，这些理论是理解和解决实际工程问题的基础，尤其是在电力系统、信号处理和控制系统等领域。通过深入理解非正弦周期函数的特性，工程师能够更准确地预测和控制电路的行为，从而实现更高效的设计和优化。