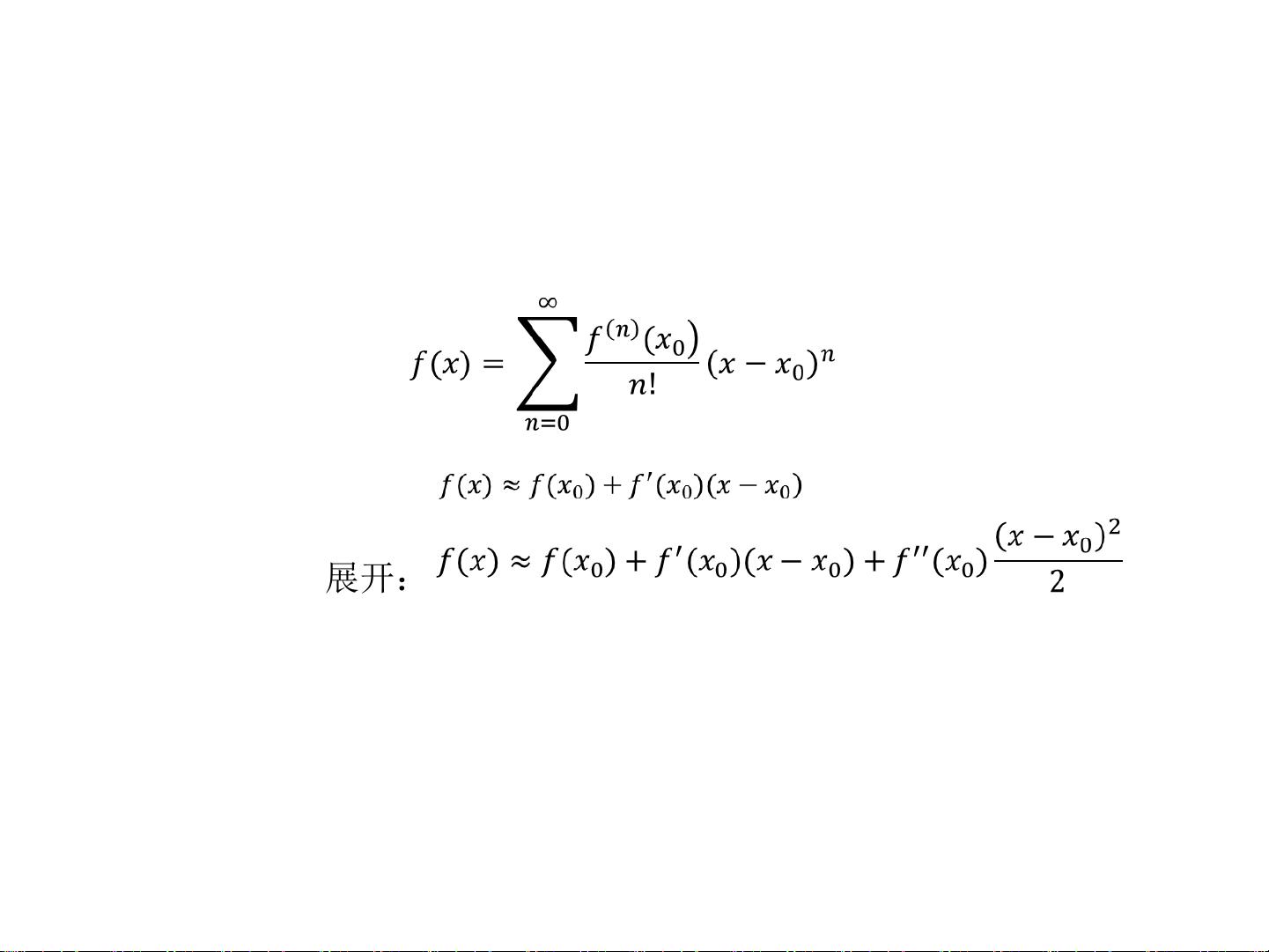GBDT_XGBoost_LGBM算法原理v1.11

《GBDT_XGBoost_LGBM算法原理v1.11》 在机器学习领域，Gradient Boosting Decision Trees (GBDT)、XGBoost和LightGBM是极具影响力的集成学习算法，它们基于梯度提升（Gradient Boosting）原理，通过构建一系列弱预测器并逐步优化来构建强大的模型。本文将深入探讨这些算法的核心概念和技术细节。 我们从基础的数学原理出发，泰勒公式是理解许多优化算法的关键。泰勒公式提供了一种将复杂函数近似为多项式的方法，这在损失函数的优化过程中起到重要作用。一阶泰勒展开用于近似函数在某一点的局部行为，而二阶泰勒展开则进一步考虑了函数的曲率，这对于梯度下降法和牛顿法的优化过程至关重要。 接下来，梯度下降法是机器学习中常见的优化算法，尤其在GBDT的实现中。它的基本思想是从一个初始点出发，沿着梯度的反方向，以一定的步长更新参数，以最小化损失函数。迭代公式可以表示为：θ_t = θ_{t-1} - α * ∇_θ L(θ)，其中θ是模型参数，L是损失函数，α是学习率。梯度下降法简单易懂，但可能收敛速度较慢，且需要合适的学习率来确保稳定收敛。 然后，牛顿法是一种利用二阶导数信息进行优化的方法，它通过构造一个二次曲面来近似损失函数，并找到这个曲面的最小值作为参数的下一个估计值。牛顿法的迭代公式是：θ_t = θ_{t-1} - [Hessian(L)]^(-1) * ∇_θ L(θ)，其中Hessian矩阵是损失函数的二阶导数，反映了函数的局部曲率。相比于梯度下降，牛顿法通常能更快地收敛，但计算Hessian矩阵可能会导致较高的计算成本。 从梯度下降法到Gradient Boosting，我们看到一个从参数空间到函数空间的转变。在GBDT中，我们不是优化单个参数，而是构建一系列决策树，每次迭代的目标是拟合上一轮残差，从而逐步减小整体误差。这种方法既利用了梯度下降的思想，又引入了模型的多样性，提高了预测性能。 XGBoost是GBDT的一种高效实现，它采用了二阶泰勒展开的近似，优化了原生GBDT的计算效率，同时引入正则化项控制模型复杂度，防止过拟合。XGBoost通过精心设计的数据结构和并行计算策略，实现了快速训练和预测，使其成为实际应用中的首选算法之一。 LightGBM进一步提升了效率，它采用梯度提升的叶子节点顺序优化（GOSS）和直方图算法，减少了内存占用和计算时间。这些优化使得LightGBM在大规模数据集上表现优异，同时保持了良好的预测精度。 GBDT、XGBoost和LightGBM是现代机器学习中不可或缺的工具，它们基于强大的数学原理和优化技术，结合了迭代学习和决策树的优势，为解决复杂问题提供了强大而高效的解决方案。在实际应用中，理解这些算法的工作原理和内在联系，对于模型的选择和调优具有极其重要的意义。