171840708_张逸凯1

在机器学习领域中，决策树算法作为一种经典的监督学习算法，被广泛应用于分类和回归任务。它通过学习简单的决策规则，对数据进行分割，以达到预测结果的目标。决策树通过递归的方式，根据特征的不同取值将数据集划分为多个子集，并且在每一个子集上，根据数据的统计特性来决定进一步的划分。学习决策树的过程，实际上就是选择最优特征和最优划分点的过程。 在这一学习过程中，决策树划分选择的标准是关键因素之一。传统的最小训练误差方法虽然简单直观，但并不是最优的选择。最小训练误差方法通过优化目标函数来减少模型对训练数据的预测误差，然而，一味追求最小化训练误差往往会导致过拟合现象的出现。过拟合是指模型在训练数据上表现非常好，但在新的、未见过的数据上表现却差强人意。过拟合现象的发生，使得模型泛化能力下降，无法在实际应用中取得良好的效果。因此，在构建决策树时，需要选择更加合适的划分标准，以平衡模型的训练误差和泛化误差。 信息增益和基尼不纯度是决策树中常用的两种划分标准。信息增益通过计算数据集划分前后的信息熵变化来评估划分的效果，基尼不纯度则是基于分类错误的概率来评估数据集的纯度。这两种标准都旨在提高数据的纯度或减少数据的不确定性，从而有助于生成对未知数据预测能力更强的决策树。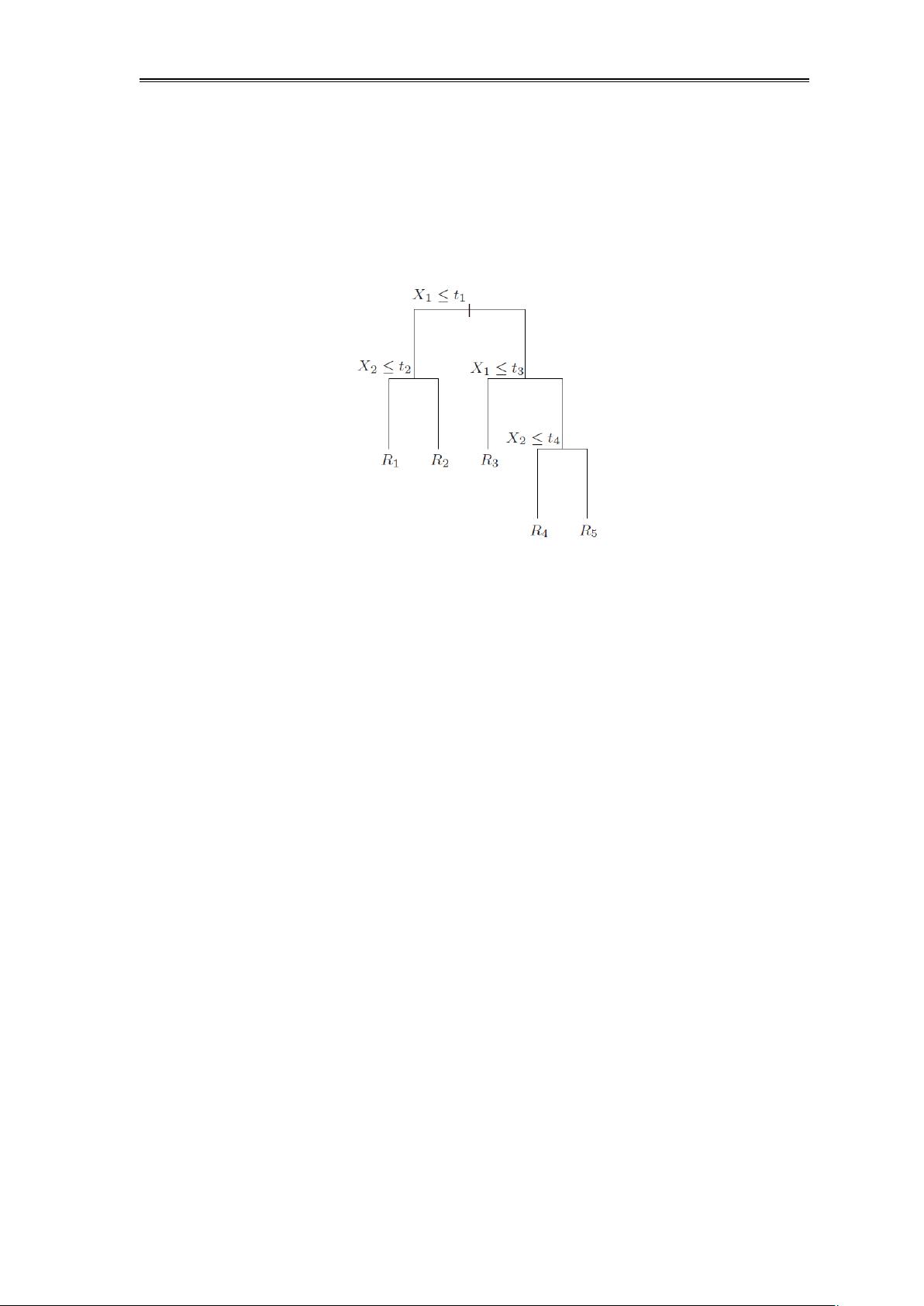 在回归任务中，回归决策树的目标是预测一个连续的数值。回归决策树可以看作是对特征空间的一种分割，它将整个特征空间划分为多个区域，并在每个区域中赋予一个固定的预测值。通过这样的方式，回归决策树实际上可以表示为一系列线性模型的组合。其数学表达式可以表示为：f(x) = ∑_{i=1}^{n} c_i I[x \in R_i]，其中c_i是每个区域R_i对应的预测值，而I[x \in R_i]是一个指示函数，该函数能够判断输入的特征向量x是否位于区域R_i中，从而返回相应的预测值c_i。 回归决策树在构建过程中同样面临着优化问题，尤其是平方误差最小化的最优划分问题。为了得到一个预测效果良好的回归决策树，需要在构建过程中，对每一个特征都尝试不同的分割点，找到能够使得划分后子集的平方误差和最小的特征和分割点。这是一个典型的贪心策略问题，通过在每一步选择最佳的特征和分割点，逐步将特征空间划分为更小的子空间，直至满足预设的停止条件，如树的深度达到某个限制值或者节点内样本数量小于某个阈值。 构建决策树的过程，涉及到学习原理的深刻理解，包括过拟合问题的认识、划分标准的选择，以及回归决策树的线性模型表示和优化问题的处理。在实际应用中，理解这些知识点对于机器学习模型的设计至关重要，特别是如何在模型复杂性和泛化能力之间找到一个合理的平衡点。只有当模型在训练集和测试集上都有良好的表现时，才能认为该模型是成功的。因此，无论是决策树的学习，还是其他机器学习模型的构建，都需要综合考虑模型的泛化能力和预测准确性，这既是对模型性能的要求，也是机器学习领域研究的热点和难点。