SA17011125+吴燕晶+概率算法1

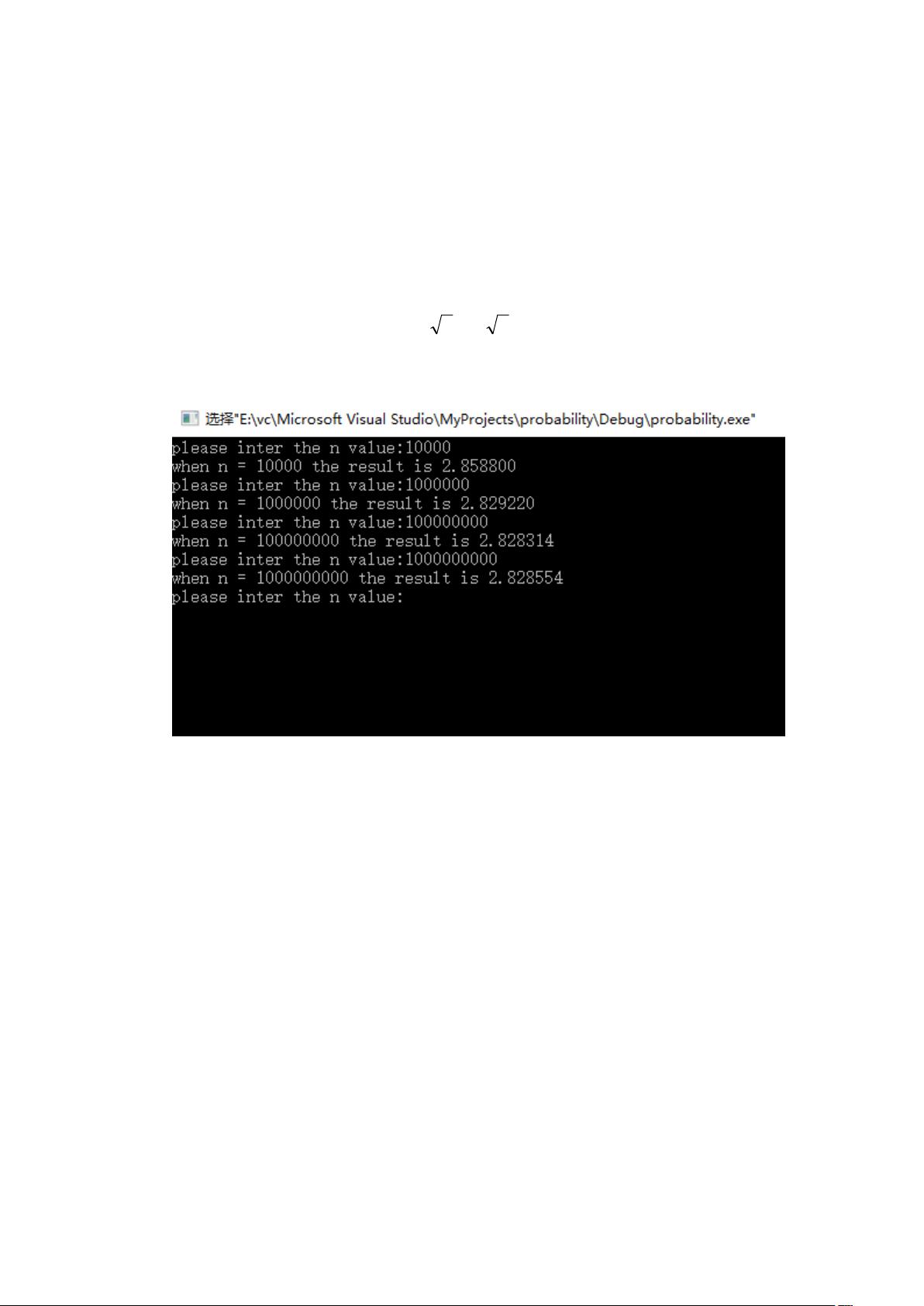
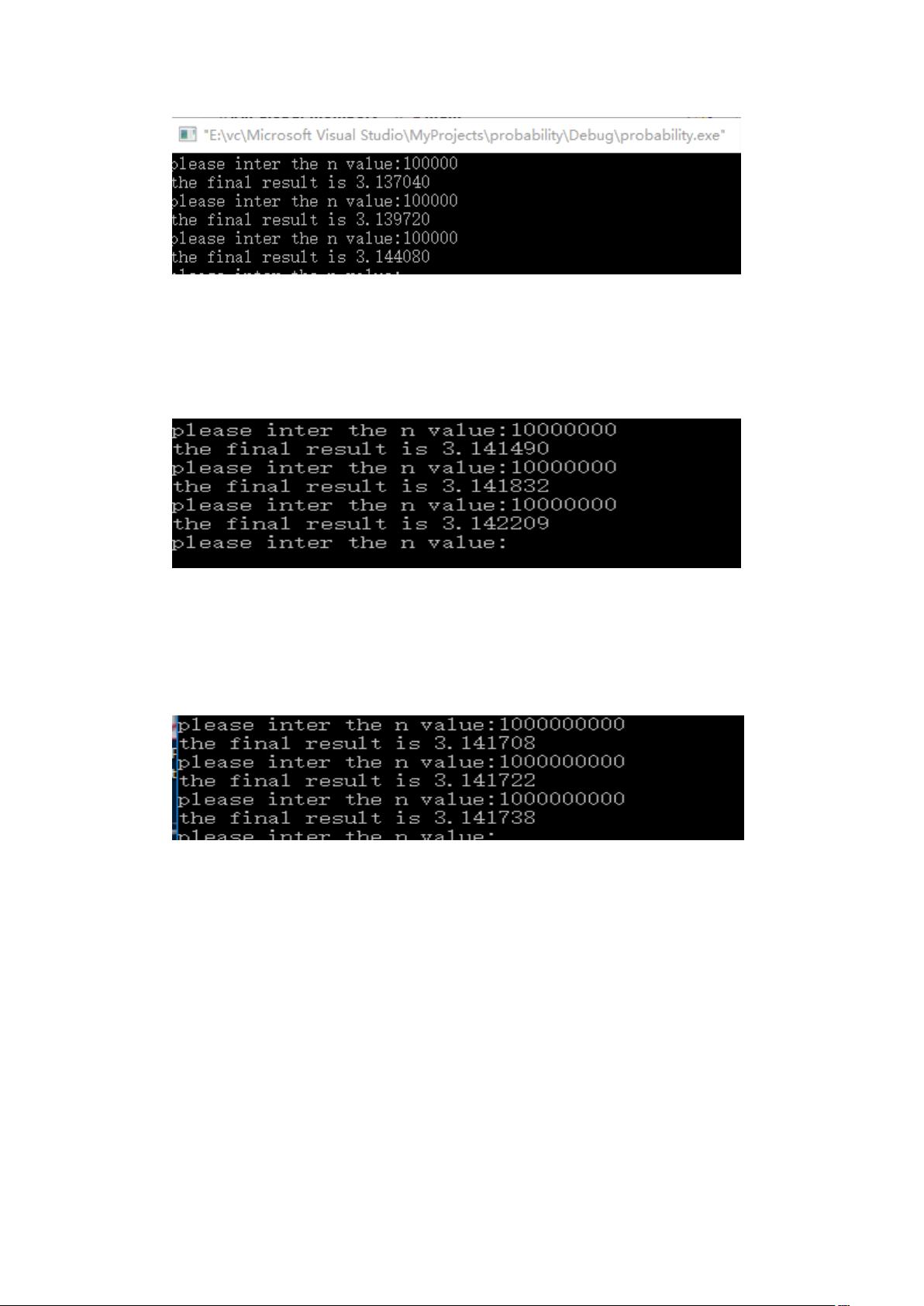
本文主要讨论了三种概率算法，用于估算数学中的特定值，包括圆周率π、函数积分以及特定线段在单位圆内的比例。这些算法基于随机数生成，并随着样本数量的增加提高精度。 我们来看Ex1，这是一个估算圆周率π的变种算法。通常的蒙特卡洛方法是通过在单位正方形内随机投掷点，然后计算落在单位圆内的点的比例来估算π。但在这个问题中，我们限定y=x，这意味着点只分布在对角线上。因此，算法现在实际上是在求解y=x在单位圆内的部分与在单位正方形内的部分之比的四倍。由于y=x在正方形内形成一个45度角的线段，其在正方形内的长度是√2，而在单位圆内该线段的长度是圆的切线，长度也是√2。因此，算法现在估算的是(√2/√2) * 4 = 4，这与π无关。 接下来是Ex2，这个例子展示了如何使用更大的样本数量（n值）来提高估算π的精度。代码中定义了一个名为`darts`的函数，它接受一个参数n，生成n个随机点，然后计算落在单位圆内的点的数量。通过比较估算值与π的真实值，我们可以看到随着n值增大，估算结果的精度也在提升。例如，当n=100000时，精度大约是1位小数；n=10000000时，精度提升到2位小数；而当n=1000000000时，精度进一步提高到3位小数。 Ex3探讨了使用概率算法来计算连续函数的积分。这里选择的函数是y = x*x，它在区间[1, 2]上的积分可以通过随机投掷点并统计落在函数下方的点的数量来估算。代码中定义了一个名为`intergrations`的函数，它接受函数指针`ft`，利用蒙特卡洛方法计算积分。函数`circle`被用作示例，但可以替换为任何其他连续函数。 总结来说，这些概率算法都是基于随机抽样和统计学原理来解决数学问题的。它们的核心思想是通过大量随机试验来逼近真实值，随着试验次数的增加，估算结果会越来越接近实际值。这种蒙特卡洛方法在解决复杂问题时具有很大的优势，因为它通常不需要复杂的数学解析，而是依赖于计算机生成大量的随机数据。