方向导数都存在。在本题中,我们讨论了几个关于方向导数和梯度的概念,并通过具体的习题解析来加深理解。 方向导数是衡量多元函数在某一特定方向上的变化率,它与偏导数密切相关。题目中提到了函数 \( z = \cos(x+y) \) 在点 \( M(0,0) \) 沿方向 \( l(3,4) \) 的方向导数。计算时,我们需要找到与 \( l \) 同向的单位向量 \( \vec{e_l} \),这里 \( \vec{e_l} = \frac{(3,4)}{\sqrt{3^2+4^2}} = \frac{(3,4)}{5} \)。接着,利用偏导数 \( \frac{\partial z}{\partial x} \) 和 \( \frac{\partial z}{\partial y} \),我们可以计算方向导数 \( \vec{e_l} \cdot (\frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}) \)。 第二部分涉及函数 \( u(x,y,z) = xyz \) 在点 \( M(1,1,1) \) 沿方向 \( l(1,1,1) \) 的方向导数。同样,我们先找到单位向量 \( \vec{e_l} \),然后利用偏导数 \( \frac{\partial u}{\partial x} \),\( \frac{\partial u}{\partial y} \),和 \( \frac{\partial u}{\partial z} \) 进行计算。 第三部分中,我们求函数 \( z = \ln(x+y) \) 在抛物线 \( y = 2 - \frac{x^2}{4} \) 上点 \( (1,2) \) 沿着切线方向的方向导数。首先找到切线的斜率,然后确定单位向量 \( \vec{e_l} \),最后计算方向导数。 第四部分则是一个综合应用,设函数 \( f(x,y) \) 在点 \( A(1,3) \) 沿不同方向的方向导数已知,要求在 \( AD \) 方向上的方向导数。通过计算沿 \( AB \) 和 \( AC \) 方向的方向导数,可以找到 \( AD \) 的单位向量,进而得到所求。 问题4展示了即使函数在某点连续且偏导数存在,沿某些特定方向的方向导数仍可能不存在。这里以函数 \( z = x^3y^3 \) 为例,证明了原点 (0,0) 沿任何非零向量 \( l(a,b) \) 的方向导数不存在。 这些习题展示了方向导数的计算方法,以及它们与偏导数、连续性和函数特性之间的关系。在实际应用中,理解并掌握这些概念对于分析多元函数的行为至关重要。
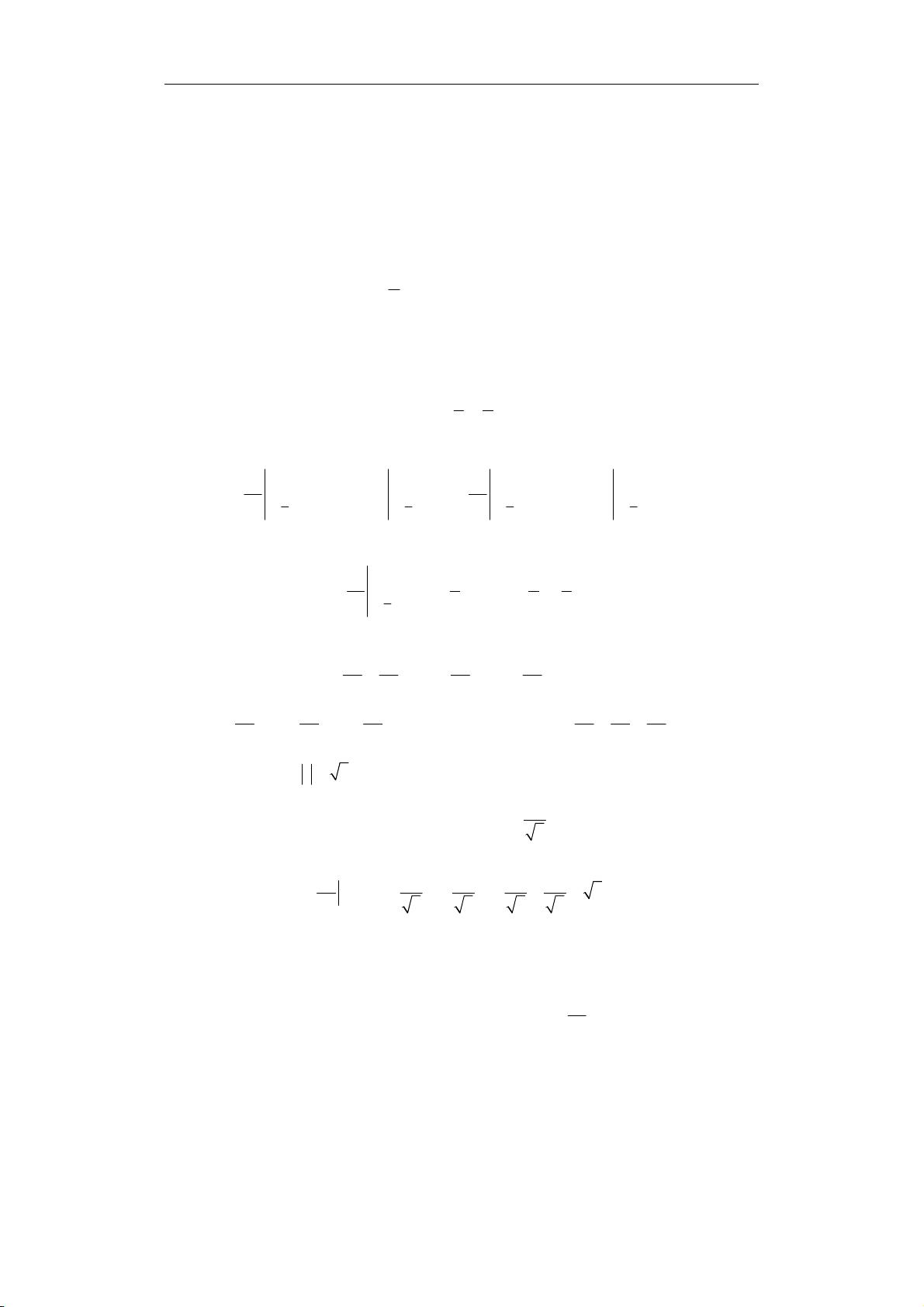
- 粉丝: 738
- 资源: 341
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜 信息提交成功
信息提交成功


评论0