非递减数列判断1

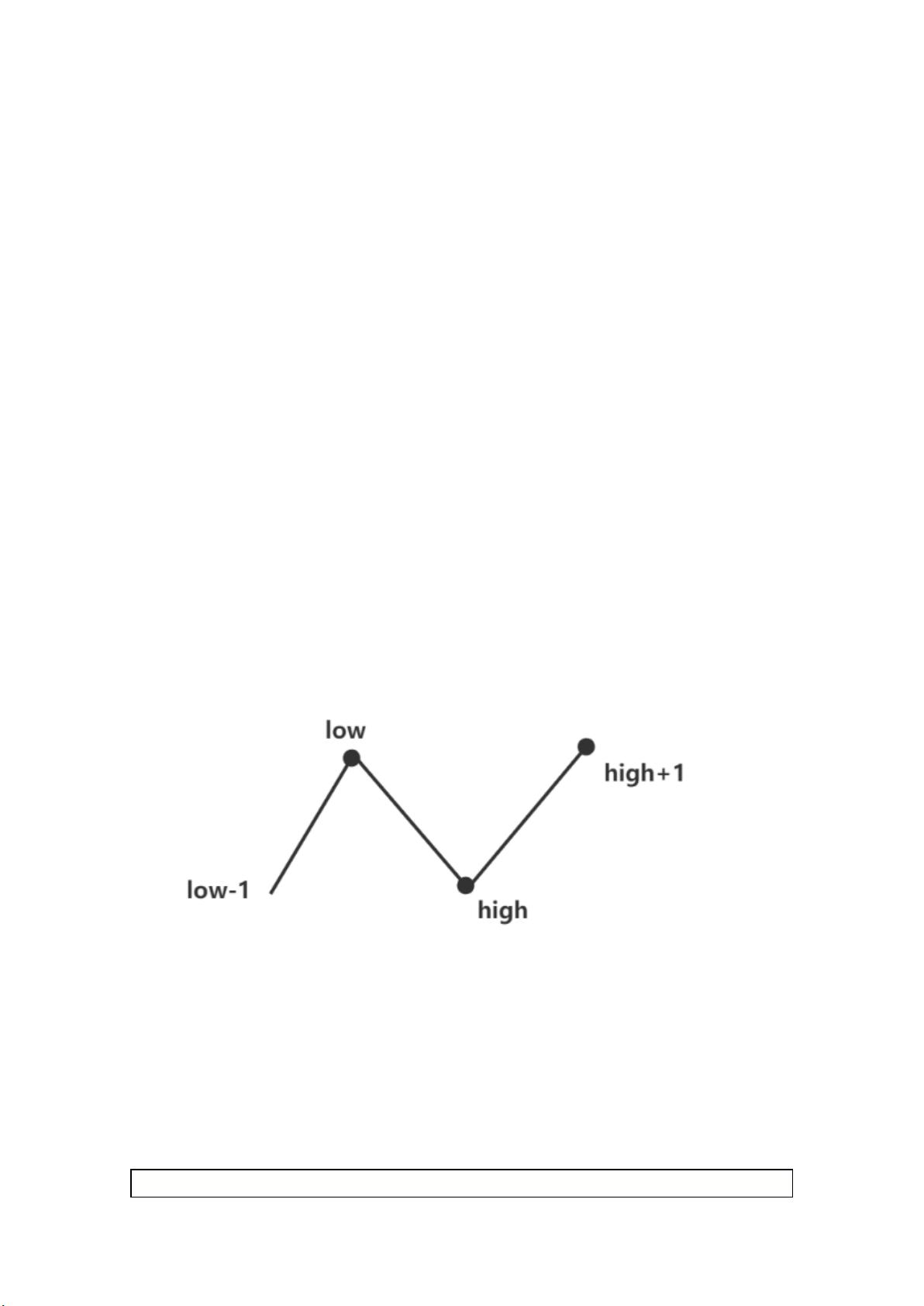
非递减数列是一个特殊的序列，其中每个元素都小于或等于其后的元素。在本题中，我们需要判断在最多改变一个元素的情况下，给定的数组是否可以转化为非递减数列。这个问题是LeetCode上的一道题目，我们可以采用双指针方法来解决。 我们需要理解题目的要求。给定一个整数数组`nums`，长度为`n`，如果在允许改变一个元素的情况下，数组可以变得非递减，那么函数应返回`true`；否则返回`false`。非递减数列的定义是对于数组中的所有`i`（0 <= i <= n-2），都满足`nums[i] <= nums[i + 1]`。 解题思路是设置两个指针，`low`和`high`，分别从数组的开头和结尾开始向中间移动。当`low`和`high`相遇时，我们检查在它们相遇的过程中是否只出现了一次失序（即相邻元素不满足非递减关系）。如果有且仅有一次失序，我们可以通过调整这个位置的元素使得数组成为非递减数列。 在移动指针的过程中，我们需要考虑以下两种情况： 1. 当`low`指针发现相邻元素失序（`nums[low] > nums[low+1]`）时，停止移动`low`，此时`low`指向的是失序的位置。 2. 当`high`指针发现相邻元素失序（`nums[high] < nums[high-1]`）时，停止移动`high`，此时`high`指向的是失序的位置。 有两种可能的调整策略： - 方案1：改变`low`位置的值，使得`nums[low-1] < nums[low] < nums[low+1]`。这需要`nums[low+1] >= nums[low-1]`。 - 方案2：改变`high`位置的值，使得`nums[high-1] < nums[high] < nums[high+1]`。这需要`nums[high+1] >= nums[high-1]`。 此外，我们还需要处理两种特殊情况： - 如果`low`指针在开始时就发现失序（`low == 0`），我们可以调整第一个元素。 - 如果`high`指针在结束时才找到失序（`high == numsSize - 1`），我们可以调整最后一个元素。 在双指针相遇后，我们检查`high - low`的差值是否小于等于1，因为一次失序可以通过改变一个元素来修正。同时，我们需要确保在失序的地方可以应用上述调整策略之一。如果满足这些条件，我们就返回`true`，表示可以调整数组为非递减数列；否则返回`false`。 以下是实现这个算法的C++代码： ```cpp bool checkPossibility(int* nums, int numsSize){ if(numsSize<=2) return true; int low=0; int high=numsSize-1; while(low<high){ while(low<high&&nums[low]<=nums[low+1]) low++; while(low<high&&nums[high]>=nums[high-1]) high--; if((high-low)<=1&&(low==0||high==numsSize-1||nums[low+1]>=nums[low-1]||nums[high-1]<=nums[high+1])) return true; } return false; } ``` 这个算法的时间复杂度是O(n)，因为我们至多遍历整个数组一次。空间复杂度是O(1)，因为我们只需要常数级别的额外空间。通过这种方法，我们能够有效地判断给定数组在改变一个元素后是否能成为非递减数列。