第06章--回溯法1-新1

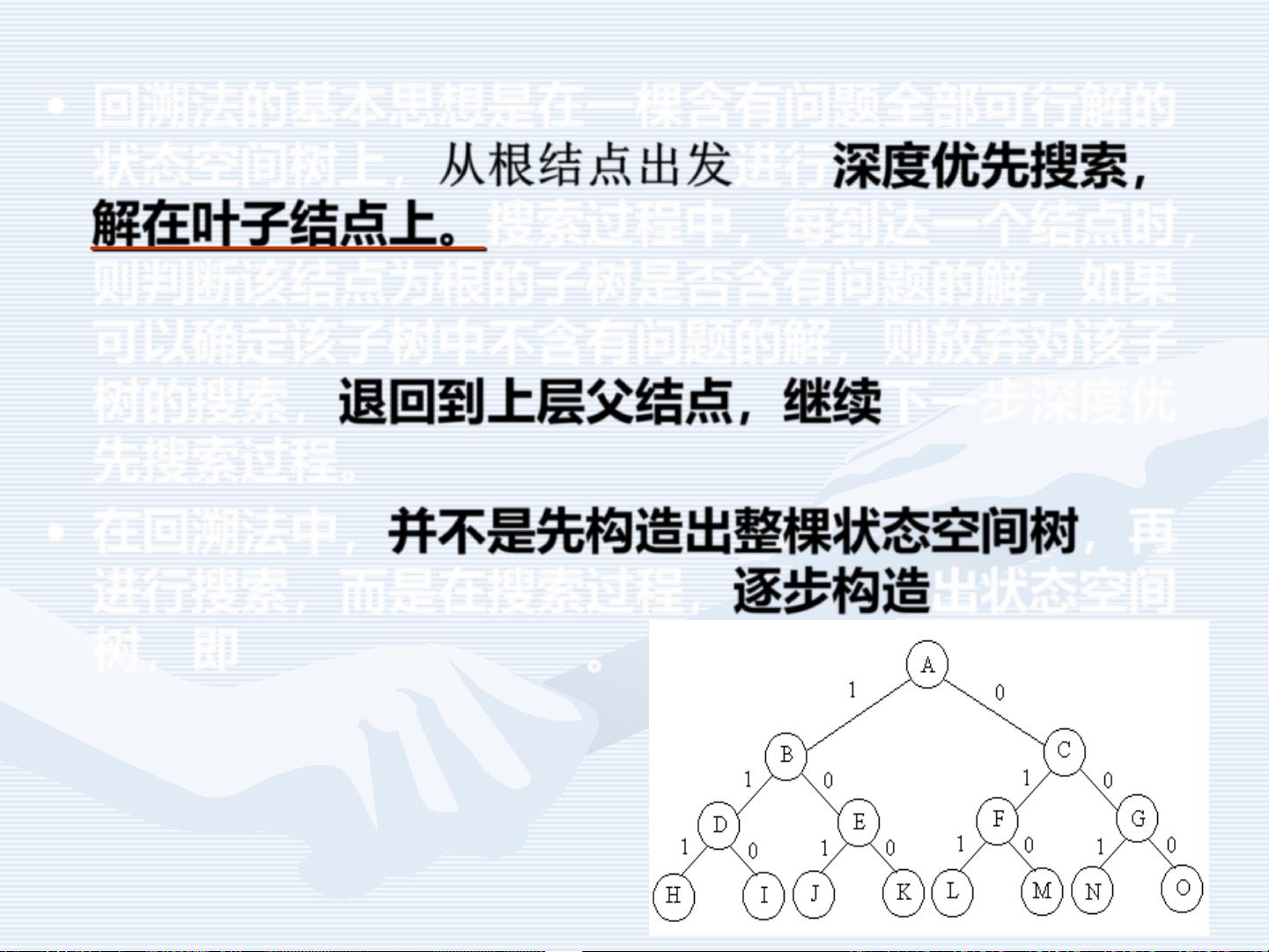
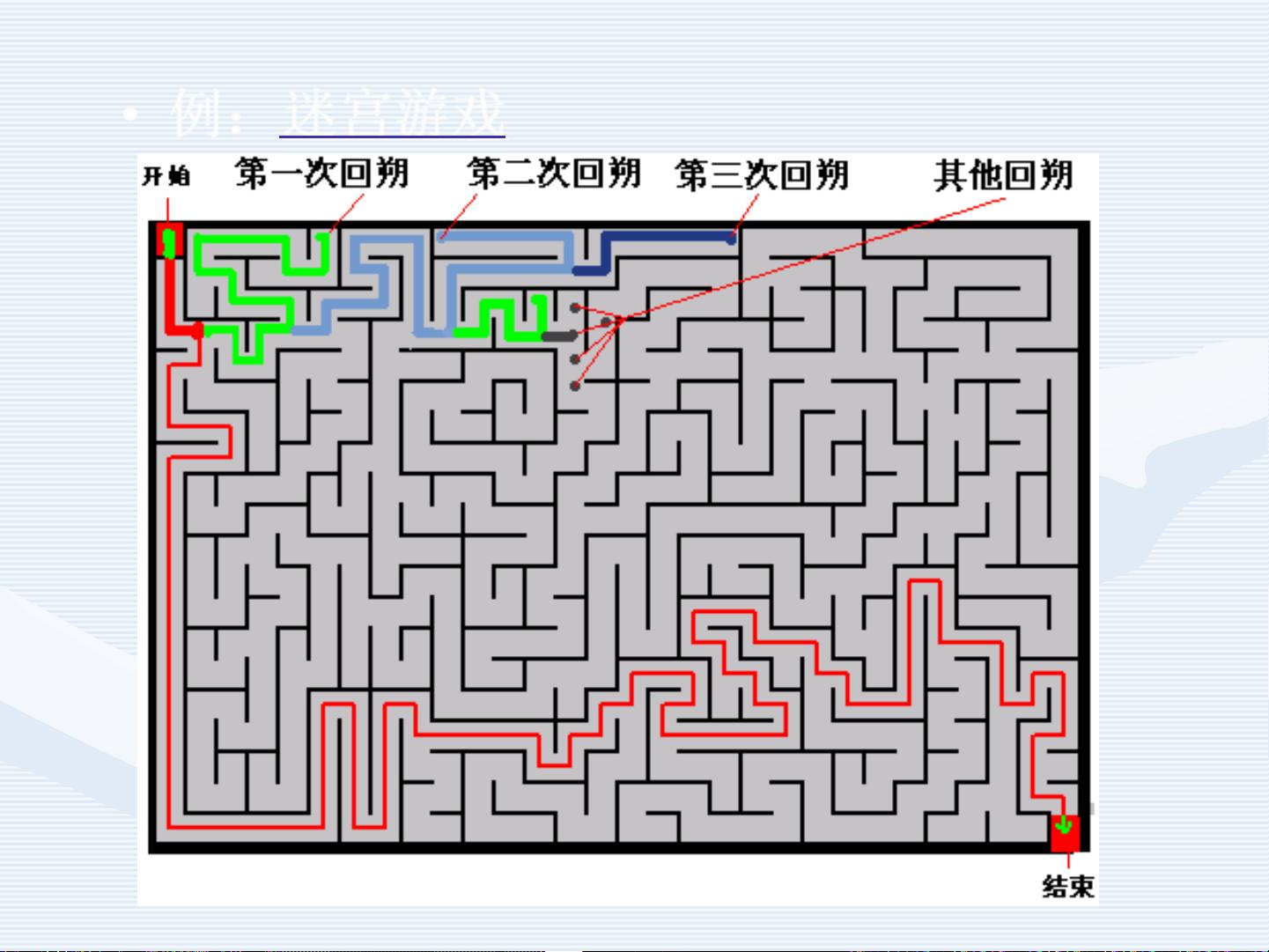
回溯法是一种基于深度优先搜索的算法，常用于解决那些具有大量组合可能性的问题，如棋盘游戏、逻辑谜题和优化问题。它被称作“通用的解题法”，因为其适用范围广泛，能处理多种类型的问题。在回溯法中，我们构建一个问题的状态空间树，其中每个节点代表问题的一个可能状态，而从根节点到叶子节点的路径对应问题的一个决策序列。 解空间是所有可能决策序列的集合，其中满足特定约束条件的序列被称为可行解。在最优解的情况下，我们需要找到在约束条件下使目标函数达到最优的可行解。回溯法通过深度优先搜索策略来遍历状态空间树，从根节点开始，逐步构造和搜索树的分支。 在搜索过程中，回溯法会判断当前节点（子树）是否包含问题的解。如果确定当前子树不可能包含解，算法就会回溯到父节点，继续搜索其他分支，这一过程称为剪枝。剪枝通过使用限界函数和约束函数来实现，前者用于避免生成非最优解，后者确保当前决策符合问题的规则和限制。 回溯法的步骤大致如下： 1. 定义问题的解空间，通常以一个n元组表示，每个元素xi来自有限集合Si。 2. 设计一种方法来组织解空间，使其便于深度优先搜索。 3. 从根节点开始，递归地探索每个节点，每次增加一个决策（xi），并测试是否满足约束和限界函数。 4. 如果当前选择的决策导致无法得到最优解或违反约束，就撤销这个决策（回溯），尝试下一个可能的决策。 5. 当到达叶子节点且满足所有条件时，找到了一个可能的解，继续搜索直至找到所有解或达到预设的停止条件。 回溯法的特点之一是它不会一次性构建完整的状态空间树，而是边搜索边构造，从而节省了存储空间。如果从根节点到叶子节点的最长路径长度为h(n)，回溯法通常需要O(h(n))的空间复杂度，而显式存储整个解空间可能需要O(2^h(n))或O(h(n)!). 回溯法的应用实例包括但不限于： 1. 8皇后问题：在8x8的棋盘上放置8个皇后，使得任意两个皇后之间不能在同一行、同一列或同一对角线上。 2. 子集和数问题：找出一个集合的所有子集，使得子集的元素之和等于特定数值。 3. 图的着色问题：给定一张图，用最少的颜色给各个顶点涂色，使得相邻的顶点颜色不同。 回溯法是一种强大的算法，它通过有选择地搜索解空间来避免不必要的计算，从而有效地解决复杂的组合优化问题。在实际应用中，理解和熟练掌握回溯法及其剪枝策略是至关重要的。