算法设计与分析第六章1

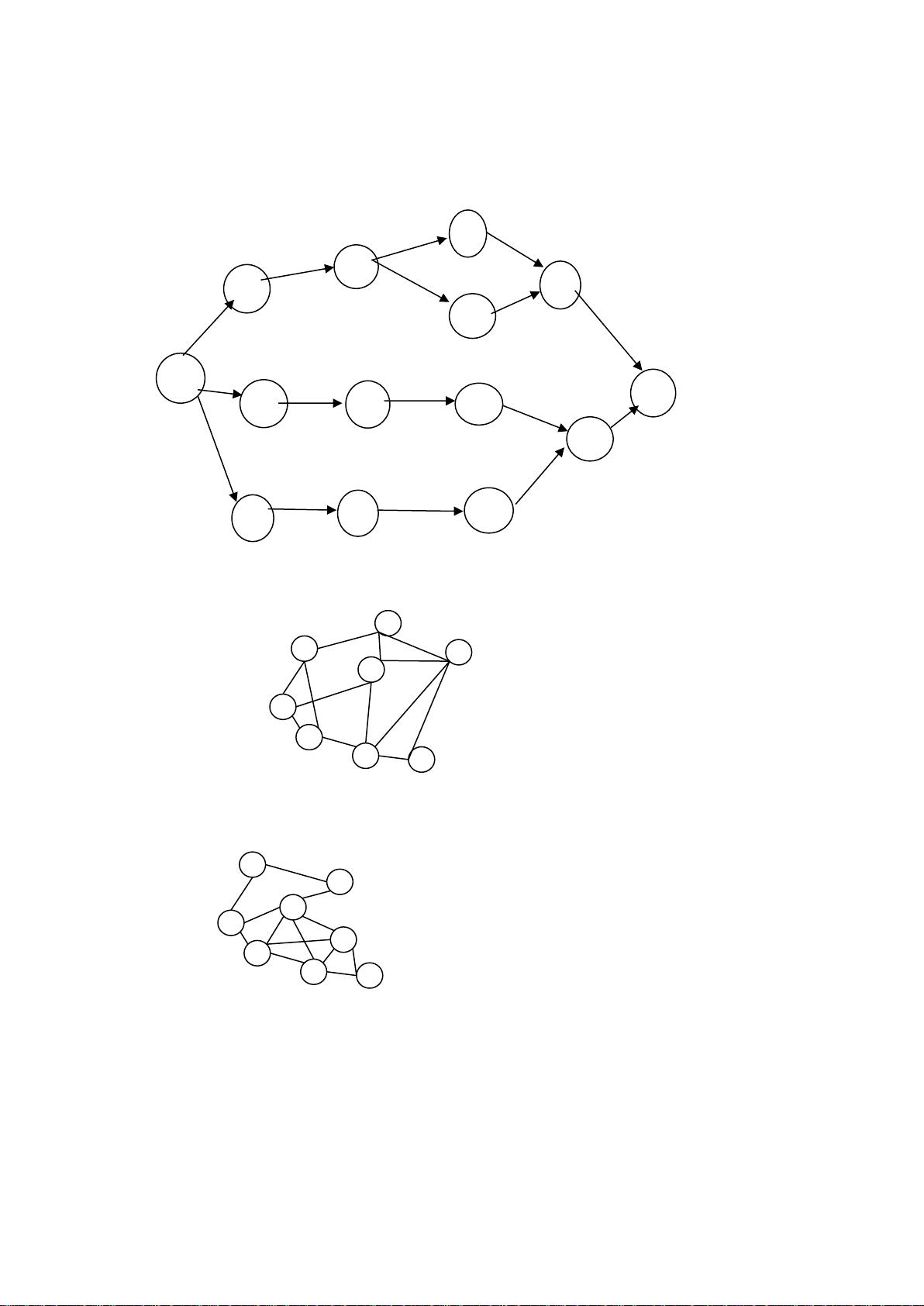
算法设计与分析是计算机科学中的核心课程，涵盖了各种算法的设计策略、分析方法和优化技巧。本部分的内容主要涉及搜索算法、图论问题、最优化问题和特定应用算法的解决。 1. **搜索算法**： - **Best-first搜索**：通常指的是基于节点评估函数的搜索策略，它不一定比爬山法更高效，效率取决于评估函数的质量。 - **深度优先搜索(DFS)**：使用栈来存储待访问节点，不使用堆或队列，时间复杂性与广度优先搜索(BFS)相比，在某些情况下可能更高。 2. **爬山法与分支界限法**： - **爬山法**：通过局部优化逐步接近全局最优解，适用于连续优化问题。 - **分支界限法**：用于离散优化问题，通过剪枝避免无效搜索，通常能更快找到全局最优解。 3. **广度优先搜索(BFS)求最短路径**：在无权图中，BFS可以找到两点间的最短路径，如果路径中有负权边，则不适用。违反条件的例子：如果存在负权边，可能导致在没有遍历完整个图的情况下找到的不是最短路径。 4. **国际象棋马的跳跃问题**：马在棋盘上的移动符合L型规则，从一个位置到另一个位置的步数可以通过模拟马的跳跃来计算。 5. **气球游戏**：通过数学分析，可以找出唯一能获得特定得分的组合，从而判断获胜者。 6. **装载问题**：这是一个经典的二维背包问题，可以通过动态规划或贪心策略解决。 7. **爬山法与分支界限法找最短路径**：爬山法会从一个起点逐步优化到达目标，而分支界限法则通过系统化地展开搜索树并剪枝来找到最优解。 8. **哈密顿路的搜索**：使用深度优先搜索或回溯法来判断图中是否存在一条通过所有顶点的路径。 9. **最大完全子图(团)**：寻找图中最大的完全子图，可以使用染色或搜索算法来解决。 10. **分支界限法求最短路径**：通过构建搜索树，每次扩展节点时更新路径成本，并使用限界函数进行剪枝。 11. **哈密尔顿环的分支界限法**：寻找最小代价的哈密尔顿环，需要构造合适的限界函数和搜索策略，确保在剪枝过程中保留最优解。 12. **Sticks问题**：这是一道恢复序列的问题，可以使用贪心算法或回溯法，通过比较所有可能的组合找到最小长度。 13. **分数分解**：这是一个组合优化问题，可以通过动态规划或回溯法找到满足条件的不同解集个数。 14. **埃及分数**：寻找给定分数的最优分解，涉及贪心策略和回溯算法，以最小的加数个数和最大的最小加数为目标。 以上各点都是算法设计与分析中的重要概念，理解和掌握这些知识点对于解决实际问题至关重要。在学习过程中，结合具体的实例和练习，可以更好地加深理解并提高解决问题的能力。