没有合适的资源?快使用搜索试试~ 我知道了~
2019期刊-可控性综述1

试读
25页
需积分: 0 0 下载量 155 浏览量
更新于2022-08-04
收藏 1.8MB PDF 举报
在过去的十年里,网络控制性的研究呈现出爆发式增长。这篇综述文章主要关注网络线性动态系统的可控性,探讨了网络拓扑结构、节点系统动力学、外部控制输入以及内部动力学相互作用如何影响这些复杂网络动态系统的可控性。文章评估了分析网络可控性的不同方法,并讨论了一些关于驱动节点选择、网络可控性优化和控制能量的高级主题。同时,还介绍了这些理论在现实世界网络系统中的潜在应用,并对未来的研究前景进行了展望。
一、引言
可控性是控制理论中的基本概念之一,它量化了一个动态系统从任意初始状态到任意目标状态的能力,可以在有限时间内完成这一过程。这一概念不仅在系统工程和控制技术中有着广泛的应用,而且在化学与物流过程、核反应堆、电力系统、航空航天工程,以及近年来的量子系统和纳米技术等领域也发挥着重要作用。
传统的控制理论中的可控性概念主要关注单个但维度较高的系统的内在动力学。然而,在大数据时代和万物互联的世界里,这种传统理论已无法满足需求。网络可控性研究则将注意力转向了更复杂的网络系统,其中包含了多个相互连接的动态子系统。
二、网络可控性的基本概念
网络可控性涉及网络结构与系统动力学的相互作用。一个网络可以被视为由多个节点(每个代表一个动态系统)和连接它们的边(代表节点之间的相互作用)组成。网络的可控性取决于以下几个关键因素:
1. **网络拓扑**:网络的连接方式对其可控性有重大影响。例如,全连通网络通常比部分连接的网络更容易控制。
2. **节点系统动力学**:每个节点的动力学特性决定了网络的可控性。不同的节点可能有不同的动力学行为,这会影响整个网络的可控性。
3. **外部控制输入**:通过网络中的某些节点施加控制输入可以改变整个系统的状态。选择哪些节点作为控制输入的源(称为驱动节点)是网络可控性研究的一个重要方面。
4. **内部动力学交互**:节点之间的相互作用也是影响网络可控性的关键因素。这些相互作用可能促进或阻碍控制信号在整个网络中的传播。
三、网络可控性分析方法
分析网络可控性的方法多种多样,包括但不限于计算格拉姆矩阵、利用特征值分析、以及基于图论的方法。这些方法可以帮助识别网络的可控性状态,以及找到最小数量的驱动节点以实现对整个网络的控制。
四、驱动节点选择和网络可控性优化
选择合适的驱动节点对于提高网络的可控性和降低控制成本至关重要。有些算法致力于最小化驱动节点的数量,而另一些则寻求优化控制能量的使用。这些优化问题通常与网络的结构和节点动力学紧密相关。
五、控制能量与网络性能
控制能量是实现网络状态转移所需的总能量。优化控制策略不仅可以减少能源消耗,还可以改善网络的整体性能。例如,通过精心设计控制输入的时间序列和幅度,可以降低控制能量,从而实现高效且经济的网络控制。
六、现实世界应用与未来展望
网络可控性的理论已经应用于各种实际系统,如电力网络的调度、交通网络的流量控制、生物网络的调节等。随着网络科学的不断发展,预计未来的研究将更深入地探讨网络的动态特性,开发出更高效、更具适应性的控制策略,并进一步探索网络可控性在新兴领域的应用,如物联网、智能城市和多智能体系统。
总结来说,网络可控性的研究涵盖了从理论分析到实际应用的广阔领域,为理解和控制复杂网络系统提供了强大的工具。随着科技的不断进步,网络可控性将继续成为控制理论和工程领域的重要研究方向。

8 IEEE CIRCUITS AND SYSTEMS MAGAZINE 1531-636X/19©2019IEEE SECOND QUARTER 2019
Featu re
©ISTOCKPHOTO.COM/BLACKJACK3D
The last decade has seen an explosion of research in net-
work controllability. The present article reviews some basic
concepts, significant progress, important results and recent
advances in the studies of the controllability of networked
linear dynamical systems, regarding the relationship of the
network topology, node-system dynamics, external control
inputs and inner dynamical interactions with the controllabil-
ity of such complex networked dynamical systems. Different
approaches to analyzing the network controllability are evalu-
ated. Some advanced topics on the selection of driver nodes,
optimization of network controllability and control energy are
discussed. Potential applications to real-world networked sys-
tems are also described. Finally, a near-future research out-
look is highlighted.
1. Introduction
C
ontrollability, as one of the fundamental con-
cepts in control theory, quantifies the ability
to steer a dynamical system from an arbitrary
initial state to an arbitrary terminal state in finite time
[1], [2]. In general, controllability is a prerequisite of
control actions. Many important applications have
been found, not only in systems engineering and con-
trol technology, but also in such areas as chemical and
logistics processes, nuclear reactors, power systems,
aerospace engineering and recently quantum systems
and nanotechnology.
The classical notion of controllability in control the-
ory focuses on the inherent dynamics of a single albeit
higher-dimensional system. In the big-data era and omni-
networking world today, the traditional control theory
Abs tract
Advances in Network
Controllability
Linying Xiang, Fei Chen, Wei Ren, and Guanrong Chen
Digital Object Identifier 10.1109/MCAS.2019.2909446
Date of publication: 20 May 2019
Authorized licensed use limited to: Qingdao University. Downloaded on October 23,2020 at 05:30:51 UTC from IEEE Xplore. Restrictions apply.

SECOND QUARTER 2019 IEEE CIRCUITS AND SYSTEMS MAGAZINE 9
is encountered more and more large-scale complex
networks [3]–[7], where nodes are higher-dimensional
dynamical systems and edges represent the interactions
among them. Typical examples include the Internet,
WWW, wireless communication networks, transpor-
tation networks, power grids, sensor networks, brain
neural networks, metabolic networks, gene regulatory
networks, social networks, and many others. Develop-
ments in engineering, physics and biology have recently
extended the classic concepts and notions on systems
control to networks control. It has been noted that per-
turbations on one node in a network can influence and
alter the states of many other nodes through their local
interactions. This interconnectedness can be exploited
to effectively control a complex network by manipulat-
ing the states of only a small fraction of nodes, in which
the underlying network structure plays a crucial role.
Therefore, it is of theoretical and practical importance
to explore the controllability of complex networked sys-
tems from a network-theoretic perspective. This can
help better understand, predict and optimize the collec-
tive behaviors of various networked dynamical systems
in practical applications.
In the past decade, research on network controlla-
bility has attracted increasing attention and, in effect,
become an exciting and rapidly developing research
direction. The goal of this article is to survey on the
current flourishing advances in the studies of the con-
trollability of networked linear dynamical systems.
Fundamental concepts and selected theoretical results
on both state controllability and structural controlla-
bility for different types of complex networked systems
are reviewed and discussed. Several specific applica-
tions of network controllability are described. Finally,
a near-future research outlook will be highlighted.
2. Notions of Network Controllability
In the present literature, there are several notions of
network controllability, which strongly depend on the
types of the networked control systems and the forms of
admissible control inputs, but they can be classified into
two essential types of state controllability and structur-
al controllability in general.
2.1 State Controllability
The basic concept of (complete) state controllability was
introduced by Kalman in the 1960s [1], for a linear time-
invariant (LTI) dynamical system of the form
() () ()xt AxtBut
00
=+
o
(1)
where
() [(), (),, ()]xt xtxt xt R
n
Tn
12
f != is the internal
state vector of the system at time
,t
() [(), (),,ut utut
12
f=
()]ut R
m
Tm
! is the input vector at time
,t
A R
nn
0
!
#
is
the system matrix and
B
R
nm
0
!
#
is the input matrix.
Definition 1
The LTI system (1) is said to be (completely) state con-
trollable if, for any initial state
()xt
R
n
0
! and any final
state
() ,xt R
f
n
! there exist a finite time
t
1
and an input
() ,[,],ut ttt
R
m
01
!! such that
(; (),) ().xt xt uxt
f10
=
This definition implies that any initial state
()
xt
0
can
be steered to any final state
()xt
f
in finite time. Here, the
finite time
t
1
is not fixed, the trajectory of the dynamical
system (1) between
t
0
and
t
1
is not specified, and there
is no constraint on the input vector
().ut
The classic algebraic controllability criteria are given
as follows [2].
Theorem 1 (State Controllability Theorem)
The LTI system (1) is completely state controllable (state
controllable, or simply, controllable) if and only if one of
the following conditions is satisfied:
i) the controllability matrix
[, ,, ]QBAB
AB
n
000
0
1
0
f=
-
(2)
has full row rank; that is,
() .rank
Qn
= (3)
ii)
[,
].
,rank sI AB nsC
n 00
6 !-=
iii) the relationship
A
TT
0
ymy
= implies ,B 0
T
0
!y
where
y
is the nonzero left eigenvector of
A
0
associated
with the eigenvalue
.m
iv) the Gramian matrix
WeBB
ed
t
c
At
t
t
T
At
0
0
T
0
0
1
0
=
#
(4)
is nonsingular.
Conditions (i), (ii), (iii) and (iv) in Theorem 1 are re-
ferred to as the Kalman rank criterion, Popov-Belevitch-
Hautus (PBH) rank criterion, PBH eigenvector test, and
Gramian matrix criterion, respectively. They are equiva-
lent for the LTI system (1).
Today, strongly stimulated by the rapid and promis-
ing development of network science and engineering,
Linying Xiang and Fei Chen are with the School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, P. R. China,
(e-mails: xianglinying@neuq.edu.cn; xianglyhk@gmail.com). Fei Chen is also with the State Key Laboratory of Synthetical Automation for Process In-
dustries, Northeastern University, Shenyang 110004, P. R. China. Wei Ren is with the Department of Electrical and Computer Engineering, University of
California, Riverside, CA 92521, USA, Guanrong Chen is with the Department of Electronic Engineering, City University of Hong Kong, Kowloon, Hong
Kong SAR, P. R. China.
Authorized licensed use limited to: Qingdao University. Downloaded on October 23,2020 at 05:30:51 UTC from IEEE Xplore. Restrictions apply.

10 IEEE CIRCUITS AND SYSTEMS MAGAZINE SECOND QUARTER 2019
the concept of state controllability of an LTI system has
been extended to a complex network of many such sys-
tems interconnected together. The latter focuses on the
effects of the interactions among the multiple systems
on the collective dynamics of the whole network.
To introduce this notion, consider a set of one-
dimensional LTI control systems,
() ()xt ax t
ii
jj
j
N
1
=+
=
o
/
(),bu t
im m
m
M
1=
/
,, , ,iN12
f= and form a network by these
systems as nodes, altogether described by
() () (),xt Ax tBut=+
o
(5)
where
() [(), (),, ()]xt xtxt xt R
N
TN
12
f != is the state
vector of all nodes at time
,t
in which
()xt
i
can represent
the opinion of a person in a social network or the posi-
tion of a sensor in a mobile sensor network;
() [(),ut ut
1
=
(),, ()]ut ut R
M
TM
2
f ! is the input vector, in which
()ut
i
can represent the command of a leader in a social net-
work or the message signal of a device in a sensor net-
work;
()Bb R
im
NM
!=
#
is the input matrix identifying
the nodes that are being directly controlled, in which
b
im
represents the strength of an external control sig-
nal
()ut
m
imposed on node
;i
()Aa R
ij
NN
!=
#
is the ad-
jacency matrix of the underlying network, in which the
element
a 0
ij
! (usually,
)a 0
ij
2
denotes the weight of a
directed edge
(,)ji
from node
j
to node
i
(for an un-
directed network,
),
aa
ij ji
= for all
,i
,, , .
jN
12f= The
overall networked system described by (5) can be de-
noted by the matrix pair
(, ).AB
The concept of state controllability for the above-
described linear network can be analogously defined,
as follows.
Definition 2
The linear network (5) is said to be state controllable
if, for any initial state
()xt R
N
0
! and any final state
() ,xt R
f
N
! there exist a finite time
t
1
and an input
() ,ut R
M
!
[, ],ttt
01
! such that
(; (),) ().xt xt uxt
f10
=
The aforementioned Kalman rank criterion suggests
that the networked system (5) is state controllable if and
only if the controllability matrix
[, ,, ]QBAB
AB
N 1
f=
-
is of full row rank, i.e.,
() .rank QN
= This can be eas-
ily tested for lower-dimensional systems, namely with
a small
,N
but is very difficult to verify for large-scale
and complex-structured networks. Moreover, to numeri-
cally check this rank condition, one has to know the ex-
act parameter values in matrices
A
and
.B
In practice,
system parameter values may vary or never be known
precisely due to noise or measuring errors. For example,
for a gene regulatory network, one does not have any
method today to estimate the edge weights, only know-
ing whether or not there is an edge. Hence, it is hard to
numerically verify the Kalman rank condition assuming
known and fixed edge weights. In addition, this rank cri-
terion does not show how to find an appropriate
B
for
a given
A
so as to satisfy the required full-rank condi-
tion. These situations had led to very few applications
in large-sized complex networked systems, motivating
the introduction of the following concept of structural
controllability for networked systems.
2.2 Structural Controllability
Structural control theory, firstly introduced by Lin in
1974 [8], offers a more comprehensive framework to
avoid the above-mentioned limitations of the Kalman
rank criterion. This concept emphasizes the crucial
role of the underlying network structure in determin-
ing the state controllability, where the matrices
A
and
B
are both parameterized but preserving the system
structure. An LTI system
(, )AB is a structured system
if the entries in
A
and
B
are either fixed zeros, which
reflect the fixed un-connecting sub-structure of the
network, or independent nonzero parameters, which
reflect the variable edge weights of the network. More
precisely, a fixed zero indicates the absence of a rela-
tion between some state variables of nodes, while a
nonzero parameter characterizes the relationship
between two corresponding state variables. The two
matrices
A
and
B
are called structured matrices. A
structured system can represent a large class of lin-
ear systems since its nonzero parameters can vary, but
the connecting structure of the system has been de-
termined by the locations of those fixed zeros, which
cannot be changed.
To a structured system, one can associate it with a
digraph whose nodes denote the (state and input) vari-
ables and edges indicate the connections between some
variables [8]. Using this type of representation, one can
investigate system properties from a graph-theoretic
perspective. More precisely, a structured system
(, )AB
can be represented by a digraph
(, )(,)GABVE
= with
VV V
AB
'
= being the node set and EE E
AB
'= being the
edge set. Here,
{, ,, }{,,,}Vxxxvv v
AN N12 12
ff==
is the
set of state nodes, corresponding to the
N
nodes in the
original network
()GA
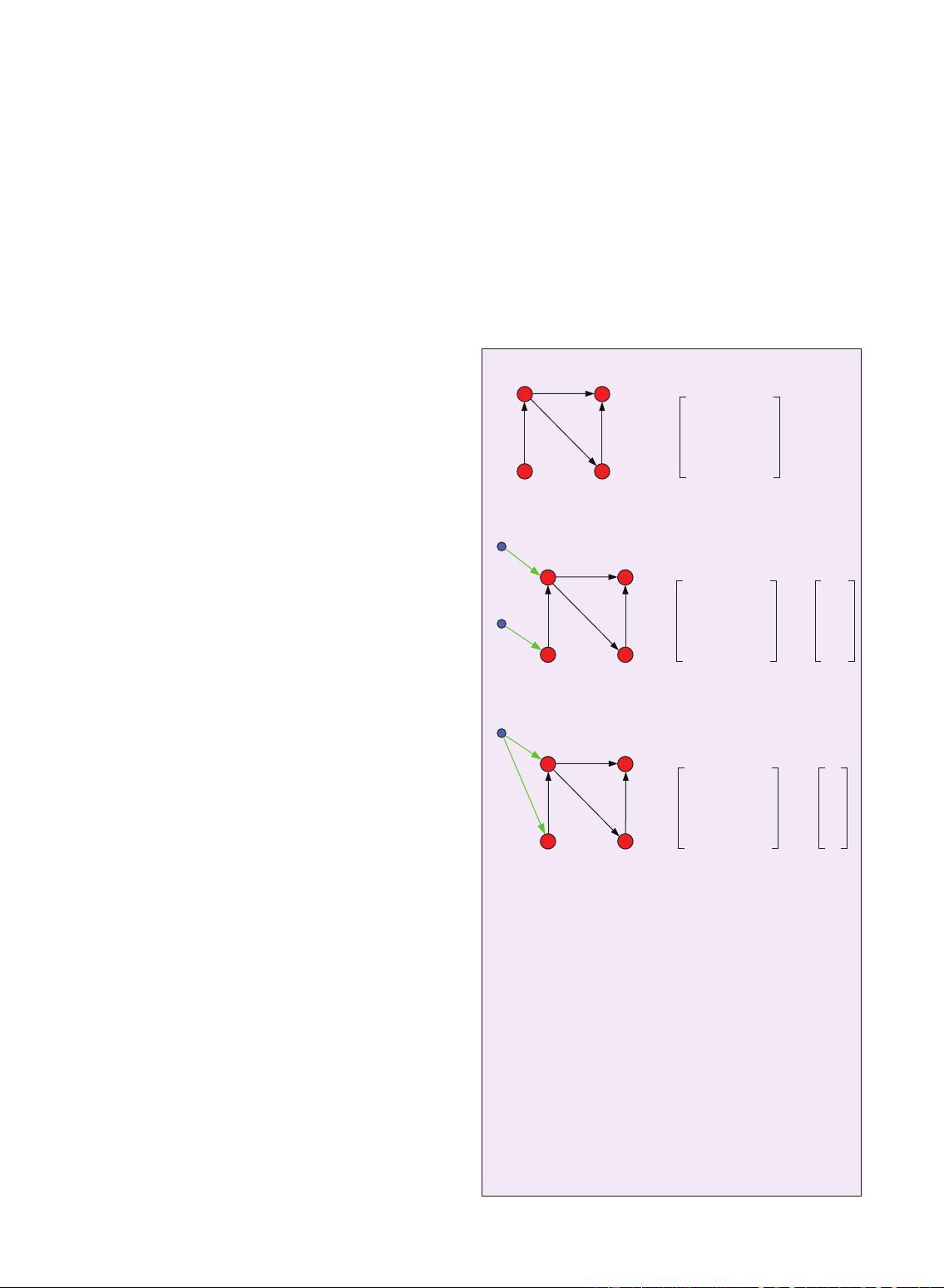
(e.g. the nodes in Fig. 1(a) marked
by red);
{, ,, }{ ,,,}Vuuu vv v
BMNN
NM
12 12
ff
==
++ +
is the
set of input nodes corresponding to the
M
inputs (e.g. the
nodes in Fig. 1(b) marked by blue);
{( ,) }Exxa 0
Ajiij
!;=
is the set of edges between state nodes (e.g. the edges
in Fig. 1(b) marked by black);
{( ,) }Euxb 0
Bmiim
!;= is
the set of edges between input nodes and state nodes
(e.g. the edges in Fig. 1(b) marked by green). Note that
the system matrix
A
is the weighted adjacency matrix
of the original network. The state nodes connected to
some input nodes are called controlled nodes (e.g.
x
1
and
x
2
in Figs. 1(b) and (c)). Denoting the number of
Authorized licensed use limited to: Qingdao University. Downloaded on October 23,2020 at 05:30:51 UTC from IEEE Xplore. Restrictions apply.
SECOND QUARTER 2019 IEEE CIRCUITS AND SYSTEMS MAGAZINE 11
controlled nodes as
,M
l
one has
MM$
l
because one in-
put node can be connected to multiple state nodes (see
Fig. 1(c), where a single input node
u
1
is simultaneously
connected to two state nodes
x
1
and
).x
2
Those con-
trolled nodes that do not share input nodes are called
driver nodes (e.g.,
x
1
and
x
2
in Fig. 1(b)). Obviously, the
number of driver nodes is equal to the number of inde-
pendent inputs.
A state node
x
i
is inaccessible if there are no directed
paths reaching
x
i
from the input nodes (see Fig. 2(a)).
The digraph
(, )GAB contains a dilation if there is a sub-
set of nodes
SV
A
1 such that their common-neighbor
set of
,S denoted as
()
,TS has fewer nodes than
S
itself
(see Fig. 2(b)). Here,
()TS
is the set of nodes
,v
j
in which
there is a directed edge from
v
j
to some other node in
.S
Note that the input nodes are not allowed to belong
to
S
but may belong to
()
.TS For a digraph, a sequence
of oriented edges
(, ),vv
jj1+
,, ,,jk12 1
f
=-
where the
nodes
{, ,,}vv v
k12
f are distinct, is called a simple di-
rected path. When
v
k
coincides with
,v
1
the sequence
of edges is called a simple directed cycle. For a digraph
(, ),GAB
one can define the following subgraphs (see
Fig. 2(c)):
i) a stem is a simple directed path originating from
an input node;
ii) a bud is a simple directed cycle with an additional
edge that ends at, but does not begin from, a node
of the directed cycle;
iii) a cactus is defined recursively: Start with a stem,
which is a cactus. Let
,C
a
O
and
e
be respectively
a cactus, a simple directed cycle that is disjoint
with
,C
a
and an additional directed edge that con-
nects
C
a
to
O
in
(, ).GAB Then,
{}CeO
a
''
is also
a cactus. After all,
(, )GAB
is spanned by cacti if
there exists a set of disjoint cacti that cover all
state nodes.
Definition 3
An LTI system (, )AB is structurally controllable if one
can set some values to the nonzero parameters in
A
and
B
such that the resulting system is state controllable in
the sense of Kalman defined in Definition 2 above.
Note that cactus is the minimum structure containing
no inaccessible nodes and no dilations. In other words,
for a given cactus, the removal of any edge will lead to
either inaccessibility or dilation.
A simple and elegant necessary and sufficient condi-
tion for the structural controllability of a system can be
given by simply inspecting its topology [8], [9].
Theorem 2 (Structural Controllability Theorem)
An LTI system
(, )AB
is structurally controllable if and
only if
i) the digraph (, )GAB contains no inaccessible nodes
and no dilations; or
ii) the digraph (, )GAB is spanned by cacti.
Note that, differing from the Kalman algebraic (rank)
condition, this theorem offers a geometric (graphical)
condition. Note also that if a system is structurally
controllable then it is state controllable for most pos-
sible parameter realizations, except perhaps for some
improperly related ones in the parameter space. There-
fore, structural controllability is a generic property of
Figure 1. Graphical representation of a linear networked
system
(, ).AB (a) The original network without external con-
trol input. All nodes in the network are called state nodes,
where the state node set is
{,
,,}
.V xxxx
A
1234
= The state ma-
trix
A
denotes the weighted wiring diagram of the digraph
()
.GA (b) The network is controlled by two input nodes,
where the input node set is
{, }.Vuu
B
12
= The input matrix
B
identifies the state nodes
{, }
xx
12
that are controlled by
the input
() [(), ()]ut utut
T
12
= with two independent signals
()ut
1
and
(),
ut
2
respectively. Therefore, both
x
1
and
x
2
are
driver nodes. (c) The network is controlled by a single input
node, where the input node set is
{}
.
Vu
B 1
=
u
The input matrix
B
u
identifies the state nodes
{, }
xx
12
that are controlled by
the same input signal
()
()
ut
ut
1
= with different control gains
b
1
and
.b
2
Here, if
x
2
is chosen to be a driver node then
x
1
cannot be so, because they share the same input node
.u
1
x
1
x
2
x
3
x
2
x
3
x
4
x
1
x
4
a
41
a
41
a
43
a
43
a
31
a
31
a
12
a
12
000
0000
00
a
43
0
00
A =
a
41
a
31
a
12
Original Network G(A)
Controlled Network G(A, B)
b
1
b
2
u
1
u
2
x
2
x
3
x
1
x
4
a
41
a
43
a
31
a
12
b
1
b
2
u
1
000
0000
00
a
43
0
00
A = B =
a
41
a
31
a
12
b
1
0 b
2
0
0
0
0
0
x = Ax
.
x
= Ax + Bu
.
,
000
0000
00
a
43
0
00
A = B =
a
41
a
31
a
12
b
1
b
2
0
0
,
~
Controlled Network G(A, B)
~
x
= Ax + Bu
.
~
(a)
(b)
(c)
Authorized licensed use limited to: Qingdao University. Downloaded on October 23,2020 at 05:30:51 UTC from IEEE Xplore. Restrictions apply.
剩余24页未读,继续阅读
查看更多
资源推荐
资源评论
103 浏览量
2023-07-27 上传
157 浏览量
185 浏览量
105 浏览量
141 浏览量
186 浏览量
197 浏览量
169 浏览量
2022-08-04 上传
119 浏览量
2023-09-26 上传
资源评论

- #完美解决问题
- #运行顺畅
- #内容详尽
- #全网独家
- #注释完整
老许的花开
- 粉丝: 34
- 资源: 328
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 昆仑通态MCGS与3台欧姆龙E5*C温控器通讯程序功能:通过昆仑通态触摸屏,实现对3台欧姆龙E5CC温控器 设定温度值,读取实际温度,设定报警值,设定报警类型,报警上下限功能 反应灵敏,通讯稳定可靠
- 大电流电动工具,电动螺丝刀,电锯批量方案,12V,30A FOC控制
- 三菱FX3G两轴标准程序,XZ两轴,包含轴点动,回零,相对与绝对定位,只要弄明白这个程序,就可以非常了解整个项目的程序如何去编写,从哪里开始下手,
- 昆仑通态MCGS与2台台达VFD-M变频器通讯程序实现昆仑通态触摸屏与2台台达VFD-M变频器通讯,程序稳定可靠 器件:昆仑通态TPC7062KD触摸屏,2台台达VFD-M变频器,附送接线说明和设置说
- MATLAB代码:考虑安全约束及热备用的电力系统机组组合研究 关键词:机组组合 直流潮流 优化调度 参考文档:店主自编文档,模型数据清晰明了 仿真平台:MATLAB+CPLEX gurobi平台
- c#上位案例,动态添加控件 1、这是个上位机案例,自己写来通过电脑监控kuka机器人信号的工具; 3、软件界面上可以动态添加要监控的信号,可以强制输出信号 4、有c#源代码,可以作为上位机与机器人通
- 三菱FX3U与力士乐VFC-x610变频器通讯程序三菱FX3U与力士乐VFC-x610变频器通讯案例程序,有注释 并附送程序,有接线方式,设置 器件:三菱FX3U的PLC,力士乐VFCx610变频
- 台达DVP PLC与3台力士乐VFC-x610变频器通讯程序 程序带注释,并附送昆仑通态程序,有接线方式,设置 器件:台达DVP ES系列的PLC,3台力士乐VFC-x610系列变频器,昆仑通态 功
- FPGA开发:实现数码管+1602双通道秒表(联系后留邮)按键切秒表模式,所用开发板DE2-115,代码可移植,内含FPGA驱动1602代码,代码有详细注释
- 汇川PLC AM403-CPU1608TN,2020产品基于CODESYS平台二次订制软件,支持16轴ethercat总线,自带以太网 USB CANOPEN 2路485,16高速输入8高速输出,功能
- 电力电子、电机驱动、数字滤波器matlab simulink仿真模型实现及相关算法的C代码实现 配置C2000 DSP ADC DAC PWM定时器 中断等模块,提供simulink与DSP的联合仿
- labview.通用OCR识别技术
- FoobarCon_v0.9.91.0.apk
- 华为HarmonyOS应用开发者高级认证,官方专业证书
- 华为HarmonyOS应用开发者高级认证,官方专业证书
- 51单片机四层电梯控制器 基于51单片机的四层电梯控制系统 包括源代码和proteus仿真 系统硬件由51单片机最小系统、蜂鸣器电路、指示灯电路、内部按键电路、外部按键电路、步进电机、ULN2003
安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功










