异或门和全加器最简结构设计原理1

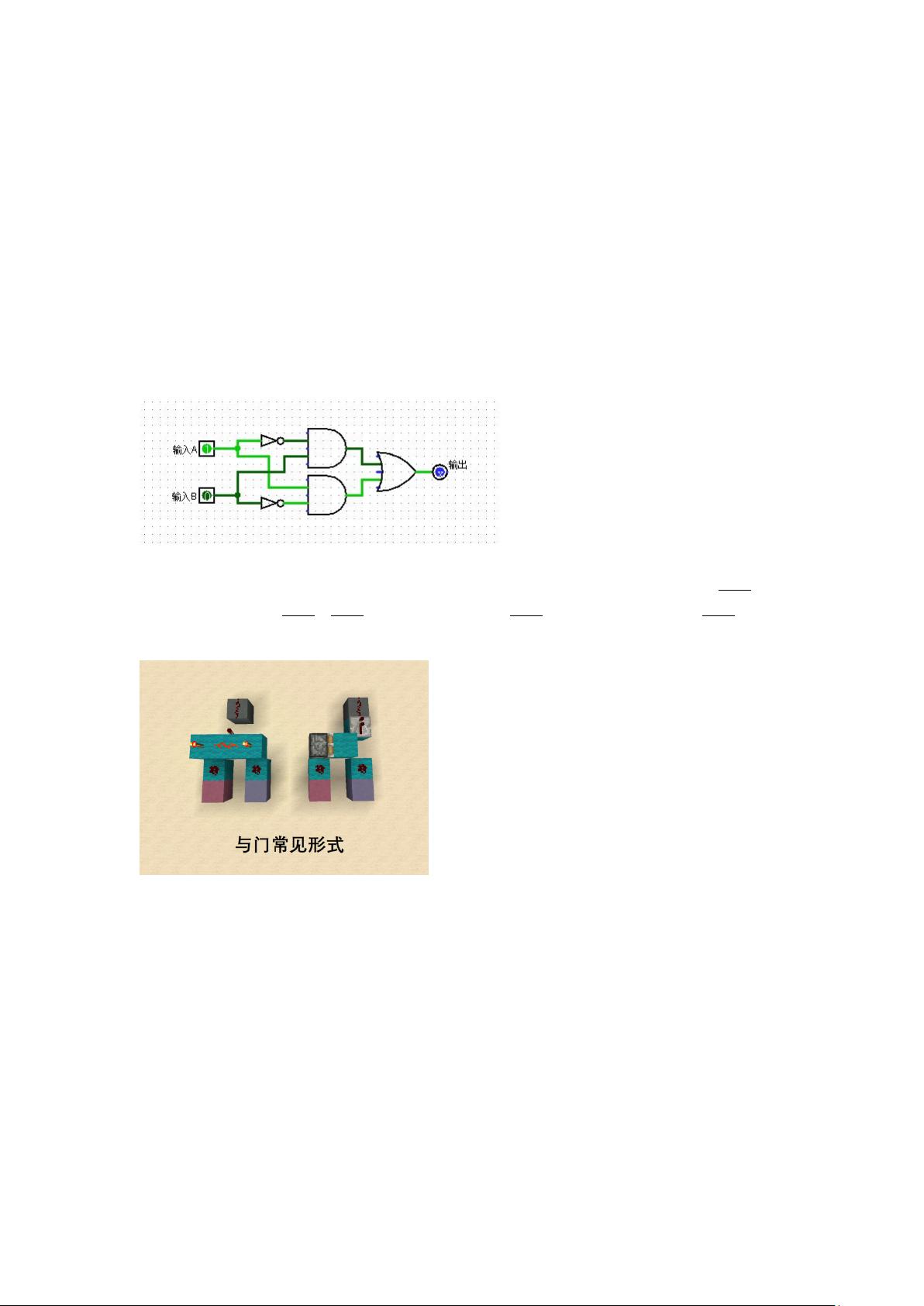
在电子电路设计中，异或门（XOR Gate）和全加器（Full Adder）是构建数字逻辑系统的基础组件。本文将详细讲解这两种门电路的最简结构设计原理，特别是针对游戏环境中的实现。 异或门是数字逻辑中的基本逻辑门，它的功能是对两个输入信号进行异或操作，即当且仅当输入信号不同时，输出为1，否则输出为0。最简单的异或门表达式是A⊕B = A·B’+B·A’，但在这个特定的游戏环境中，由于与门（AND Gate）需要通过或门（OR Gate）和非门（NOT Gate）组合而成，导致这种结构占用空间较大。因此，我们需要寻找更紧凑的表达式来实现异或门。 文章中列举了四种异或门的等价表达式，包括表达式2至5。经过逻辑运算的转换，可以证明这些表达式与原始表达式等价。表达式4（A⊕B = (A’+A·B)’+(B’+A·B)’）和表达式5（A⊕B = (A·B+A’·B’)’）在实际电路实现时，可以有效地减少空间占用。尤其是表达式4，由于其内部的A·B部分可以共用，只需一个与门。而表达式5虽然也需要两个与门，但通过巧妙利用粘性活塞的特性，可以构建紧凑的双与门结构。然而，粘性活塞在高频信号下可能会出现错误，因此，基于表达式4的异构体（型号1和型号3）是体积最小且运行最稳定的异或门设计。 全加器是数字加法电路中的关键组件，负责处理两位二进制数的本位相加以及与上一级进位的相加。全加器的输出包括本位输出（A⊕B⊕C）和进位输出（A·B+(A⊕B)·C）。在红石电路中，全加器的体积可以通过巧妙布局来压缩。例如，两个异或门并排放置，它们之间的空隙可以用于处理进位端的运算，同时避免额外构建与门。此外，全加器的进位端利用异或门中的与门结构，进一步减小了体积。在所有异构体中，基于表达式4的型号1最适合用于级联的全加器，因为它具有最小的体积，利用了两个异或门之间的空间高效布局。 了解和掌握异或门和全加器的最简结构设计，对于在游戏环境中构建复杂的数字电路至关重要。这种对电路的精细化设计不仅提升了设计的乐趣，也对构建大规模电路时的体积控制和性能优化有着深远影响。通过对各种异构体的测试和分析，我们可以更好地理解和运用这些基础逻辑门，从而创造出更高效、更可靠的电路系统。